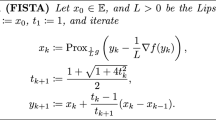Skip to main content
SpringerLink
Log in

Some modified fast iterative shrinkage thresholding algorithms with a new adaptive non-monotone stepsize strategy for nonsmooth and convex minimization problems

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

The “ fast iterative shrinkage-thresholding algorithm " (FISTA) is one of the most famous first order optimization schemes, and the stepsize, which plays an important role in theoretical analysis and numerical experiment, is always determined by a constant relating to the Lipschitz constant or by a backtracking strategy. In this paper, we design a new adaptive non-monotone stepsize strategy (NMS), which allows the stepsize to increase monotonically after finite iterations. It is remarkable that NMS can be successfully implemented without knowing the Lipschitz constant or without backtracking. And the additional cost of NMS is less than the cost of some existing backtracking strategies. For using NMS to the original FISTA (FISTA_NMS) and the modified FISTA (MFISTA_NMS), we show that the convergence results stay the same. Moreover, under the error bound condition, we show that FISTA_NMS achieves the rate of convergence to \(o\left( {\frac{1}{{{k^6}}}} \right) \) and MFISTA_NMS enjoys the convergence rate related to the value of parameter of \(t_k\), that is \(o\left( {\frac{1}{{{k^{2\left( {a + 1} \right) }}}}} \right) ;\) and the iterates generated by the above two algorithms are convergent. In addition, by taking advantage of the restart technique to accelerate the above two methods, we establish the linear convergences of the function values and iterates under the error bound condition. We conduct some numerical experiments to examine the effectiveness of the proposed algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

  1. Attouch, H., Peypouquet, J.: The rate of convergence of Nesterov’s accelerated forwardbackward method is actually faster than \( {\frac{1}{{{k^2}}}} \). SIAM J. Optim. 26, 1824–1834 (2016)

    Article  MathSciNet  Google Scholar 

  2. Attouch, H., Cabot, A.: Convergence rates of inertial forward-backward algorithms. SIAM J. Optim. 28, 849–874 (2018)

    Article  MathSciNet  Google Scholar 

  3. Apidopoulos, V., Aujol, J., Dossal, C.: Convergence rate of inertial Forward–Backward algorithm beyond Nesterov’s rule. Math. Program. 180, 137–156 (2020)

    Article  MathSciNet  Google Scholar 

  4. Beck, A., Teboulle, M.: A linearly convergent dual-based gradient projection algorithm for quadratically constrained convex minimization. Math. Oper. Res. 31, 398–417 (2006)

    Article  MathSciNet  Google Scholar 

  5. Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 183–202 (2009)

    Article  MathSciNet  Google Scholar 

  6. Becker, S.R., Candès, E.J., Grant, M.C.: Templates for convex cone problems with applications to sparse signal recovery. Math. Prog. Comp. 3, 165–218 (2011)

    Article  MathSciNet  Google Scholar 

  7. Bello, C., Jose, Y., Nghia, T.T.A.: On the convergence of the forward-backward splitting method with linesearches. Optim. Method Softw. 31, 1209–1238 (2016)

    Article  MathSciNet  Google Scholar 

  8. Chambolle, A.: An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 20, 89–97 (2004)

    Article  MathSciNet  Google Scholar 

  9. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 4, 1168–1200 (2005)

    Article  MathSciNet  Google Scholar 

  10. Chang, C.C., Lin, C.J.: LIBSVM: a library for support vector machines. ACM. Trans. Intell. Syst. Technol. 2, 1–27 (2011)

    Article  Google Scholar 

  11. Combettes, P.L., Pesquet, J.C.: Proximal splitting methods in signal processing. In: Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer, New York (2011)

  12. Chambolle, A., Dossal, C.: On the convergence of the iterates of the fast iterative shrinkage-thresholding algorithm. J. Optim. Theory Appl. 166, 968–982 (2015)

    Article  MathSciNet  Google Scholar 

  13. Donoho, D.L.: Compressed sensing. IEEE Trans. Inf. Theory 52, 1289–1306 (2006)

    Article  MathSciNet  Google Scholar 

  14. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)

    Article  MathSciNet  Google Scholar 

  15. Luo, Z.Q., Tseng, P.: Error bound and the convergence analysis of matrix splitting algorithms for the affine variational inequality problem. SIAM J. Optim. 2, 43–54 (1992)

    Article  MathSciNet  Google Scholar 

  16. Luo, Z.Q.: New error bounds and their applications to convergence analysis of iterative algorithms. Math. Program. 88, 341–355 (2000)

    Article  MathSciNet  Google Scholar 

  17. Lorenz, D.A., Pock, T.: An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 51, 311–325 (2015)

    Article  MathSciNet  Google Scholar 

  18. Liang, J., Fadili, J., Peyré, G.: Convergence rates with inexact non-expansive operators. Math. Program. 159, 403–434 (2016)

    Article  MathSciNet  Google Scholar 

  19. Liu, H.W., Wang, T., Liu, Z.X.: Convergence rate of inertial forward-backward algorithms based on the local error bound condition. arXiv:2007.07432

  20. Molinari, C., Liang, J., Fadili, J.: Convergence rates of forward-douglas-rachford splitting Method. J. Optim. Theory Appl. 182, 606–639 (2019)

    Article  MathSciNet  Google Scholar 

  21. Nesterov, Y.: A method for solving the convex programming problem with convergence rate \(O\left( {\frac{1}{{{k^2}}}} \right)\). Dokl. Akad. Nauk SSSR 269, 543–547 (1983)

    MathSciNet  Google Scholar 

  22. Nesterov, Y.: Gradient methods for minimizing composite functions. Math. Program. 140, 125–161 (2013)

    Article  MathSciNet  Google Scholar 

  23. O’Donoghue, B., Candès, E.: Adaptive restart for accelerated gradient schemes. Found. Comput. Math. 15, 715–732 (2015)

    Article  MathSciNet  Google Scholar 

  24. Sra, S., Nowozin, S., Wright, S.J.: Optimization for Machine Learning. MIT Press, Cambridge (2012)

    Google Scholar 

  25. Sun, W.Y., Yuan, Y.X.: Optimization Theory and Methods: Nonlinear Programming. Springer, Berlin (2010)

    Google Scholar 

  26. Su, W., Boyd, S., Candès, E.J.: A differential equation for modeling Nesterov’s accelerated gradient method: Theory and insights. J. Mach. Learn. Res. 17, 1–43 (2016)

    MathSciNet  MATH  Google Scholar 

  27. Scheinberg, K., Goldfarb, D., Bai, X.: Fast first-order methods for composite convex optimization with backtracking. Found. Comput. Math. 14, 389–417 (2014)

    Article  MathSciNet  Google Scholar 

  28. Tseng, P.: Approximation accuracy, gradient methods, and error bound for structured convex optimization. Math. Program. 125, 263–295 (2010)

    Article  MathSciNet  Google Scholar 

  29. Tao, S., Boley, D., Zhang, S.: Local linear convergence of ISTA and FISTA on the LASSO problem. SIAM J. Optim. 26, 313–336 (2016)

    Article  MathSciNet  Google Scholar 

  30. Wen, B., Chen, X.J., Pong, T.K.: Linear convergence of proximal gradient algorithm with extrapolation for a class of nonconvex nonsmooth minimization problems. SIAM J. Optim. 27, 124–145 (2017)

    Article  MathSciNet  Google Scholar 

  31. Wright, S.J., Nowak, R.D., Figueiredo, M.A.T.: Sparse reconstruction by separable approximation. IEEE T. Signal Proces. 57, 2479–2493 (2009)

    Article  MathSciNet  Google Scholar 

  32. Wang, T., Liu, H.: Convergence results of a new monotone Inertial Forward-Backward Splitting algorithm under the local Hölder error bound condition. Appl. Math. Optim. (2022). https://doi.org/10.1007/s00245-022-09859-y

Download references

Acknowledgements

The work was supported by the National Natural Science Foundation of China (No. 11901561), the Natural Science Foundation of Guangxi (No. 2018GXNSFBA281180) and the Postdoctoral Fund Project of China (Grant No. 2019M660833), Guizhou Provincial Science and Technology Projects (No. QKHJC-ZK[2022]YB084).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xidian University, Xi’an, 710126, China

    Hongwei Liu & Ting Wang

  2. School of Mathematics and Statistics, Guizhou University, Guiyang, 550025, China

    Zexian Liu

Authors
  1. Hongwei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ting Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zexian Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ting Wang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, H., Wang, T. & Liu, Z. Some modified fast iterative shrinkage thresholding algorithms with a new adaptive non-monotone stepsize strategy for nonsmooth and convex minimization problems. Comput Optim Appl 83, 651–691 (2022). https://doi.org/10.1007/s10589-022-00396-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-022-00396-6

Keywords

Mathematics Subject Classification

Search

Navigation