Proximal primal–dual best approximation algorithm with memory

Abstract

We propose a new modified primal–dual proximal best approximation method for solving convex not necessarily differentiable optimization problems. The novelty of the method relies on introducing memory by taking into account iterates computed in previous steps in the formulas defining current iterate. To this end we consider projections onto intersections of halfspaces generated on the basis of the current as well as the previous iterates. To calculate these projections we are using recently obtained closed-form expressions for projectors onto polyhedral sets. The resulting algorithm with memory inherits strong convergence properties of the original best approximation proximal primal–dual algorithm. Additionally, we compare our algorithm with the original (non-inertial) one with the help of the so called attraction property defined below. Extensive numerical experimental results on image reconstruction problems illustrate the advantages of including memory into the original algorithm.

1 Introduction

Motivated by problems arising in the field of inverse problems, signal processing, computer vision and machine learning, there has been an increasing interest in primal–dual methods [12, 32, 33]. Over the last years, substantial progress has been made. Among others, the recent advances concern block algorithms [18, 24], asynchronous methods [21, 43], generalizations of projection algorithms [22, 28] and introduction of memory effect.

While versions with memory of several proximal primal–dual algorithms already exist [16, 17, 34, 41, 46], in this paper we propose a new way of introducing memory effect in projection algorithms by studying algorithm [2]. We consider the following convex optimization problem

$$\begin{aligned} \min \limits _{p\in H}\ f(p)+g(Lp), \end{aligned}$$

(1)

where H and G are two real Hilbert spaces, $f\,{:}\,H \rightarrow {\mathbb {R}}\cup \{+\infty \}, g\,{:}\,G\rightarrow {\mathbb {R}}\cup \{+\infty \}$ are proper convex lower semi-continuous functions and $L\,{:}\,H\rightarrow G$ is a bounded linear operator. Under suitable regularity conditions problem (1) is equivalent to the problem of finding $p \in H$ such that

$$\begin{aligned} 0 \in \partial \, f (p)+L^{*}\partial \, g(Lp), \end{aligned}$$

(2)

where $\partial (\cdot )$ denotes the subdifferential set-valued operator. Problem (2) is of the form

$$\begin{aligned} 0 \in A(p)+L^{*}B(Lp), \end{aligned}$$

(P)

where $A\,{:}\,H\rightrightarrows H$ and $B\,{:}\,G\rightrightarrows G$ are maximally monotone set-valued operators.

Different approaches to solve (P) have been proposed e.g. in [5, 26, 48]. In particular, primal–dual approaches to solve (1) may lead to formulations which can be represented as in (P), see e.g. [1, 2, 9, 10, 13, 15, 23] and the references therein. Recently, the primal–dual approach has been applied in [54] to a more general form of (P) involving the sum of two maximally monotone operators and a monotone operator. The case when A is maximal monotone and B is strongly monotone was considered in [48]. The overview of primal–dual approaches to solve (P) has been recently proposed in [32].

Some algorithms to solve (1) which rely on including $x_{n-1}$ into the definition of $x_{n+1}$ were proposed in [3, 4, 9, 15, 30, 31, 35,36,37,38,39, 41, 42]. They are mostly based on discretizations of the second order differential system related to the problem (2). This system, called heavy ball with friction, is exploited in order to accelerate convergence. Indeed, the introduction of the inertial term was shown to improve the speed of convergence significantly [30, 31].

In [46] Pesquet and Pustelnik proposed a primal method to solve (1) with inertial effect introduced through inertia parameters. The method explores information from more than one previous steps and allows finding zeros of the sum of an arbitrary finite number of maximally monotone operators (see also [26]).

For monotone inclusion problems (P) inertial proximal algorithms and fixed-points iterations have been proposed in [3, 4, 8, 9, 11, 34, 39, 40, 48].

In the present paper we propose a new projection algorithm with memory. We introduce a memory effect into projection algorithms by relying on successive projections onto polyhedral sets constructed with the help of halfspaces originating from current and previous iterates. To the best of our knowledge this way of introducing memory has not been considered yet.

By applying to problem (P) the generalized Fenchel–Rockafellar duality framework [44, Corollary 2.12] (see also Corollary 2.4 of [45]) we obtain the dual inclusion problem which amounts to finding $v^*\in G$ such that

$$\begin{aligned} 0 \in -LA^{-1}(-Lv^*)+B^{-1}v^*. \end{aligned}$$

(D)

By [44, Corollary 2.12], a point $p\in H$ solves (P) if and only if $v^*\in G$ solves (D) and $(p,v^*)\in Z$, where

$$\begin{aligned} Z:=\{ (p,v^*)\in H\times G \ |\ -L^* v^* \in Ap \quad \text {and}\quad Lp \in B^{-1}v^* \}. \end{aligned}$$

(3)

In the case when $L=Id$ and $H=G$, the set Z reduces to the extended solution set $S_{e}(A,B)$ as defined in [25]. The set Z is a closed convex subset of $H\times G$ (see e.g. [7, Proposition 23.39]).

The Fenchel–Rockafellar dual problem of (1) takes the form (see [45])

$$\begin{aligned} \min _{v^*\in G}\ f^*(-L^*v^*)+g^*(v^*), \end{aligned}$$

(4)

where $f^*$ denotes the conjugate function [47]. In this case set Z is of the form

$$\begin{aligned} Z = \{(p,v^*)\in H\times G \ |\ -Lv^* \in \partial f(x)\ \text {and}\ v^*\in \partial g(Lx) \}. \end{aligned}$$

(5)

1.1 Projection methods

The idea of finding a point in Z is based on the fact that

$$\begin{aligned} Z \subset \{ (p,v^*)\in H \times G \ |\ \varphi (p,v^*) \le 0 \}:=H_\varphi , \end{aligned}$$

where $\varphi (p,v^*):=\langle p - a \ |\ a^*+L^*v^* \rangle + \langle b^*-v^* \ |\ Lp - b \rangle , (a,a^*)\in \text {graph}A, (b,b^*)\in \text {graph}B$. This suggests the following iterative scheme for finding a point in Z based on projections onto $H_\varphi$: for any $(p_0,v_0^*)\in H\times G$ and relaxation parameters $\lambda _n\in (0,2), n\in {\mathbb {N}}$ let

$$\begin{aligned} \left( p_{n+1},v_{n+1}^*\right) :=(p_n,v_n)+\lambda _n \left( P_{H_n}(p_n,v_n^*)-\left( p_n,v_n^*\right) \right) , \end{aligned}$$

(6)

where $H_n:=\{ (p_n,v_n^*)\in H \times G \ |\ \varphi (p_n,v_n^*) \le 0 \}$ with $\varphi _n$ defined for suitably chosen $(a_n,a_n^*)\in \text {graph}A, (b_n,b_n^*)\in \text {graph}B$ ([1, Proposition 2.3], see also [25, Lemma 3]) and $P_D(x)$ denoting the projection of x onto the set D. For $L=Id$ this iteration scheme has been proposed by Eckstein and Svaiter [25] and its fundamental convergence properties has been investigated in [25, Proposition 1, Proposition 2].

Further convergence properties of (6) have been investigated in [1] and [6, Theorem 2]. The sequence generated by (6) is Fejér monotone with respect to set Z and, in general, only its weak convergence is guaranteed.

Modifications of (6) to force strong convergence have been proposed in [2, 51, 52, 54, 56]. Recently, asynchronous block-iterative methods are proposed in [21, 24].

1.2 The aim

In the present paper we propose a primal–dual projection algorithm with memory to solve (P) which relies on finding a point in the set Z defined by (3). The origin of our idea goes back to the algorithm of Haugazeau [7, Corollary 29.8], who proposed an algorithm for finding the projection of $x_0\in H$ onto the intersection of a finite number of closed convex sets by using projections of $x_0$ onto intersections of two halfspaces. These halfspaces are defined on the basis of the current iterate $x_n$ (see also [51,52,53]).

In our approach we take into account projections of $x_0$ onto intersections of three halfspaces which are defined on the basis of not only $x_n$ but also $x_{n-1}$.

The contribution of the paper is as follows.

• We apply formulas for projections onto intersections of three half-spaces in Hilbert spaces derived in [50]. We show that in the considered cases (Proposition 4) the complete enumeration is not required (Proposition 5).

• We propose a number of iterative schemes with memory for solving primal–dual problems defined by (P) and (D).

• We apply our iterative schemes to propose a proximal algorithm with memory to solve minimization problem defined by a finite sum of convex functions.

• We provide convergence comparison of the proposed algorithm with its non-memory version in terms of attraction property (Proposition 7).

• We perform an experimental study aiming at comparing the best approximation algorithm proposed in [2] and our algorithm.

The organization of the paper is as follows. In Sect. 2 we propose the underlying iterative schemes with memory and we formulate basic convergence results. In Sect. 3 we provide several versions of the iterative scheme with memory. One of the main ingredients is a closed-form formula for projectors onto polyhedral sets introduced in [50]. In Sect. 4 we perform the convergence comparison of the proposed iterative schemes. In Sect. 5 we cast our general idea so as to be able to solve optimization problem of minimization of the sum of two convex, not necessarily differentiable functions. In Sect. 6 we present the results of the numerical experiment.

2 The proposed approach

In Sect. 2.1 we recall generic Fejér Approximation Scheme for finding an element from the set Z defined by (3) and its basic properties. In Sect. 2.2 we propose refinements of Fejér Approximation Scheme which are based on the idea proposed by Haugazeau [27], see also [7, Corollary]. The crucial issue of the proposed refinements is to improve convergence properties.

In the sequel, for any $x \in H\times G$ we write $x = \left( p,v^*\right)$, where $p\in H$ and $v^*\in G$.

2.1 Successive Fejér approximations iterative scheme

Let H, G be real Hilbert spaces and let Z be defined by (3). Let $\{H_n\}_{n\in {\mathbb {N}}}\subset H\times G$, be a sequence of convex closed sets such that $Z\subset H_n,\ n\in {\mathbb {N}}$. The projections of any $x\in H$ onto $H_n$ are uniquely defined.

Theorem 1

([1, Proposition 3.1], see also [20]) For any sequence generated by Iterative Scheme 1 the following hold:

• 1. $\{x_n\}_{n\in {\mathbb {N}}}\subset H\times G$ is Fejér monotone with respect to the set Z, i.e.

  $$\begin{aligned} \forall _{n\in {\mathbb {N}}} \ \forall _{z\in Z}\ \Vert x_{n+1}-z\Vert \le \Vert x_n-z\Vert , \end{aligned}$$

• 2. $\sum \nolimits _{n=0}^{+\infty } \lambda _n (2-\lambda _n) \Vert P_{H_n}(x_{n})-x_n\Vert ^2< +\infty$,

• 3. if

  $$\begin{aligned} \forall x\in H\times G \ \forall \{k_n\}_{n\in {\mathbb {N}}}\subset {\mathbb {N}} \quad x_{k_n} \rightharpoonup x \implies x \in Z, \end{aligned}$$

  then $\{x_{n}\}_{n\in {\mathbb {N}}}$ converges weakly to a point in Z.

In [1] the sets $H_n$ appearing in Iterative Scheme 1 are defined as closed halfspaces $H_{a_n,b_n^*}$,

$$\begin{aligned} \begin{aligned} H_{a_n,b_n^*}&:= \left\{ x \in H\times G \mid \left\langle x \mid s_{a_n,b_n^*}^*\right\rangle \le \eta _{a_n,b_n^*} \right\} ,\\ s_{a_n,b_n^*}^*&:= \left( a_n^* + L^*b_n^*, b_n - La_n\right) , \\ \eta _{a_n,b_n^*}&:=\left\langle a_n \mid a_n^* \right\rangle + \left\langle b_n \mid b_n^* \right\rangle , \end{aligned} \end{aligned}$$

(7)

with

$$\begin{aligned} \begin{aligned}&a_n := J_{\gamma _n A} \left( p_n - \gamma _n L^* v_n^*\right) ,\quad b_n := J_{\mu _n B} \left( L p_n + \mu _n v_n^*\right) , \\&a_n^* := \gamma _n^{-1}(p_n-a_n) - L^* v_n^*,\quad b_n^* := \mu _n^{-1} (Lp_n-b_n) + v_n^*, \end{aligned} \end{aligned}$$

where for any maximally monotone operator D and constant $\xi >0, J_{\xi D}(x)=(Id+\xi D)^{-1}(x)$. Parameters $\mu _n,\gamma _n>0$ are suitable defined. It easy to see $H_{\varphi _n}=H_{a_n,b_n^*}$, where $\varphi _n=\varphi (a_n,b_n^*)$.

For $H_n=H_{a_n,b_n^*}$ Theorem 1 can be strengthened in following way.

Theorem 2

[1, Proposition 3.5] For any sequence generated by Iterative Scheme 1 with $H_n$ defined by (7) the following hold:

• 1. $\{x_{n}\}_{n\in {\mathbb {N}}}=\{(p_n,v_n^*)\}_{n\in {\mathbb {N}}}$ is Fejér monotone with respect to the set Z,

• 2. $\sum \nolimits _{n=0}^{+\infty } \Vert a_n^*+L^*b_n^*\Vert ^2 < +\infty$ and $\sum \nolimits _{n=0}^{+\infty } \Vert La_n-b_n\Vert ^2 < +\infty$,

• 3. $\sum \nolimits _{n=0}^{+\infty } \Vert p_{n+1}-p_n\Vert ^2 < +\infty$ and $\sum \nolimits _{n=0}^{+\infty } \Vert v_{n+1}^*-v_n^*\Vert ^2 < +\infty$,

• 4. $\sum \nolimits _{n=0}^{+\infty } \Vert p_n-a_n\Vert ^2 < +\infty$ and $\sum \nolimits _{n=0}^{+\infty } \Vert v_n^*-b_n^*\Vert ^2 < +\infty$,

• 5. $\{x_{n}\}_{n\in {\mathbb {N}}}$ converges weakly to a point in Z.

2.2 Best approximation iterative schemes

Here we study iterative best approximation schemes in the form of Iterative Scheme 2. For any $x,y\in H\times G$ we define

$$\begin{aligned} H(x,y):=\{h\in H\times G\ |\ \langle h-y \ |\ x-y\rangle \le 0 \}. \end{aligned}$$

As previously, let $\{H_n\}_{n\in {\mathbb {N}}}\subset H\times G$ be a sequence of closed convex sets, $Z\subset H_n$ for $n\in {\mathbb {N}}$.

The choice of $C_n = H(x_n,x_{n+1/2})$ has been already investigated in [2]. There it has been shown that this choice allows to achieve strong convergence of the constructed sequence $\{x_{n}\}_{n\in {\mathbb {N}}}$ under relatively mild conditions.

Our aim is to propose and investigate other choices of $C_n$ defined with the help of not only $x_{n},\ x_{n+1/2}$ but also $x_{n-1}$ and/or $x_{n-1+1/2}$. For such choices of $C_n$ with memory the Iterative scheme 2 becomes an iterative scheme with memory, i.e. in the construction of the next iterate $x_{n+1}$ not only current iterate $x_n$ but also $x_{n-1}$ is taken into account. In the sequel we refer to the Iterative Scheme 2 with $C_{n}= H(x_n,x_{n+1/2})$ as a scheme without memory and we compare it with Iterative Scheme 2, where $C_{n}$ are with memory (see Proposition 4 below).

The Fejérian step in Iterative Scheme 2 coincides with what has been defined in Iterative Scheme 1 and was previously discussed in [1, 20].

Convergence properties of sequences $\{x_n\}_{n\in {\mathbb {N}}}$ generated by Iterative Scheme 2 are summarized in Proposition 1 based on Proposition 2.1. of [2] which, in turn, is based on Proposition 3.1. of [19].

Proposition 1

Let $Z$ be a nonempty closed convex subset of $H\times G$ and let $x_0=(p_0,v_0^*) \in H\times G$. Let $\{C_n\}_{n\in {\mathbb {N}}}$ be any sequence satisfying $Z\subset C_n\subset H(x_{n},x_{n+1/2}), n\in {\mathbb {N}}$. For the sequence $\{x_n\}_{n \in {\mathbb {N}}}$ generated by Iterative Scheme 2 the following hold:

• 1. $Z\subset H(x_0,x_n) \cap C_n$ for $n\in {\mathbb {N}}$,

• 2. $\Vert x_{n+1}-x_0\Vert \ge \Vert x_n-x_0\Vert$ for $n\in {\mathbb {N}}$,

• 3. $\sum \nolimits _{n=0}^{+\infty }\Vert x_{n+1}-x_n\Vert ^2<+\infty$,

• 4. $\sum \nolimits _{n=0}^{+\infty }\Vert x_{n+1/2}-x_n\Vert ^2<+\infty$.

• 5. If

  $$\begin{aligned} \forall x\in H\times G\ \forall \{k_n\}_{n\in {\mathbb {N}}}\subset {\mathbb {N}} \quad x_{k_n}\rightharpoonup x \implies x \in Z, \end{aligned}$$

  then $x_n\rightarrow P_Z(x_0)$.

Proof

The proof follows the lines of the proof of Proposition 2.1 of [2]. The proof of assertion 3 and 5 coincide with the respective parts of the proof of Proposition 2.1 of [2] and is omitted here. We provide the proofs of assertions 1, 2, 4 for completeness.

• 1. First we show that $Z\subset H(x_0,x_n)$. For $n=0, x_{1}=P_{H(x_0,x_0)\cap C_0}(x_0)$, so $Z\subset H(x_0,x_1)$. Furthermore, $H(x_0,x_n)\cap C_n \subset H(x_0,P_{H(x_0,x_n) \cap C_n}(x_0))$ and

  $$\begin{aligned} Z\subset H(x_0,x_n)&\implies Z\subset H(x_0,x_n) \cap C_n\\&\implies Z\subset H(x_0,P_{H(x_0,x_n)\cap C_n}(x_0))\\&\Leftrightarrow Z\subset H(x_0,x_{n+1}) \end{aligned}$$

• 2. By construction, for $n\in {\mathbb {N}}, x_{n+1}=P_{H(x_0,x_{n})\cap C_n}(x_0)$ and $x_{n+1}\subset H(x_0,x_n) \cap C_n$, so $x_{n+1}\in H(x_0,x_n)$. This implies $\Vert x_n-x_0\Vert \le \Vert x_{n+1}-x_0\Vert$.

• 4. $C_n \subset H(x_n,P_{C_n}(x_n))\subset H(x_n, x_n+\lambda _n (P_{C_n}(x_n)-x_n)) = H(x_n,x_{n+1/2})$. Since $x_{n+1}\in C_n \subset H_n \subset H(x_n,x_{n+1/2})$, we deduce that

  $$\begin{aligned}&\Vert x_{n+1/2}-x_n\Vert ^2\le x_{n+1}-x_{n+1/2}\Vert ^2+\Vert x_{n+1/2}-x_n\Vert ^2\\&\quad \le x_{n+1}-x_{n+1/2}\Vert ^2+2\langle x_{n+1}-x_{n+1/2} \ |\ x_{n+1/2}-x_{n}\rangle +\Vert x_{n+1/2}-x_n\Vert ^2\\&\quad \le \Vert x_{n+1}-x_n\Vert ^2. \end{aligned}$$

  By item 3, $\sum \nolimits _{n=0}^{+\infty } \Vert x_{n+1}-x_n\Vert ^2< +\infty$, hence $\sum \nolimits _{n=0}^{+\infty } \Vert x_{n+1/2}-x_n\Vert ^2 < +\infty$.

$\square$

Remark 1

Note that for $C_n=H(x_n,x_{n+1/2})$ and $H_n=H_{a_n,b_n^{*}}$ we obtain the primal–dual best approximation algorithm introduced by Alotaibi et al. in [2], involving projections onto the intersections of two halfspaces $H(x_{0},x_{n})\cap H(x_n,x_{n+1/2})$ studied in [7, Section 28.3]. Condition $Z\subset C_n\subset H(x_{n},x_{n+1/2}), n\in {\mathbb {N}}$ allows one to consider choices of $C_{n}$ other than $C_n=H(x_n,x_{n+1/2})$.

When $H_n:=H_{a_n,b_n^{*}} n\in {\mathbb {N}}$, where $H_{a_n,b_n^{*}}$ are defined by (7), Proposition 1 takes the following form.

Proposition 2

Let $Z$ be a nonempty closed convex subset of $H\times G$ and let $x_0=(p_0,v_0^*) \in H\times G$. Let $\{C_n\}_{n\in {\mathbb {N}}}$ be a sequence of closed convex sets satisfying the condition $Z\subset C_n\subset H(x_{n},x_{n+1/2})$ and $H_n:=H_{a_n,b_n^{*}}, \in {\mathbb {N}}$. For any sequence $\{x_n\}_{n \in {\mathbb {N}}}$ generated by Iterative Scheme 2 the following hold:

• 1. $\Vert x_{n+1}-x_0\Vert \ge \Vert x_n-x_0\Vert$ for all $n\in {\mathbb {N}}$,

• 2. $\sum \nolimits _{n=0}^{+\infty } \Vert p_{n+1}-p_n\Vert ^2 <+\infty$ and $\sum \nolimits _{n=0}^{+\infty } \Vert v_{n+1}^*-v_n^*\Vert ^2 <+\infty$,

• 3. $\sum \nolimits _{n=0}^{+\infty } \Vert p_n-a_n\Vert ^2 < +\infty$ and $\sum \nolimits _{n=0}^{+\infty } \Vert Lp_n-b_n\Vert ^2 < +\infty$,

• 4. $p_n\rightarrow {\bar{x}}, v_n^*\rightarrow {\bar{v}}^*$ and $({\bar{p}},{\bar{v}}^*)\in Z$.

Proof

• 1. The statement follows directly from item 2 of Proposition 1.

• 2. By Proposition 1,

  $$\begin{aligned} \sum \limits _{n=0}^{+\infty } \Vert p_{n+1}-p_n\Vert ^2+\sum \limits _{n=0}^{+\infty } \Vert v_{n+1}^*-v_n^*\Vert ^2=\sum \limits _{n=0}^{+\infty }\Vert x_{n+1}-x_n\Vert ^2<+\infty . \end{aligned}$$

• 3. and 4. The proof is similar to the proof of [1, Proposition 3.5].

$\square$

Remark 2

Proposition 2 shows the importance of the condition $Z\subset C_n\subset H(x_{n},x_{n+1/2})$ in proving the strong convergence of Iterative Scheme 2.

3 The choice of $C_{n}$

One of the main contributions of the paper is to consider $C_n$ which use the information from the previous step. In this way Iterative Scheme 2 becomes a scheme with memory in the sense that the construction of $x_{n+1}$ depends not only on $x_{n+1/2},\ x_{n},$ but also on $x_{n-1+1/2},\ x_{n-1}$.

We start with the following propositions.

Proposition 3

Let $x,u,v\in H$. Then $H(x,u)\cap H(x,v)\subset H(x,\tau u + (1-\tau )v)$ for all $\tau \in [0,1]$.

Proof

Let $h\in H(x,u)\cap H(x,v)$, i.e.

$$\begin{aligned} \langle h-u \ |\ x - u\rangle \le 0 \quad \text {and} \quad \langle h-v \ |\ x - v\rangle \le 0. \end{aligned}$$

For any $\tau \in [0,1]$ we have

$$\begin{aligned}&\langle h - \tau v - (1-\tau )w \ |\ x-\tau v - (1-\tau )w \rangle \\&\quad = \langle h \ |\ x \rangle - \tau \langle h \ |\ v \rangle - \tau \langle v \ |\ x \rangle - (1-\tau ) \langle h \ |\ w \rangle - (1-\tau ) \langle w \ |\ x \rangle \\&\qquad + \tau ^2 \langle v \ |\ v \rangle +(1-\tau )^2 \langle w \ |\ w \rangle +2\tau (1-\tau )\langle v \ |\ w\rangle \\&\quad = \tau \langle h \ |\ x \rangle - \tau \langle h \ |\ v \rangle - \tau \langle v \ |\ x \rangle + \tau \langle v \ |\ v \rangle \\&\qquad +(1-\tau ) \langle h \ |\ x \rangle - (1-\tau ) \langle h \ |\ w \rangle - (1-\tau ) \langle w \ |\ x \rangle + (1-\tau ) \langle w \ |\ w \rangle \\&\qquad + \tau ^2 \langle v \ |\ v\rangle + (1-\tau )^2 \langle w \ |\ w\rangle + 2 \tau (1-\tau ) \langle v \ |\ w \rangle - \tau \langle v \ |\ v \rangle - (1-\tau )\langle w \ |\ w \rangle \\&\quad \le \tau ^2 \langle v \ |\ v\rangle + (1-\tau )^2 \langle w \ |\ w\rangle + 2 \tau (1-\tau ) \langle v \ |\ w \rangle - \tau \langle v \ |\ v \rangle - (1-\tau )\langle w \ |\ w \rangle \\&\quad = \tau (\tau - 1) \langle v \ |\ v\rangle + (1-\tau )(-\tau ) \langle w \ |\ w \rangle + 2\tau (1-\tau ) \langle v \ |\ w \rangle \\&\quad \le \tau (\tau - 1) \Vert v\Vert ^2 + (1-\tau )(-\tau ) \Vert w\Vert ^2 + 2 \tau (1-\tau ) \Vert v\Vert \Vert w\Vert \\&\quad = \tau (\tau -1) (\Vert v\Vert ^2 -2 \Vert v\Vert \Vert w\Vert + \Vert w\Vert ^2)= - \tau (1-\tau ) (\Vert v\Vert +\Vert w\Vert )^2\le 0. \end{aligned}$$

Thus $h \in H(x,\tau u + (1-\tau )v)$. $\square$

The following proposition provides examples of sets $C_{n}$ with memory satisfying requirements of Proposition 2 (see Remark 2).

Proposition 4

For $C_n$ defined as

$$\begin{aligned} C_n&:= H(x_n, x_{n+\frac{1}{2}}) \cap H(x_{n-1}, x_{n-\frac{1}{2}})\ \text {for}\ n\ge 1 \ \text {and} \ C_0=H(x_0,x_{1/2}), \end{aligned}$$

(8)

$$\begin{aligned} C_n&:= H(x_n, x_{n+\frac{1}{2}}) \cap H(x_{0}, x_{n-1}) \ \text {for} \ n\ge 1 \ \text {and} \ C_0=H(x_0,x_{1/2}), \end{aligned}$$

(9)

$$\begin{aligned} C_n&:= H(x_n, x_{n+\frac{1}{2}}) \cap H(x_0, \tau _n x_n + (1-\tau _n) x_{n-1})) \ \text {for}\ \tau _n \in (0,1), n\ge 1 \nonumber \\&\quad \text {and}\,C_0=H(x_0,x_{1/2}) \end{aligned}$$

(10)

the assertions 1–5 of Proposition 1 holds.

Proof

To apply Proposition 1 we need only to show that $C_n$ are closed and convex and $Z\subset C_n\subset H_n$. The sets $C_n$ are closed and convex as intersections of finitely many closed halfspaces. By construction of $x_{n+1/2}$ we have $Z\subset H(x_n,x_{n+1/2})$ for all $n \in {\mathbb {N}}$.

• 1. For $C_n$ given by (8) we have $Z \subset H(x_n,x_{n+1/2})\cap H(x_{n-1},x_{n-1+1/2})$ since $Z\subset H(x_n,x_{n+1/2})$.

• 2. Let $C_n$ be given by (9). By construction, $Z\subset H(x_0,x_{1/2})=H(x_0,x_1)=C_0$. Let $n \in {\mathbb {N}}$ and suppose $Z\subset C_k=H(x_{k},x_{k+1/2})\cap H(x_{0},x_{k-1})$ for all $1\le k\le n$. We have

  $$\begin{aligned}&Z\subset H(x_0,x_{n-1})\cap H(x_{n-1},x_{n-1+1/2})\cap H(x_{0},x_{n-2})= C_{n}\cap H(x_{0},x_{n-2})\\&\implies Z \subset H(x_0,P_{C_{n}\cap H(x_{0},x_{n-2})}(x_0))\\&\Leftrightarrow Z \subset H(x_0,x_n) \Leftrightarrow Z \subset H(x_0,x_n)\cap H(x_{n+1},x_{n+1+1/2})=C_{n+1}. \end{aligned}$$

  By induction, $Z\subset C_n$ for all $n\ge 0$.

• 3. Let $C_n$ be given by (10). By construction, $Z\subset H(x_0,x_{1/2})=H(x_0,x_1)=C_0$. By Proposition 3, we have

  $$\begin{aligned}&Z\subset H(x_0,x_n) \cap H(x_0,x_{n-1}) \\&\implies Z \subset H(x_0,\tau _n x_n + (1-\tau _n)x_{n-1})\ \text {for all}\ \tau _n \in (0,1). \end{aligned}$$

  Let $n \in {\mathbb {N}}$ and suppose $Z\subset C_k=H(x_{k},x_{k+1/2})\cap H(x_{0},x_{k-1})$ and $Z\subset H(x_0,x_k)$ for all $1\le k\le n$. Then

  $$\begin{aligned}&Z \subset C_n = H(x_n, x_{n+1/2}) \cap H(x_0, \tau _n x_n + (1-\tau _n) x_{n-1}))\\&\implies Z \subset H(x_n, x_{n+1/2}) \cap H(x_0, \tau _n x_n + (1-\tau _n) x_{n-1})) \cap H(x_0,x_n)\\&\implies Z\subset H(x_0,P_{H(x_0,H(x_n, x_{n+1/2}) \cap H(x_0, \tau _n x_n + (1-\tau _n) x_{n-1})) \cap H(x_0,x_n)}(x_0))\\&\Leftrightarrow Z \subset H(x_0,P_{C_n\cap H(x_0,x_n)}(x_0)) = H(x_0,x_{n+1})\\&\Leftrightarrow Z\subset H(x_0,x_n)\cap H(x_{n+1})\implies Z \subset H(x_0,\tau _{n+1}x_{n+1}+(1-\tau _{n+1})x_n). \end{aligned}$$

  Thus $Z\subset C_n$ for all $n\in {\mathbb {N}}$.

$\square$

3.1 Closed-form expressions for projectors onto intersection of three halfspaces

In this subsection we recall the closed-form formulas for projectors onto polyhedral sets as given in [50]. These halfspaces are given in a form

$$\begin{aligned} A_i=\{h \in H\times G \ |\ \langle h \ |\ u_i\rangle \le \eta _i \},\ i=1,\ldots ,m \end{aligned}$$

(11)

where $u_i\ne 0, \eta _i\in {\mathbb {R}}, i=1,\ldots ,m, m\in {\mathbb {N}}$.

Let $w_i:=\langle x \ |\ u_i \rangle -\eta _i, i \in M:=\{1,\ldots ,m\}$ and let $G:=[\langle u_i \ |\ u_j \rangle ]_{i,j\in M}$. For any sets $I\subset M, J\subset M, I,J\ne \emptyset$ the symbol $G_{I,J}$ denote the submatrix of G composed by rows indexed by I and columns indexed by J only. Let $s_I(a):=\{ b \in I \ |\ b\le a \}$. We define

$$\begin{aligned} B_I^a:=\left\{ \begin{array}{ll} (-1)^{|s_I(a)|} &{} \quad \text {if} \quad a \in I, \\ (-1)^{|I|+1} &{} \quad \text {if} \quad a \notin I. \end{array}\right. \end{aligned}$$

Theorem 3

[50, Theorem 2] Let $m\in {\mathbb {N}}, m\ne 0$ and let $M=\{1,\ldots ,m\}$. Let $A=\bigcap \limits _{i=1}^m A_i\ne \emptyset , x\notin A$. Let $\text {rank}\ G=k$. Let $\emptyset \ne I\subset M, |I|\le k$ be such that $\det G_{I,I}\ne 0$. Let

$$\begin{aligned} \nu _i:= \left\{ \begin{array}{lcl} \sum _{j \in I} w_j B_I^{j} B_I^{i} \det G_{I\backslash j, I\backslash i} &{} \text {if} &{} |I|>1,\\ w_i &{} \text {if} &{} |I|=1 \end{array}\right. \quad \text {for all} \quad i \in I \end{aligned}$$

(12)

and, whenever $I^\prime :=M\backslash I$ is nonempty, let

$$\begin{aligned} \nu _{i^\prime }:= \sum _{j \in I\cup \{i^\prime \}} w_j B_I^{j} B_I^{i^\prime } \det G_{I, (I \cup i^\prime )\backslash j } \quad \text {for all} \quad i^\prime \in I^\prime . \end{aligned}$$

(13)

If $\nu _i>0$ for $i \in I$ and $\nu _{i^\prime }\le 0$ for all $i^\prime \in I^\prime$, then

$$\begin{aligned} P_A(x)=x-\sum \limits _{i \in I} \frac{\nu _i}{\det G_{I,I}}u_{i}. \end{aligned}$$

(14)

Moreover, among all the elements of the set $\Delta$ of all subsets $I\subset M$ there exists at least one $I\in \Delta$ for which: (1) $\det G_{I,I}\ne 0$, (2) the coefficients $\nu _i, i \in I$ given by (12) are positive, (3) the coefficients $\nu _{i^\prime }, i^\prime \in I^{\prime }$ given by (13) are nonpositive.

To obtain the closed-form expression formula for projection of a point on intersection of three halfspaces we propose the following finite algorithm for finding $\nu _i$ as given in formula (14).

Note that Iterative Scheme 3 can be easily parallelized. For three halfspaces (i.e. $m=3$ in (11)) at most 7 subsets $I\in \mathcal {K}$ need to be checked to calculate coefficients $\nu _i, i=1,2,3$ of formula (14). Note that the above defined Iterative Scheme 3 can be useful for several algorithms, i.e. for computation of next iterate in [55].

On the other hand, when considering Iterative scheme 2 with halfspaces generated as

$$\begin{aligned} H(x_{0},x_{n})\cap C_{n}, \end{aligned}$$

where $C_{n}$ are as in Proposition 4 the number of iterations can be reduced to 4. This is the content of the following Proposition.

Let $W:=H(x_0,x_n)\cap H(x_n,x_{n+1/2}) \cap A_{3}$, where $A_3$ is given by one the following

$$\begin{aligned} \left\{ \begin{array}{l} H(x_n,x_{n+1/2}),\\ H(x_0,x_{n-1}),\\ H(x_0, \tau _n x_n + (1-\tau _n) x_{n-1}),\ \tau _n\in (0,1). \end{array}\right. \end{aligned}$$

(15)

For simplicity, in Proposition 5 we use $H(a,b)=A_{3}$.

Proposition 5

For finding projection of $x_0$ onto W with the help of Iterative Scheme 3 at most 4 subsets $I\in {\mathcal {K}}$ need to be checked.

Proof

We show that the projection of $x_0$ onto W does not require the cases $I=\{1\}, I=\{3\}, I=\{1,3\}$ to be checked.

• 1. Suppose $I=\{1\}$. Then $\nu _1=\frac{\langle x_0-x_n \ |\ x_0 - x_n \rangle }{\Vert x_0-x_n\Vert ^2}=1 , \eta _2=\langle x_{n+1/2} \ |\ x_n-x_{n+1/2} \rangle$ and for $2 \in K\backslash I$ we have

  $$\begin{aligned} \langle x_0-\nu _1 (x_0-x_n) \ |\ x_n-x_{n+1/2} \rangle -\eta _2>0. \end{aligned}$$

• 2. Suppose $I=\{3\}$. Then

  $$\begin{aligned} \nu _3=\frac{\langle x_0-b \ |\ a-b \rangle }{\Vert a-b\Vert ^2} \end{aligned}$$

  and for $1 \in K\backslash I$ we have

  $$\begin{aligned}&\langle x_0-\nu _3 (a-b) \ |\ x_0-x_n \rangle - \eta _1\nonumber \\&\quad =\langle P_{H(a,b)}(x_0)-x_n \ |\ x_0 - x_n \rangle \nonumber \\&\quad =\langle P_{H(a,b)}(x_0)-x_n \ |\ x_0 -P_{H(a,b)}(x_0) \rangle \nonumber \\&\qquad +\langle P_{H(a,b)}(x_0)-x_n \ |\ P_{H(a,b)}(x_0) - x_n \rangle \ge 0. \end{aligned}$$

  (16)

  If equality in (16) holds then $P_{H(a,b)}(x_0)=x_n$. Then for $2 \in K\backslash I$ we have

  $$\begin{aligned}&\langle x_0-\nu _3(a-b) \ |\ x_n - x_{n+1/2} \rangle - \eta _2\\&\quad =\langle P_{H(a,b)}(a,b)-x_{n+1/2} \ |\ x_n - x_{n+1/2} \rangle \\&\quad = \langle x_n-x_{n+1/2} \ |\ x_n - x_{n+1/2} \rangle >0. \end{aligned}$$

• 3. Suppose, $I=\{1,3\}$. Then

  $$\begin{aligned} \nu _3&=-\Vert x_0-x_n\Vert ^2 \langle a -b \ |\ x_0-x_n \rangle + \langle x_0-b \ |\ a-b \rangle \Vert x_0-x_n\Vert ^2\\&=\Vert x_0-x_n\Vert ^2 \langle x_n - b \ |\ a-b \rangle \le 0 \end{aligned}$$

  because $x_n\in H(a,b)$.

This shows that the choices $I=\{1\}, I=\{3\}, I=\{1,3\}$ do not lead to suitable projection weights $\nu _i\ge 0, i=1,2,3$. $\square$

4 Convergence analysis

In this section we analyse convergence properties of Iterative Scheme 2. To this aim we introduce attraction property (Proposition 7). The proposed results provide:

• new measure of quality of the solution generated by Iterative Scheme 2. Note that it was shown in [2, 19] that with every iteration, $x_n$ is further from $x_0$. However, there was no results relating $x_n$ and the solution $P_Z(x_0)$. By attraction property, the distance from $x_n$ to the solution $P_Z(x_0)$ need not be decreasing, however, $x_{n}$ remain in a ball centred at $P_Z(x_0)$ with radius which is a nonincreasing function of n (by (ii) of the Proposition 6);

• new evaluation criteria allowing to compare algorithms (we use them to compare experimentally algorithms with different choices of $C_n$) (Proposition 7).

We start with the following technical lemma.

Lemma 1

Let U be a real Hilbert space and let $u_{1},u_{2},u_{3}\in U, u_3\in H(u_1,u_2), w=\frac{1}{2}(u_1+u_3), r:=\Vert w-u_1\Vert$. Then

• (i) $\Vert w-u_2\Vert \le \frac{1}{2}\Vert u_1-u_3\Vert$,

• (ii) $\Vert u_2-u_3\Vert ^2\le b(u_2)$, where $b(\cdot ):=4r^2-\Vert \cdot -u_1\Vert ^2$.

• (iii) Moreover, if $u_4\in H$ and $u_2\in H(u_1,u_4)$, then $b(u_2)\le b(u_4)$.

Proof

• (i) We have

  $$\begin{aligned} r&= \Vert w-u_1\Vert =\Vert \frac{1}{2}u_1+\frac{1}{2}u_3-u_1\Vert =\frac{1}{2}\Vert u_3-u_1\Vert \\&= \Vert \frac{1}{2}u_1+\frac{1}{2}u_3-u_3\Vert =\Vert w-u_3\Vert . \end{aligned}$$

  By contradiction, suppose $\Vert w-u_2\Vert > \frac{1}{2}\Vert u_1-u_3\Vert$. Since $u_3\in H(u_1,u_2)$ we have

  $$\begin{aligned} \Vert u_3-u_2\Vert ^2&+\Vert u_1-u_2\Vert ^2\\&=\Vert u_3-u_2\Vert ^2+\Vert u_1-u_2\Vert ^2+2 \langle u_3-u_2 \ |\ u_2 - u_1 \rangle + 2 \langle u_3- u_2 \ |\ u_1 - u_2\rangle \\&= \Vert u_3- u_1 \Vert ^2 +2 \langle u_3- u_2 \ |\ u_1 - u_2\rangle \le \Vert u_3-u_1\Vert ^2=4r^2. \end{aligned}$$

  On the other hand

  $$\begin{aligned} 4r^2&=\Vert u_3-u_1\Vert ^2\ge \Vert u_3-u_2\Vert ^2+\Vert u_1-u_2\Vert ^2\\&=\Vert u_3-w \Vert ^2 - 2 \langle u_3-w \ |\ u_2 - w \rangle + \Vert u_2 - w \Vert ^2\\&\quad +\,\Vert u_1-w\Vert ^2 -2 \langle u_1-w \ |\ u_2 - w \rangle + \Vert u_2-w\Vert ^2\\&= 2r^2+2 \Vert u_2-w \Vert ^2 -2 \langle u_3+u_1-2w \ |\ u_2 - w \rangle > 4r^2, \end{aligned}$$

  a contradiction.

• (ii) We have

  $$\begin{aligned} \Vert u_3-u_2\Vert ^2&= \langle u_3-u_2 \ |\ u_3-u_2 \rangle = \langle u_3-u_2 \ |\ u_1 - u_1 + u_3-u_2 \rangle \\&= \langle u_3-u_2 \ |\ u_1-u_2 \rangle + \langle u_3-u_2 \ |\ u_3- u_1 \rangle \\&\le \langle u_3-u_2 \ |\ u_3- u_1 \rangle = \langle u_3-u_2-u_1+ u_1 \ |\ u_3-u_1 \rangle \\&= \langle u_3-u_1 \ |\ u_3-u_1 \rangle + \langle u_1- u_2 \ |\ u_3- u_1 \rangle \\&= 4r^2 + \langle u_1- u_2 \ |\ u_2 - u_2 + u_3- u_1 \rangle \\&= 4r^2 + \langle u_1 - u_2 \ |\ u_2-u_1 \rangle + \langle u_1-u_2 \ |\ u_3-u_2 \rangle \\&\le 4r^2 - \Vert u_1-u_2\Vert ^2. \end{aligned}$$

• (iii) The assertion (iii) stems from the fact that $u_2\in H(u_1,u_4)$ implies $\Vert u_1-u_2\Vert ^2\ge \Vert u_1-u_4\Vert ^2$ and

  $$\begin{aligned} \Vert u_3-u_2\Vert ^2\le \Vert u_1-u_3\Vert ^2 - \Vert u_1-x_{n}\Vert ^2\le \Vert u_1-u_3\Vert ^2 - \Vert u_1-u_4\Vert ^2. \end{aligned}$$

$\square$

We show that all the points $x_{n}, n\in {\mathbb {N}}$, generated by Iterative Scheme 2 are contained in the ball centred at $w:=\frac{1}{2}(x_0+{\bar{x}})$ with radius $r:=\Vert w-x_0\Vert =\frac{1}{2}\text {dist\,}(x_{0},Z)$ and the distance from $x_n$ to the solution ${\bar{x}}$ is bounded from above by a nonincreasing sequence.

Proposition 6

Let $x_0\in H\times G$. Any sequence $\{x_n\}_{n\in {\mathbb {N}}}$ generated by Iterative Scheme 2 satisfies the following:

• (i) $\Vert w-x_n\Vert \le \frac{1}{2}\Vert x_0-{\bar{x}}\Vert , n\in {\mathbb {N}}$.

• (ii) $\Vert x_n-{\bar{x}}\Vert ^2\le b_n$, where $b_n:=4r^2-\Vert x_n-x_0\Vert ^2\ge 0, n\in {\mathbb {N}}$.

• (iii) Moreover, if $x_n\in H(x_{0},x_{n-1})$ for all $n\ge 1$, the sequence $\{b_n\}_{n\in {\mathbb {N}}}$ is nonincreasing. If for some $n\ge 1$ we have $x_{n-1}\ne x_{n}$, then

  $$\begin{aligned} \begin{aligned}&\Vert {\bar{x}}-x_n\Vert ^2< \Vert x_0-{\bar{x}}\Vert ^2 - \Vert x_0-x_{n-1}\Vert ^2, \\&b_n < b_{n-1}. \end{aligned} \end{aligned}$$

  (17)

Proof

Let $n\in {\mathbb {N}}$. We have ${\bar{x}}\in H(x_0,x_n)$. We obtain (i) and (ii) by applying Lemma 1 with $u_1=x_0, u_2=x_n$ and $u_3={\bar{x}}$.

The assertion (iii) follows from (iii) of Lemma 1 with $u_1=x_0, u_2=x_n, u_3={\bar{x}}$ and $u_4=x_{n-1}$. Moreover, if for some $n\ge 1$ we have $x_{n-1}\ne x_{n}$, then $\Vert x_0-x_n\Vert ^2 > \Vert x_0-x_{n-1}\Vert ^2$, which follows from 2 of Proposition 1. $\square$

Let us note that Iterative Scheme 2 is sufficiently general to encompass algorithm 2.1 of [2] as well as any algorithm with memory introduced by $C_n$ satisfying the requirements of Proposition 2. In consequence, Proposition 6 provides properties of sequences $\{x_n\}_{n\in {\mathbb {N}}}$ constructed in these algorithms.

Corollary 1

For any $x_0\in H\times G$ and $x_n,\ x_{n+1/2}, n\ge 1$ generated by Iterative Scheme 2 we have

$$\begin{aligned} \Vert x_{n+1/2}-{\bar{x}}\Vert ^2\le \Vert x_0-{\bar{x}}\Vert ^2-\Vert x_n-x_0\Vert ^2-\Vert x_{n+1/2}-x_n\Vert ^2 \end{aligned}$$

for any ${\bar{x}}\in H(x_0,x_n)\cap H(x_n,x_{n+1/2})$.

Proof

Let $n\in {\mathbb {N}}$. Applying (ii) of Lemma 1 to $u_1=x_0, u_2=x_n, u_3={\bar{x}}$

$$\begin{aligned} \Vert x_n-{\bar{x}}\Vert ^2\le \Vert x_0-{\bar{x}}\Vert ^2-\Vert x_n-x_0\Vert ^2. \end{aligned}$$

(18)

Applying again (ii) of Lemma 1 to $u_1=x_n,\ u_2=x_{n+1/2}, u_3={\bar{x}}$ we obtain

$$\begin{aligned} \Vert x_{n+1/2}-{\bar{x}}\Vert ^2\le \Vert x_n-{\bar{x}}\Vert ^2-\Vert x_{n+1/2}-x_n\Vert ^2. \end{aligned}$$

(19)

In consequence, we have $\Vert x_{n+1/2}-{\bar{x}}\Vert \le \Vert x_n-{\bar{x}}\Vert$. Combining (18) and (19) we obtain

$$\begin{aligned} \Vert x_{n+1/2}-{\bar{x}}\Vert ^2\le & {} \Vert x_n-{\bar{x}}\Vert ^2-\Vert x_{n+1/2}-x_n\Vert ^2\\\le & {} \Vert x_0-{\bar{x}}\Vert ^2-\Vert x_n-x_0\Vert ^2 -\Vert x_{n+1/2}-x_n\Vert ^2. \end{aligned}$$

$\square$

To prove Proposition 7, which is our main result in this section we need the following Lemma.

Lemma 2

Let U be a real Hilbert space and let $D\subset U$ be a nonempty subset of U. Let $u_{1},u_{2},u_{3},u_{4}\in U$ and $u_3\in H(u_1,u_2) \cap H(u_2,u_4) \cap D, w=\frac{1}{2}(u_1+u_3), r:=\Vert w-u_1\Vert$.

Let ${\bar{q}}\in H(u_1,u_2)\cap H(u_2,u_4)\cap D$. Then ${\bar{q}} \in H(u_1,q)$, where $q=Q(u_1,u_2,u_4):=P_{H(u_1,u_2)\cap H(u_2,u_4)}(u_1)$ and

$$\begin{aligned}&\Vert u_1-{\bar{q}}\Vert ^2\ge \Vert u_1-q\Vert ^2+\Vert {\bar{q}}-q\Vert ^2,\\&\Vert u_3-{\bar{q}} \Vert ^2 \le 4r^2 - \Vert u_1-{\bar{q}}\Vert ^2 \le 4r^2- \Vert u_1-q\Vert ^2-\Vert {\bar{q}}-q\Vert ^2. \end{aligned}$$

Proof

It is immediate that ${\bar{q}}\in H(u_1,q)$. Thus

$$\begin{aligned}&\Vert u_1-{\bar{q}}\Vert ^2=\Vert u_1-q\Vert ^2 + 2\langle u_1-q \ |\ q - {\bar{q}} \rangle + \Vert {\bar{q}}-q\Vert ^2\ge \Vert u_1-q\Vert ^2+\Vert {\bar{q}}-q\Vert ^2. \end{aligned}$$

By Lemma 1, since $u_3\in H(u_1,{\bar{q}})$, we have $\Vert u_3-{\bar{q}}\Vert \le 4r^2-\Vert u_1-{\bar{q}}\Vert ^2$ which completes the proof. $\square$

To compare best approximation algorithms as defined in [2] with the Iterative Scheme 2 with memory we concentrate on single step gains. To this end let us denote $q_n:=P_{D(n)}(x_0), x_n:=P_{D(n-1,n)}(x_0)$, where $D(n)=H(x_0,x_{n-1})\cap H(x_{n-1},x_{n-1+1/2})$ as e.g. in [2] and $D(n-1,n)=H(x_0,x_{n-1})\cap H(x_{n-1},x_{n-1+1/2})\cap C_{n-1}$ with $C_{n-1}$ as in Proposition 4.

Proposition 7

(Attraction property) Sequences $\{x_n\}_{n\in {\mathbb {N}}}, \{x_{n+1/2}\}_{n\in {\mathbb {N}}}$ generated by Iterative Scheme  2 satisfy the following:

• (i) $\Vert x_0-x_{n}\Vert ^2\ge \Vert x_0-q_n\Vert ^2+\Vert x_{n}-q_n\Vert ^2$,

• (ii) $\Vert {\bar{x}}-x_{n}\Vert ^2 \le \Vert x_0-{\bar{x}}\Vert ^2-\Vert x_0 - x_n \Vert ^2 \le \Vert x_0-{\bar{x}}\Vert ^2-\Vert x_0 - q_n \Vert ^2 - \Vert x_{n}-q_n\Vert ^2$,

where $q_n:=P_{H(x_0,x_{n-1})\cap H(x_{n-1},x_{n-1+1/2})}(x_0)$ and ${\bar{x}}=P_Z(x_0)$.

Proof

The proof follows directly from Lemma 2 with $u_1=x_0, u_2=x_{n-1}, u_3={\bar{x}}, u_4=x_{n-1+1/2}, {\bar{q}}=P_{H(x_0,x_{n-1})\cap C_{n-1}}(x_0)$ and $D=C_{n-1}$. $\square$

Let us note that, in the case when $x_n=q_n$, by (ii), we have $\Vert {\bar{x}}-q_{n}\Vert ^2 \le \Vert x_0-{\bar{x}}\Vert ^2-\Vert x_0 - q_n \Vert ^2$. Hence, in the Iterative Scheme 2 we are interested in choices of $C_n$ which make the difference $x_n-q_n$ large. Note that in case of $C_{n-1}=H(x_{n-1}, x_{n-1+1/2}), \Vert x_{n}-q_n\Vert ^2=0$. For other choices of $C_{n-1}$ the worst case leads to $\Vert x_{n}-q_n\Vert ^2=0$, however, we can expect some improvement. Consequently, the proposed attraction property may serve as an evaluation criterion for comparing various versions of Iterative Scheme 2.

5 Proximal algorithms

Let H and G be real Hilbert spaces, let $f\,{:}\,H\rightarrow (-\infty ,+\infty ]$ and $g:\ G\rightarrow (-\infty ,+\infty ]$ be proper lower semicontinuous convex functions and let $L:\ H\rightarrow G$ be a bounded linear operator. Iterative Scheme 4 defined bellow is an application of Iterative Scheme 2 to optimization problem (1)–(4), i.e. we consider the pair of problems,

$$\begin{aligned} \min _{p\in H} F_P(p):=f(p)+g(Lp) \end{aligned}$$

(20)

and the dual problem to (20),

$$\begin{aligned} \min _{v^*\in G}\ F_D(v^*): = f^*(-L^*v^*)+g^*(v^*). \end{aligned}$$

(21)

If (20) has a solution ${\bar{p}}\in H$ and the regularity condition holds, e.g.

$$\begin{aligned} 0 \in \text {sqri} (\text {dom} \; g-L(\text {dom} \;f)), \end{aligned}$$

where $\text {dom}$ denotes the effective domain of a function and for any convex closed set S

$$\begin{aligned} \text {sqri}S:= \left\{ x\in S\ |\ \bigcup _{\lambda >0} \lambda (S-x)\ \text {is a closed linear subspace of}\ H \right\} , \end{aligned}$$

there exists ${\bar{v}}^*\in G$ solving (21) and

$$\begin{aligned} ({\bar{p}},{\bar{v}}^*)\in Z=\{ (p,v^*)\in H\times G\ |\ -Lv^*\in \partial f(x)\ \text {and}\ v^*\in \partial g(Lx) \}. \end{aligned}$$

(22)

Conversely, if $({\bar{p}},{\bar{v}}^*)\in Z$, then ${\bar{p}}$ solves (20) and ${\bar{v}}^*$ solves (21). The set Z defined by (22) is of the form (3), when $A=\partial f$ and $B=\partial g$.

Recall that for any $x\in H$ and any proper convex and lower semi-continuous function $f\,{:}\,H \rightarrow {\mathbb {R}}\cup \{+\infty \}$ the proximity operator $\text {Prox}_f(x)$ is defined as the unique solution to the optimization problem

$$\begin{aligned} \min _{y\in H} \left( f(y) + \frac{1}{2} \Vert x-y\Vert ^2 \right) . \end{aligned}$$

Theorem 4

[7, Example 23.3] Let $f\,{:}\,H \rightarrow {\mathbb {R}}\cup \{+\infty \}$ be a proper convex lower semi-continuous function, $x\in H$ and $\gamma >0$. Then

$$\begin{aligned} J_{\gamma \partial f}(x)=\text {Prox}_{\gamma f} (x). \end{aligned}$$

Convergence properties of Iterative Scheme 4 are summarized in Proposition 2.

5.1 Generalization to finite number of functions

Let M and K be natural numbers. Let $E=\bigoplus _{i=1}^M H_i \times \bigoplus _{k=1}^K G_k$, where $H_i, G_k$ are real Hilbert spaces, $i=1,\ldots ,M, k=1,\ldots ,K$. Let $f_i:\ H_i \rightarrow {\mathbb {R}}\cup \{+\infty \}$ and $g_k:\ G_i \rightarrow {\mathbb {R}}\cup \{+\infty \}$ be proper lower semicontinuous convex functions and $L_{ik}:\ H_i \rightarrow G_k$ be bounded linear operators, $i=1,\ldots ,M, k=1,\ldots ,K$. Consider the primal problem

$$\begin{aligned} \min _{p_1\in H_1,\ldots ,p_M \in H_M} \quad \sum _{i=1}^{M} f_i(p_i) + \sum _{k=1}^{K} g_k\left( \sum _{i=1}^{M} L_{ik}p_i\right) . \end{aligned}$$

(23)

Problem formulation (23) is general enough to cover problem arising in diverse applications including signal and image reconstruction, compressed sensing and machine learning [29]. The dual problem to (23) is

$$\begin{aligned} \min _{v_1^*\in G_1,\ldots ,v_K^* \in G_K} \quad \sum _{i=1}^{M} f_i^*\left( -\sum _{k=1}^K L_{ki}^* v_k^* \right) + \sum _{k=1}^{K} g_k^*(v_k^*). \end{aligned}$$

(24)

Assume that

$$\begin{aligned} (\forall i \in \{1,\ldots ,M\}) \quad 0 \in \text {ran} \left( \partial f_i + \sum _{k=1}^{K} L_{ki}^* \circ \partial g_k \circ L_{ik}\right) , \end{aligned}$$

where $\text {ran} D$ denotes the range of an operator D.

Then the set

$$\begin{aligned} \begin{aligned} Z&:=\bigg \{ (p_1,\ldots ,p_M,v_1^*,\ldots ,v_K^*)\in E \ |\ -\sum _{k=1}^{K} L_{ki}^* v_k^* \in \partial f_i(p_i), \\&\quad \sum _{i=1}^{M} L_{ik} p_i \in \partial g_k^* (v_k^*), i=1\ldots ,M,\ k=1,\ldots ,K \bigg \} \end{aligned} \end{aligned}$$

(25)

is nonempty and if $({\bar{p}}_1,\ldots ,{\bar{p}}_M,{\bar{v}}_1^*,\ldots ,{\bar{v}}_K^*)\in Z$ then $({\bar{p}}_1,\ldots ,{\bar{p}}_M)$ solves (23) and $({\bar{v}}_1^*,\ldots ,{\bar{v}}_K^*)$ solves (24). To find an element of set Z defined by (25) we propose the Iterative Scheme 5.

Let us note that Proposition 2 can be easily generalized to cover also the case of the set Z defined by (25).

6 Experimental results

The goal of this section is to illustrate and analyze the performance of the proposed Iterative Scheme 5 in solving problem (23), i.e. we aim at illustrating the main contribution of our work: (a) to show experimentally the influence of the choice of set $C_n$ on the convergence of the algorithm and (b) to show experimentally that the proposed attraction property provide an additional measure of the distance of the current iterate to the solution. We provide numerical results related to simple convex image inpaiting problem. The considered problem can be rewritten as an instance of (23) by setting $M=1, K=2, H = {\mathbb {R}}^{3D}$ and finding $\min _{p\in H} \quad f_1(p) + \sum _{k=1}^{2} g_k\left( L_{k}p\right)$, where functions $f_1, g_1$ and $g_2$ correspond to positivity constraint, data fidelity term and total variation (TV) based regularization [49], respectively. We focus on the analysis of influence of the choice of $C_{n}$ on the convergence. To this end we report the number of iterations of the algorithm with different $C_{n}$ settings performed to reach a tolerance $\Vert p_{n+1}-p_{n}\Vert / \left( 1 + \Vert p_{n}\Vert \right)$ less than $\epsilon$ in two successive iterations. The considered algorithms are denoted hereafter by PDBA-C0, PDBA-C1, PDBA-C2, PDBA-C3, for $C_{n}=H(x_{n},x_{n+1/2})$ and $C_{n}$ defined by (8)–(10), respectively. In the case of PDBA-C3 $\tau _n$ is set to 0.5. Numerically, the convergence rate improvement is measured by ItR defined as a ratio of the numbers of iterations consumed by PDBA-Ci (where i takes value 0, 1, 2, 3) and those consumed by PDBA-C0. The algorithms performance is illustrated by the following curves: (a) signal to noise ratio (SNR) and (b) the bounds given by Proposition 6 as a functions of iteration number.

Table 1 Reconstruction results from incomplete data with $\epsilon = 10^{-2}, \lambda _n=1, \gamma _n = 0.005, \mu _n = 0.005$

Table 2 Reconstruction results from incomplete data with $\epsilon = 10^{-2}, \lambda _n=1, \gamma _n = 0.01, \mu _n = 0.01$

Table 3 Reconstruction results from incomplete data with $\epsilon = 10^{-2}, \lambda _n=1, \gamma _n = 1.5, \mu _n = 1.5$.

The evaluation experiments concern the image inpainting problem which corresponds to the recovery of an image ${\bar{p}} \in {\mathbb {R}}^{3D}$ from lossy observations $y =L_1{\bar{p}}$, where $L_1 \in {\mathbb {R}}^{3D\times 3D}$ is a diagonal matrix such that for $i = 1, \ldots , D$ we have $L_1 (i,i) = L_1 (2i,2i)=L_1 (3i,3i)=0$, if the pixel i in the observation image y is lost and $L_1 (i,i)= L_1 (2i,2i)=L_1 (3i,3i) = 1$, otherwise. The considered optimization problem is of the form

$$\begin{aligned} \min _{p \in H} \quad \iota _{y}(L_1 p) + \iota _{{\mathcal {S}}}(p) + TV(p) \end{aligned}$$

(26)

where $\iota$ is the indicator function defined as:

$$\begin{aligned} \iota _{\mathcal {S}}(p) = {\left\{ \begin{array}{ll} 0 &{} \text {if}\quad p \in {\mathcal {S}}\\ +\infty &{} \text {otherwise},\\ \end{array}\right. } \end{aligned}$$

(27)

$TV : {\mathbb {R}}^{3D} \mapsto {\mathbb {R}}$ is a discrete isotropic total variation functional [49], i.e. for every $p \in {\mathbb {R}}^{3D}, TV(p)=g(L_2 p): =\omega \left( \sum _{d=1}^D([\Delta ^{\mathrm {h}} p]_d)^2 + ([\Delta ^{\mathrm {v}} p]_d)^2 \right) ^{1/2}$ with $L_2 \in {\mathbb {R}}^{6D\times 3D}, L_2:= \left[ (\Delta ^{\mathrm {h}})^\top \;\;(\Delta ^{\mathrm {v}})^\top \right] ^\top$, where $\Delta ^{\mathrm {h}}\in {\mathbb {R}}^{3D\times 3D}$ (resp. $\Delta ^{\mathrm {v}} \in {\mathbb {R}}^{3D\times 3D}$) corresponds to a horizontal (resp. vertical) gradient operator,

$$\begin{aligned}&[\Delta ^{\mathrm {h}} p]_d:=[(\Delta ^{\mathrm {h}} p)_{d},(\Delta ^{\mathrm {h}} p)_{2d},(\Delta ^{\mathrm {h}} p)_{3d}]\in {\mathbb {R}}^{3},\\&[\Delta ^{\mathrm {v}} p]_d:=[(\Delta ^{\mathrm {v}} p)_{d},(\Delta ^{\mathrm {v}} p)_{2d},(\Delta ^{\mathrm {v}} p)_{3d}] \in {\mathbb {R}}^{3} \end{aligned}$$

and $\omega$ denotes regularization parameter. The function $\iota _{{\mathcal {S}}}(p)$ is imposing the solution to belong to the set ${\mathcal {S}} = \left[ 0,1\right] ^{3D}$. The dual problem to (26) is the following optimization problem [14, Example 3.24, 3.26, 3.27]:

$$\begin{aligned} \begin{aligned} \min _{v_1 \in G_1,\ v_2 \in G_2}\quad&\langle y\ |\ v_1 \rangle + \sup _{r \in S} \langle r\ |\ - L_1^* v_1 - L_2^*v_2 \rangle + TV^*(v_2) \end{aligned} \end{aligned}$$

(28)

where $TV^*(v_2) = \omega \iota _{B} (\frac{v_2}{\omega })$, convex set $B=\lbrace v \in {\mathbb {R}}^{6D}: \Vert v \Vert _2 \le 1 \rbrace , G_1={\mathbb {R}}^{3D}, G_2={\mathbb {R}}^{6D}$. In the following experiments, we consider the cases of lossy observations with $\kappa$ randomly chosen pixels which are unknown.

In the following we examine the cases of $\kappa$ set to 20%, 40%, 60%, 80%, 90% (hereafter ${\tilde{\kappa }}$ denotes a fraction of missing pixels). For all the algorithms we used the initialization $x_0 = \left[ y, L_1 y, L_2 y\right] ^T$. The test were performed on image fruits from public domain (source: www.hlevkin.com/TestImages) of size $D =240 \times 256$.

Table 4 Reconstruction results from incomplete data with $\epsilon = 10^{-2}, \kappa =20\%$

Table 5 Reconstruction results from incomplete coefficients with $\epsilon = 10^{-2}, \kappa =20\%, \gamma _n = 0.005, \mu _n = 0.005$

Fig. 1

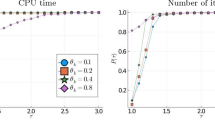
a The $240 \times 256$ clean fruits image, b the same image for which 80% randomly chosen missing pixels, and c the solution generated by Algorithm 5 PDBA-C1 after 3000 iterations, (d–e) and (f–g) show SNR and attraction property values (i.e. $-\Vert (p_0,v_0^*)-(p_n,v_{n}^*)\Vert$) versus iterations, respectively. Algorithm PDBA-C0 and PDBA-C1 are denoted in green and blue, respectively. a Original. b Degraded. c Ours result. d SNR ($\gamma _n = 0.01, \mu _n = 0.01$). e Bounds ($\gamma _n = 0.01, \mu _n = 0.01$). f SNR ($\gamma _n = 0.003, \mu _n = 0.003$). g Bounds ($\gamma _n = 0.003, \mu _n = 0.003$)

In our first experiment, we study the influence of the choice of $C_{n}$ for different settings of $\gamma _n, \mu _n$ and $\lambda _n$, which play a significant role in convergence analysis. The results summarized in Tables 1, 2 and 3, correspond to the choice of $\gamma _n=\mu _n$ equal to 0.005, 0.01 and 1.5, respectively. These results show that independently of the choice of parameters $\gamma _n, \mu _n$ algorithm PDBA-C1 leads to the best performance, while the results obtained with PDBA-C2 and PDBA-C3 are comparable to PDBA-C0. Specifically, within our setting the numbers of iterations consumed by PDBA-C1 range from 40 to 75% of those consumed by PDBA-C0, while the SNR, values of TV and inpainting residues are negligible. By inspecting Tables 1, 2 and 3, one can observe that the obtained results depend strongly upon to the choice of $\gamma _n$ and $\mu _n$.

We would like to emphasize that ideally the termination tolerance should be a function of parameters $\gamma _n, \mu _n$ and $\lambda _n$. The results presented in Table 4 shows that in the case of $\gamma _n$ and $\mu _n$ equal to 0.003 or 100 the tolerance should be smaller to prevent premature termination. In these cases the iteration number is very low, however the values of TV and SNR are significantly different than for the other choices. The premature termination is due to flat slope of the convergence curve. Similar effect can be observed when $\lambda _n = 0.8$ (see Table 5).

In the second experiment, we compare PDBA-C0 and PDBA-C1 (best over Algorithms with memory according to the first experiment). We present reconstruction results (see Table 4) as well as supplying convergence curves (see Fig. 1), i.e. SNR and bound as a function of iterations. Hereafter we call bounds as $-\Vert (p_0,v_0^*)-(p_n,v_{n}^*)\Vert ^2=-\Vert x_0-x_n\Vert ^2$ (see (ii) of Proposition 7). One can observe that PDBA-C1 leads to a faster convergence and the bounds are more tight (in the sense of Proposition 7 (ii)). The difference is the most important in the early stage of the iterations. Both algorithms slow down afterwards. For $\gamma _n=0.01$ (resp. $\mu _n = 0.01$) both versions of the algorithm lead to some numerical oscillations in convergence, which are no more visible for settings $\gamma _n=0.003$ (resp. $\mu _n = 0.003$).

7 Conclusions

In this paper we concentrate on a design of the novel scheme by incorporating memory into projection algorithm. We propose a new way of introducing memory effect into projection algorithms through incorporating into the algorithm projections onto polyhedral sets built as intersections of halfspaces constructed with the help of current and previous iterates. To this end we provide the closed-form expressions and the algorithm for finding projections onto intersections of three halfspaces. Moreover, we adapt the general scheme proposed in [50] to particular halfspaces which may arise in the course of our Iterative Scheme. This allows us to limit the number of steps for finding projections. Building upon these results, we propose a new primal–dual splitting algorithm with memory for solving convex optimization problems via general class of monotone inclusion problems involving parallel sum of maximally monotone operators composed with linear operators. To analyse convergence we prove the attraction property. The attraction property provides us with an evaluation criterion allowing to compare projection algorithms with and without memory. Our experimental results related to preliminary implementation of the algorithms have shown that the proposed algorithm with memory generally needs smaller number of iterations than the corresponding original one [2]. Although only three strategies of introducing memory effect are analysed in this work, the generality of the presented theoretical results allow us to address versatility of the approach by constructing various forms of the algorithm which use information from former steps.