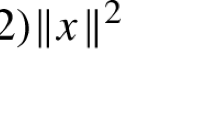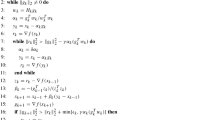Skip to main content
SpringerLink
Log in

How good are extrapolated bi-projection methods for linear feasibility problems?

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

We consider extrapolated projection methods for solving linear feasibility problems. Both successive and sequential methods of a two-set projection scheme are examined. The best algorithm in the class of algorithms that we considered was an extrapolated sequential method. When this was compared to an interior point method using the CUTEr/Netlib linear programming test problems it was found that the bi-projection method was fastest (or equal fastest) for 31% of the cases, while the interior point code was fastest in 71% of the cases. The interior-point method succeeded on all examples, but the best bi-projection method considered here failed to solve 37% of the problems within reasonable CPU time or iteration thresholds.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bauschke, H.H., Combettes, P.L., Kruk, S.G.: Extrapolation algorithm for affine-convex feasibility problems. Numer. Algorithms 41(3), 239–274 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  2. Censor, Y., Chen, W., Combettes, P.L., Davidi, R., Herman, G.T.: On the effectiveness of projection methods for convex feasibility problems with linear inequality constraints. Comput. Optim. Appl. (2011). doi:10.1007/s10589-011-9401-7

    Google Scholar 

  3. Combettes, P.L.: Hilbertian convex feasibility problem: Convergence of projection methods. Appl. Math. 35(3), 311–330 (1997)

    MathSciNet  MATH  Google Scholar 

  4. Davis, T.A., Hager, W.W.: Dual multilevel optimization. Math. Program. 112(2), 403–425 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Davis, T.A., Hager, W.W.: A sparse proximal implementation of the lp dual active set algorithm. Math. Program. 112(2), 275–301 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91(2), 201–213 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  7. Gould, N.I.M.: How good are projection methods for convex feasibility problems? Comput. Optim. Appl. 40(1), 1–12 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Gould, N.I.M., Orban, D., Toint, Ph.L.: CUTEr (and SifDec), a Constrained and Unconstrained Testing Environment, revisited. ACM Trans. Math. Softw. 29(4), 373–394 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  9. Gould, N.I.M., Orban, D., Toint, Ph.L.: GALAHAD—a library of thread-safe fortran 90 packages for large-scale nonlinear optimization. ACM Trans. Math. Softw. 29(4), 353–372 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  10. Pierra, G.: Decomposition through formalization in a product space. Math. Program. 28(1), 96–115 (1984)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computational Science and Engineering Department, Rutherford Appleton Laboratory, Chilton, Oxfordshire, OX11 0QX, England, UK

    Nicholas I. M. Gould

Authors
  1. Nicholas I. M. Gould
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nicholas I. M. Gould.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.

(TEX 4.09 KB)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gould, N.I.M. How good are extrapolated bi-projection methods for linear feasibility problems?. Comput Optim Appl 51, 1089–1095 (2012). https://doi.org/10.1007/s10589-011-9414-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-011-9414-2

Keywords

Search

Navigation