Connected domination critical graphs with respect to relative complements

Abstract

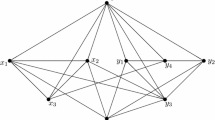
A dominating set in a graph G is a connected dominating set of G if it induces a connected subgraph of G. The minimum number of vertices in a connected dominating set of G is called the connected domination number of G, and is denoted by γ _c (G). Let G be a spanning subgraph of K _s,s and let H be the complement of G relative to K _s,s ; that is, K _s,s = G ⊕ H is a factorization of K _s,s . The graph G is k-γ _c -critical relative to K _s,s if γ _c (G) = k and γ _c (G + e) < k for each edge e ∈ E(H). First, we discuss some classes of graphs whether they are γ _c -critical relative to K _s,s . Then we study k-γ _c -critical graphs relative to K _s,s for small values of k. In particular, we characterize the 3-γ _c -critical and 4-γ _c -critical graphs.