Skip to main content
SpringerLink
Log in

A note on the independent domination number of subset graph

  • Published:
Czechoslovak Mathematical Journal Aims and scope Submit manuscript

Abstract

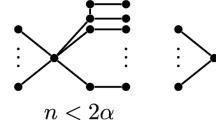
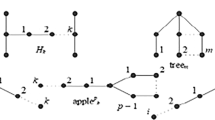
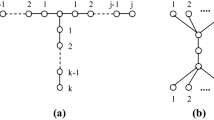
The independent domination number i(G) (independent number β(G)) is the minimum (maximum) cardinality among all maximal independent sets of G. Haviland (1995) conjectured that any connected regular graph G of order n and degree δ ≤ 1/2n satisfies i(G) ≤ ⌈2n/3δ⌉ 1/2δ. For 1 ≤ k ≤ l ≤ m, the subset graph S m (k, l) is the bipartite graph whose vertices are the k- and l-subsets of an m element ground set where two vertices are adjacent if and only if one subset is contained in the other. In this paper, we give a sharp upper bound for i(S m (k, l)) and prove that if k + l = m then Haviland’s conjecture holds for the subset graph S m (k, l). Furthermore, we give the exact value of β(S m (k, l)).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. J. Cockayne and S. T. Hedetniemi: Independence graphs. Proc. 5th Southeast Conf. Comb. Graph Theor. Comput. Utilitas Math., Boca Raton, 1974, pp. 471–491.

  2. O. Favaron: Two relations between the parameters of independence and irredundance. Discrete Math. 70 (1988), 17–20.

    Article  Google Scholar 

  3. J. Haviland: On minimum maximal independent sets of a graph. Discrete Math. 94 (1991), 95–101.

    Article  Google Scholar 

  4. J. Haviland: Independent domination in regular graphs. Discrete Math. 143 (1995), 275–280.

    Article  Google Scholar 

  5. M. A. Henning and P. J. Slater: Inequality relating domination parameters in cubic graphs. Discrete Math. 158 (1996), 87–98.

    Article  Google Scholar 

  6. E. J. Cockayne, O. Favaron, C. Payan and A. G. Thomason: Contributions to the theory of domination, independence and irredundance in graphs. Discrete Math. 33 (1981), 249–258.

    Article  Google Scholar 

  7. P. C. B. Lam, W. C. Shiu and L. Sun: On independent domination number of regular graphs. Discrete Math. 202 (1999), 135–144.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dept. of Math., Shantou University, Shantou, Guangdong, 515063, P.R. China

    Xue-gang Chen

  2. The College of Information Science and Engineering, Shandong University of Science and Technology, Taian, Shandong Province, 271019, P.R. China

    De-xiang Ma

  3. Dept. of Mathematics, Langfang Normal College, Langfang, Hebei, 065000, P.R. China

    Hua-Ming Xing

  4. Department of Applied Mathematics, Beijing Institute of Technology, Beijing, 100081, P.R. China

    Liang Sun

Authors
  1. Xue-gang Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. De-xiang Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hua-Ming Xing
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liang Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xue-gang Chen.

Additional information

This work was supported by National Natural Sciences Foundation of China (19871036).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chen, Xg., Ma, Dx., Xing, HM. et al. A note on the independent domination number of subset graph. Czech Math J 55, 511–517 (2005). https://doi.org/10.1007/s10587-005-0042-9

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10587-005-0042-9

Keywords

Search

Navigation