Skip to main content

Global and hemispheric temperatures revisited

Climatic Change volume 94, pages 333–349 (2009)Cite this article

Abstract

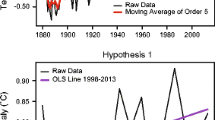
To characterize observed global and hemispheric temperatures, previous studies have proposed two types of data-generating processes, namely, random walk and trend-stationary, offering contrasting views regarding how the climate system works. Here we present an analysis of the time series properties of global and hemispheric temperatures using modern econometric techniques. Results show that: The temperature series can be better described as trend-stationary processes with a one-time permanent shock which cannot be interpreted as part of the natural variability; climate change has affected the mean of the processes but not their variability; it has manifested in two stages in global and Northern Hemisphere temperatures during the last century, while a second stage is yet possible in the Southern Hemisphere; in terms of Article 2 of the Framework Convention on Climate Change it can be argued that significant (dangerous) anthropogenic interference with the climate system has already occurred.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

References

  • Andreou A, Spanos A (2003) Statistical adequacy and the testing of trend versus difference stationary. Econom Rev 22:217–237

    Article  Google Scholar 

  • Banerjee A, Lumsdaine RL, Stock JH (1992) Recursive and sequential tests of the unit root and trend break hypotheses: theory and international evidence. JBES 10(3):271–287

    Article  Google Scholar 

  • Bloomfield P (1992) Trend in global temperature. Clim Change 21:1–16

    Article  Google Scholar 

  • Bruckner T, Schellnhuber HJ (1999) Climate change protection: the tolerable windows approach. (IPTS Report 34)

  • Crowley TJ (2000) Causes of climate change over the past 1000 years. Science 289:270–277

    Article  Google Scholar 

  • Dickey DA, Fuller WA (1979) Distribution of the estimators for autoregressive time series with a unit root. J Am Stat Assoc 74:427–431

    Article  Google Scholar 

  • Elliott G, Rothenberg TJ, Stock JH (1996) Efficient tests for an autoregressive unit root. Econometrica 64:813–836

    Article  Google Scholar 

  • Enders W (2003) Applied econometric time series. Wiley, New York

    Google Scholar 

  • Folland CK et al (1992) Observed climate variability and change. In: Houghton JT, Callander BA, Varney SK (eds) Climate change 1992: the supplementary report to the IPCC scientific assessment. Cambridge University Press, Cambridge

    Google Scholar 

  • Folland CK et al (2001a) Global temperature change and its uncertainties since 1861. Geophys Res Lett 28:2621–2624

    Article  Google Scholar 

  • Folland CK et al (2001b) Observed climate variability and change. In: Houghton JT et al (eds) Climate change 2001: the scientific basis. Cambridge Univ Press, Cambridge, pp 99–181

    Google Scholar 

  • Galbraith J, Green C (1992) Inference about trends in global temperature data. Clim Change 22:209–221

    Article  Google Scholar 

  • Gay C, Estrada F, Conde C (2007) Some implications of time series analysis for describing climatologic conditions and for forecasting. An illustrative case: Veracruz, Mexico. Atmosfera 20(2):147–170

    Google Scholar 

  • Hansen J, Lebedeff S (1987) Global trends of measured surface air temperature. J Geophys Res 92:13345–13372

    Article  Google Scholar 

  • Harvey DI, Mills TC (2000) Detecting climate change using smooth transitions. (Economic Research Paper 00/21, Department of Economics, Loughborough University); (available at http://www.lboro.ac.uk/departments/ec/Research/Discussion%20Papers%202000/Research%20Papers%202000/erp00–21.pdf)

  • Harvey DI, Mills TC (2002) Unit roots and double smooth transitions. J Appl Stat 29(5):675–683

    Article  Google Scholar 

  • Hatanaka M (1996) Time-series-based econometrics. Unit roots and cointegration. Oxford University Press, Oxford

    Google Scholar 

  • Hodrick RJ, Prescott EC (1997) Postwar U.S. business cycles: an empirical investigation. J Money Credit Bank 29:1–16

    Article  Google Scholar 

  • IPCC (2001) Climate change 2001: synthesis report 2001. In: Watson RT, the Core Writing Team (eds) Contribution of working group I, II, and III to the third assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, 397 pp

    Google Scholar 

  • IPCC (2007) Climate change 2007: the physical science basis. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, 996 pp

    Google Scholar 

  • Joachim H, Schnellnhuber HJ et al (ed) (2006) Avoiding dangerous climate change. Cambridge University Press, Cambridge

    Google Scholar 

  • Jones PD, Mann ME (2004) Climate over past millennia. Rev Geophys 42:RG2002. doi:10.1029/2003RG000143

    Article  Google Scholar 

  • Jones PD, Moberg A (2003) Hemispheric and large-scale surface air temperature variations: an extensive revision and an update to 2001. J Clim 16:206–223

    Article  Google Scholar 

  • Jones PD et al (2001) Adjusting for sampling density in grid-box land and ocean surface temperature time series. J Geophys Res 106:3371–3380

    Article  Google Scholar 

  • Kärner O (1996) Global temperature deviations as a random walk. J Climate 9:656–658

    Article  Google Scholar 

  • Kaufmann RK, Stern DI (1997) Evidence for human influence on climate from hemispheric temperature relations. Nature 388:39–44

    Article  Google Scholar 

  • Kaufmann RK, Kauppi H, Stock JH (2006a) Emissions, concentrations, & temperature: a time series analysis. Clim Change 77:249–278. doi:10.1007/s10584-006-9062-1

    Article  Google Scholar 

  • Kaufmann RK, Kauppi H, Stock JH (2006b) The relationship between radiative forcing and temperature: what do statistical analyses of the instrumental temperature record measure? Clim Change 77:279–289. doi:10.1007/s10584-006-9063-0

    Article  Google Scholar 

  • Kim D, Perron P (2007) Unit root tests allowing for a break in the trend function under both the null and the alternative hypotheses. Unpublished manuscript. Department of Economics, Boston University

  • Kwiatkowski D, Phillips PCB, Schmidt P, Shin Y (1992) Testing the null hypothesis of stationarity against the alternative of a unit root. J Econom 54:159–178

    Article  Google Scholar 

  • Lumsdaine R, Papell DH (1997) Multiple trend breaks and the unit-root hypothesis. REStat 79(2):212–218

    Google Scholar 

  • MacKinnon JG (1996) Numerical distribution functions for unit root and cointegration tests. J Appl Econ 11:601–618

    Article  Google Scholar 

  • Maddala GS, Kim IM (1998) Unit roots, cointegration and structural change. Themes in Modern Econometrics, Cambridge Univ Press

  • Mann ME, Jones PD (2003) Global surface temperature over the past two millennia. Geophys Res Lett 30(15):1820. doi:10.1029/2003GL017814

    Article  Google Scholar 

  • Mann ME, Bradley RS, Hughes MK (1998) Global scale temperature patterns and climate forcing over the past six centuries. Nature 392:779–787

    Article  Google Scholar 

  • Mann ME, Bradley RS, Hughes MK (1999) Northern Hemisphere temperatures during the past millennium: inferences, uncertainties and limitations. Geophys Res Lett 26:759–762

    Article  Google Scholar 

  • Nelson CR, Plosser CI (1982) Trends and random walks in macroeconomic time series: some evidence and implications. J Monet Econ 10:139–162

    Article  Google Scholar 

  • Ng S, Perron P (2001) Lag length selection and the construction of unit root tests with good size and power. Econometrica 69(6):1519–1554

    Article  Google Scholar 

  • Ng S, Perron P (2005) A note on the selection of time series models. OBES, Department of Economics, University of Oxford, vol 67, no 1, pp 115–134, 02

  • Perron P (1989) The great crash, the oil price shock, and the unit root hypothesis. Econometrica 99:1361–1401

    Article  Google Scholar 

  • Perron P, Vogelsang T (1993) Erratum: the great cash, the oil price shock and the unit root hypothesis. Econometrica 61:248–249

    Article  Google Scholar 

  • Perron P (1997) Further evidence on breaking trend functions in macroeconomic variables. J Econom 80(2):355–385

    Article  Google Scholar 

  • Perron P, Qu Z (2007) A simple modification to improve the finite sample properties of Ng and Perron’s unit root tests. Econ Lett 94:12–19

    Article  Google Scholar 

  • Perron P, Yabu T (2007) Testing for shifts in trend with an integrated or stationary noise component. Forthcoming in JBES. Available at http://people.bu.edu/perron/papers/breakpaper.pdf

  • Perron P, Zhu X (2005) Structural breaks with deterministic and stochastic trends. J Econom 129:65–119

    Article  Google Scholar 

  • Said E, Dickey DA (1984) Testing for unit roots in autoregressive moving average models of unknown order. Biometrika 71:599–607

    Article  Google Scholar 

  • Schneider SH (2002) Can we estimate the likelihood of climatic changes at 2100? Clim Change 52(4):441–451

    Article  Google Scholar 

  • Spanos A, Mcguirk A (2002) Where do statistical models come from? The problem of specification uncertainty in empirical modeling. (Virginia Tech working paper) (available at http://www.econ.ucy.ac.cy/seminars/Spanos.pdf)

  • Stern DI, Kaufmann RK (1997) Time series properties of global climate variables: detection and attribution of climate change. (Working Papers in Ecological Economics. The Australian National University, Center for Resource and Environmental Studies Ecological Economics Programme) (available at http://eprints.anu.edu.au/archive/00000665/00/eep9702.pdf)

  • Stern DI, Kaufmann RK (1999) Is there a global warming signal in hemispheric temperature series? (Working Papers in Ecological Economics. The Australian National University, Center for Resource and Environmental Studies Ecological Economics Programme) (available at http://www.bu.edu/cees/research/workingp/pdfs/9903.pdf)

  • Stock JH (1994) Unit roots, structural breaks, and trends. In: Engle R, McFadden D (eds) Handbook of econometrics, vol IV, pp 2739–2841. North-Holland, New York

    Google Scholar 

  • Vogelsang TJ, Perron P (1998) Additional tests for a unit root allowing the possibility of breaks in the trend function. Int Econ Rev 39:1073–1100

    Article  Google Scholar 

  • Woodward WA, Gray HL (1993) Global warming and the problem of testing for trend in time series data. J Clim 6:953–962

    Article  Google Scholar 

  • Woodward WA, Gray HL (1995) Selecting a model for detecting the presence of a trend. J Clim 8:1929–1937

    Article  Google Scholar 

  • Zheng X, Basher RE (1999) Structural time series models and trend detection in global and regional temperature series. J Clim 12:2347–2358

    Article  Google Scholar 

  • Zivot E, Andrews D (1992) Further evidence on the Great Crash, the oil price shock, and the unit root hypothesis. JBES 10(3):251–270

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centro de Ciencias de la Atmósfera, UNAM, Ciudad Universitaria, Circuito Exterior, México, DF, 04510, México

    Carlos Gay-Garcia & Francisco Estrada

  2. Instituto de Investigaciones Económicas, Universidad Nacional Autónoma de México, México, DF, 04510, México

    Armando Sánchez

Authors
  1. Carlos Gay-Garcia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Francisco Estrada
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Armando Sánchez
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Carlos Gay-Garcia.

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Gay-Garcia, C., Estrada, F. & Sánchez, A. Global and hemispheric temperatures revisited. Climatic Change 94, 333–349 (2009). https://doi.org/10.1007/s10584-008-9524-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10584-008-9524-8

Keywords

  • Unit Root
  • Unit Root Test
  • Temperature Series
  • Trend Function
  • Hemispheric Temperature