Abstract
Two semi-analytical one-degree-of-freedom secular models are presented for the motion of small bodies beyond Neptune. A special attention is given to trajectories entirely exterior to the planetary orbits. The first one is the well-known non-resonant model of Kozai (Astron J 67:591, 1962) adapted to the transneptunian region. Contrary to previous papers, the dynamics is fully characterized with respect to the fixed parameters. A maximum perihelion excursion possible of 16.4 AU is determined. The second model handles the occurrence of a mean-motion resonance with one of the planets. In that case, the one-degree-of-freedom integrable approximation is obtained by postulating the adiabatic invariance, and is much more general and accurate than previous secular models found in the literature. It brings out in a plain way the possibility of perihelion oscillations with a very high amplitude. Such a model could thus be used in future studies to deeper explore that kind of motion. For complex resonant orbits (especially of type 1 : k), a segmented secular description is necessary since the trajectories are only “integrable by parts”. The two models are applied to the Solar System but the notations are kept general so that it could be used for any quasi-circular and coplanar planetary system.

















Similar content being viewed by others
Notes
To prevent any confusion in the following, note that the present paper will never deal with the so-called “secular resonances”. What we call here a “resonant secular model” is a secular model that takes into account a mean-motion resonance between the particle and one of the planets.
The expansion of Kozai (1962) makes use of the inverse ratio: he was indeed interested of trajectories entirely interior to the orbit of Jupiter.
Even if the semi-analytical model is also valid for a perihelion inside the planetary region, we still limit the study to \(q>a_\text {N}\) as this is the region of interest in the scope of this paper. For details about the non-resonant secular dynamics with a perihelion inside the planetary region, see Thomas and Morbidelli (1996) or Gallardo et al. (2012).
Note that an analytical search for the two separatrices at \(\omega =\pi /2\) using an expansion of (17) at order 2 of G around the equilibrium does show an asymptotic flat width at about 16.4065975 AU.
We recall that the \(\{{\varLambda }_i\}\) momenta were added artificially to the Hamiltonian to absorb its temporal dependence. Given that \({\varGamma }=k_pL+k{\varLambda }_p\), it is not surprising to get an entire liberty concerning its value.
That separation prevents probably any occurrence of secondary resonance in our model.
For integrating numerically the semi-secular system, the required partial derivatives of \({\mathcal {K}}\) are obtained by inverting the derivative and integration symbols in the expression of \(\varepsilon \,{\mathcal {K}}_1\). Some nested derivatives can become a bit cumbersome: do not forget, for instance, that the true anomaly is function of e and M, themselves functions of \({\varSigma }\), U, \(\gamma \) and \(\sigma \) via (31).
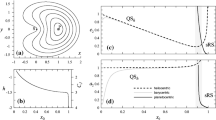
For instance, we found that the resonance 2:11 with Neptune has a double island if \(\eta _0=-0.65\), with \(\omega \sim \pi /2\) and \(\tilde{q}\sim 34\) AU (where we chose \(a_0=93.9872\) AU). However, the required range of parameters is very narrow.
The proximity of the resonance still invalidates a fully non-resonant secular model.
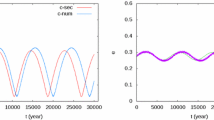
Note that such a symmetrical trajectory was improbable since at the black point the right island is much larger than the left one. A careful analysis of that orbit shows that \(\sigma \) is temporarily trapped around the saddle point and then swallowed by the growing left island. However, other integrations of the osculating and semi-secular systems show various possible behaviours, including further stay in the right island with a large area, or temporary maintenance of a grazing horseshoe-type orbit (see for instance Fig. 17 just after 1 Gyr: the double peaks in the period are separatrix approaches without crossing).
References
Batygin, K., Brown, M.E.: Evidence for a distant giant planet in the solar system. Astron. J. 151, 22 (2016)
Beaugé, C., Roig, F.: A semianalytical model for the motion of the trojan asteroids: proper elements and families. Icarus 153, 391–415 (2001)
Brasil, P.I.O., Gomes, R.S., Soares, J.S.: Dynamical formation of detached trans-Neptunian objects close to the 2:5 and 1:3 mean motion resonances with Neptune. Astron. Astrophys. 564, 44 (2014)
Brown, M.E., Trujillo, C., Rabinowitz, D.: Discovery of a candidate inner Oort cloud planetoid. Astrophys. J. 617, 645–649 (2004)
Fouchard, M., Froeschlé, C., Valsecchi, G., Rickman, H.: Long-term effects of the Galactic tide on cometary dynamics. Celest. Mech. Dyn. Astron. 95, 299–326 (2006)
Gallardo, T.: Atlas of the mean motion resonances in the solar system. Icarus 184, 29–38 (2006a)
Gallardo, T.: The occurrence of high-order resonances and Kozai mechanism in the scattered disk. Icarus 181, 205–217 (2006b)
Gallardo, T., Hugo, G., Pais, P.: Survey of Kozai dynamics beyond Neptune. Icarus 220, 392–403 (2012)
Gomes, R.S., Gallardo, T., Fernández, J.A., Brunini, A.: On the origin of the high-perihelion scattered disk: the role of the Kozai mechanism and mean motion resonances. Celest. Mech. Dyn. Astron. 91, 109–129 (2005)
Gronchi, G.F., Milani, A.: The stable Kozai state for asteroids and comets. With arbitrary semimajor axis and inclination. Astron. Astrophys. 341, 928–935 (1999)
Henrard, J.: A semi-numerical perturbation method for separable Hamiltonian systems. Celest. Mech. Dyn. Astron. 49, 43–67 (1990)
Henrard, J.: Dynamics Reported—Expositions in Dynamical Systems, vol. 2. Springer, Berlin (1993)
Kinoshita, H., Nakai, H.: General solution of the Kozai mechanism. Celest. Mech. Dyn. Astron. 98, 67–74 (2007)
Knezevic, Z., Milani, A., Farinella, P., Froeschle, C., Froeschle, C.: Secular resonances from 2 to 50 AU. Icarus 93, 316–330 (1991)
Kozai, Y.: Secular perturbations of asteroids with high inclination and eccentricity. Astron. J. 67, 591 (1962)
Kozai, Y.: Secular perturbations of resonant asteroids. Celest. Mech. 36, 47–69 (1985)
Laskar, J.: Secular evolution of the solar system over 10 million years. Astron. Astrophys. 198, 341–362 (1988)
Laskar, J.: The chaotic motion of the solar system—a numerical estimate of the size of the chaotic zones. Icarus 88, 266–291 (1990)
Lemaître, A.: Resonances: models and captures. In: Souchay, J., Dvorak, R. (eds.) Lecture Notes in Physics, vol. 790, pp. 1–62. Springer, Berlin (2010)
Lemaître, A., Morbidelli, A.: Proper elements for highly inclined asteroidal orbits. Celest. Mech. Dyn. Astron. 60, 29–56 (1994)
Lidov, M.L.: The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies. Planet. Space Sci. 9, 719–759 (1962)
Milani, A., Baccili, S.: Dynamics of Earth-crossing asteroids: the protected Toro orbits. Celest. Mech. Dyn. Astron. 71, 35–53 (1998)
Moons, M., Morbidelli, A.: Secular resonances inside mean-motion commensurabilities: the 4/1, 3/1, 5/2 and 7/3 cases. Icarus 114, 33–50 (1995)
Moons, M., Morbidelli, A., Migliorini, F.: Dynamical structure of the 2/1 commensurability with Jupiter and the origin of the resonant asteroids. Icarus 135, 458–468 (1998)
Morbidelli, A.: Asteroid secular resonant proper elements. Icarus 105, 48–66 (1993)
Morbidelli, A.: Modern celestial mechanics: aspects of solar system dynamics. Taylor & Francis, London (2002)
Morbidelli, A., Levison, H.F.: Scenario for the origin of the orbits of the trans-Neptunian objects 2000 CR\(_{105}\) and 2003 VB\(_{12}\) (Sedna). Astron. J. 128, 2564–2576 (2004)
Neishtadt, A.: On the change in the adiabatic invariant on crossing a separatrix in systems with two degrees of freedom. J. Appl. Math. Mech. 51, 586–592 (1987)
Piessens, R., de Doncker-Kapenga, E., Ueberhuber, C.W.: Quadpack. A subroutine package for automatic integration (Springer Series in Computational Mathematics) (1983)
Roig, F., Simula, A., Ferraz-Mello, S., Tsuchida, M.: The high-eccentricity asymmetric expansion of the disturbing function for non-planar resonant problems. Astron. Astrophys. 329, 339–349 (1998)
Thomas, F., Morbidelli, A.: The Kozai resonance in the outer solar system and the dynamics of long-period comets. Celest. Mech. Dyn. Astron. 64, 209–229 (1996)
Tsiganis, K., Gomes, R., Morbidelli, A., Levison, H.F.: Origin of the orbital architecture of the giant planets of the solar system. Nature 435, 459–461 (2005)
Wisdom, J.: A perturbative treatment of motion near the 3/1 commensurability. Icarus 63, 272–289 (1985)
Acknowledgments
We thank Giovanni F. Gronchi and Andrea Milani for their precious advice: sometimes, even a few words can be of great help. We thank also two anonymous referees who helped us to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Appendix: Expansion of the secular non-resonant Hamiltonian
Appendix: Expansion of the secular non-resonant Hamiltonian
We present here some hints about the construction of the secular analytical non-resonant Hamiltonian function. With the planetary model chosen (Eq. 6), the angle \(\psi _i\) is simply defined by:
where:
Then, the multiple average of \(\varepsilon {\mathcal {H}}_1\) is computed in two steps, beginning with the integration over \(\lambda _1,\lambda _2\ldots \lambda _N\). As the indirect part vanishes, we have, using the Legendre development (9):
where \(\chi \) is defined as:
One can see that the odd terms have disappeared. The average over l is less straightforward, since each polynomial 2n of (58) requires the computation of \(n+1\) integrals of the form:
where \(\alpha \), \(\beta \) and r are functions of the true anomaly \(\nu \). The general form of the result is presented in Eqs. (12) and (13), and the first terms are the following
\(n = 1\) | \(n = 2\) | \(n = 3\) |
|---|---|---|
\(\alpha _1 = 1/8\) | \(\alpha _2 = 9/1024\) | \(\alpha _3 = 25/65536\) |
\(P_1^0(x) = 1\) | \(P_2^0(x) = 2+3\,x^2\) | \(P_3^0(x) = 2\,(8+40\,x^2+15\,x^4)\) |
\(Q_1^0(x) = -1+3\,x^2\) | \(Q_2^0(x) = 3-30\,x^2+35\,x^4\) | \(Q_3^0(x) = -5+105\,x^2-315\,x^4+231\,x^6\) |
\(P_2^1(x) = 10\) | \(P_3^1(x) = 210\,(2+x^2)\) | |
\(Q_2^1(x) = -1+7\,x^2\) | \(Q_3^1(x) = 1-18\,x^2+33\,x^4 \) | |
\(P_3^2(x) = 63\) | ||
\(Q_3^2(x) = -1+11\,x^2\) |
\(n = 4\) | \( n = 5\) |
|---|---|
\( \alpha _4 = 245/33554432\) | \(\alpha _5 = 567/4294967296 \) |
\(P_4^0(x) = 5\,(16+168\,x^2+210\,x^4+35\,x^6) \) | \(P_5^0(x) = 14\,(128+2304\,x^2+6048\,x^4+3360\,x^6+315\,x^8) \) |
\(Q_4^0(x) = 35-1260\,x^2+6930\,x^4-12012\,x^6+6435\,x^8 \) | \(Q_5^0(x) = -63+3465\,x^2-30030\,x^4+90090\,x^6-109395\,x^8+46189\,x^{10} \) |
\(P_4^1(x) = 630\,(48+80\,x^2+15\,x^4)\) | \(P_5^1(x) = 9240\,(32+112\,x^2+70\,x^4+7\,x^6) \) |
\(Q_4^1(x) = -1+33\,x^2-143\,x^4+143\,x^6 \) | \( Q_5^1(x) = 7-364\,x^2+2730\,x^4-6188\,x^6+4199\,x^8 \) |
\(P_4^2(x) = 1386\,(10+3\,x^2) \) | \( P_5^2(x) = 240240\,(8+8\,x^2+x^4) \) |
\(Q_4^2(x) = 1-26\,x^2+65\,x^4\) | \( Q_5^2(x) = -1+45\,x^2-255\,x^4+323\,x^6 \) |
\(P_4^3(x) = 858\) | \( P_5^3(x) = 8580\,(14+3\,x^2) \) |
\(Q_4^3(x) = -1+15\,x^2 \) | \( Q_5^3(x) = 3-102\,x^2+323\,x^4 \) |
\(P_5^4(x) = 12155 \) | |
\(Q_5^4(x) = -1+19\,x^2 \) |
\(n = 6\) | |
|---|---|
\(\alpha _6 = 7623/549755813888 \) | |
\(P_6^0(x) = 14\,(256+7040\,x^2+31690\,x^4+36960\,x^6+11550\,x^8+693\,x^{10}) \) | |
\(Q_6^0(x) = 231-18018\,x^2+225225\,x^4-1021020\,x^6+2078505\,x^8-1939938\,x^{10}+676039\,x^{12} \) | |
\(P_6^1(x) = 60060\,(128+768\,x^2+1008\,x^4+336\,x^2+21\,x^8) \) | |
\(Q_6^1(x) = -3+225\,x^2-2550\,x^4+9690\,x^6-14535\,x^8+7429\,x^{10} \) | |
\(P_6^2(x) = 90090\,(80+168\,x^2+70\,x^4+5\,x^6) \) | |
\(Q_6^2(x) = 5-340\,x^2+3230\,x^4-9044\,x^6+7429\,x^8 \) | |
\(P_6^3(x) = 12155\,(224+160\,x^2+15\,x^4) \) | |
\(Q_6^3(x) = -5+285\,x^2-1995\,x^4+3059\,x^6 \) | |
\(P_6^4(x) = 230945\,(6+x^2) \) | |
\(Q_6^4(x) = 1-42\,x^2+161\,x^4 \) | |
\(P_6^5(x) = 29393 \) | |
\(Q_6^5(x) = -1+23\,x^2\) |
Rights and permissions
About this article
Cite this article
Saillenfest, M., Fouchard, M., Tommei, G. et al. Long-term dynamics beyond Neptune: secular models to study the regular motions. Celest Mech Dyn Astr 126, 369–403 (2016). https://doi.org/10.1007/s10569-016-9700-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-016-9700-5