Skip to main content
SpringerLink
Log in

Central configurations of four bodies with an axis of symmetry

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

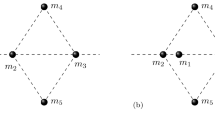
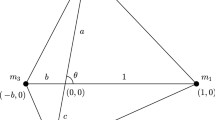
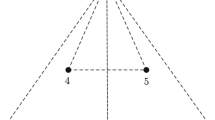
A complete solution is given for a symmetric case of the problem of the planar central configurations of four bodies, when two bodies are on an axis of symmetry, and the other two bodies have equal masses and are situated symmetrically with respect to the axis of symmetry. The positions of the bodies on the axis of symmetry are described by angle coordinates with respect to the outside bodies. The solution is such, that giving the angle coordinates, the masses for which the given configuration is a central configuration, can be computed from simple analytical expressions of the angles. The central configurations can be described as one-parameter families, and these are discussed in detail in one convex and two concave cases. The derived formulae represent exact analytical solutions of the four-body problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  • Albouy, A.: Symétrie des configurations centrales de quatre corps. C. R. Acad. Sci. Paris 320, 217–220 (1995)

    MathSciNet  Google Scholar 

  • Albouy, A.: The symmetric central configurations of four equal masses. Contemp. Math. 198, 131–136 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  • Albouy, A., Fu, Y., Sun, S.: Symmetry of planar four-body convex central configurations. Proc. R. Soc. A 464, 1355–1365 (2008)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Albouy, A., Cabral, H.E., Santos, A.A.: Some problems on the classical \(n\)-body problem. Celest. Mech. Dyn. Astron. 113, 369–375 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  • Albouy, A., Kaloshin, V.: Finiteness of central configurations of five bodies in the plane. Ann. Math. 176, 535–588 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Alvarez-Ramírez, M., Llibre, J.: The symmetric central configurations of the 4-body problem with masses \(m_1=m_2 \ne m_3=m_4\). Appl. Math. Comput. 219, 5996–6001 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  • Bernat, J., Llibre, J., Pérez-Chavela, E.: On the planar central configurations of the four-body problem with three equal masses. Math. Anal. 16, 1–13 (2009)

    MathSciNet  MATH  Google Scholar 

  • Corbera, M., Cors, J.M., Llibre, J.: On the central configurations of the planar \(1+3\) body problem. Celest. Mech. Dyn. Astron. 109, 27–43 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Cors, J.M., Roberts, G.E.: Four-body co-circular central configurations. Nonlinearity 25, 343–370 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Deng, C., Zhang, S.: Planar symmetric concave central configurations in Newtonian four-body problems. J. Geom. Phys. 83, 43–52 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Dziobek, O.: Über einen merkwürdigen Fall des Vielkörperproblems. Astron. Nach. 152, 33–46 (1900)

    Article  ADS  Google Scholar 

  • Hampton, M.: Splendid isolation: local uniqueness of the centered co-circular relative equilibria in the \(N\)-body problem. Celest. Mech. Dyn. Astr. 124, 145–153 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Hampton, M., Moeckel, R.: Finiteness of relative equilibria of the four-body problem. Invent. Math. 163, 289–312 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Leandro, E.S.G.: Finiteness and bifurcations of some symmetrical classes of central configurations. Arch. Ration. Mech. Anal. 167, 147–177 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  • Leandro, E.S.G.: On the central configurations of the planar restricted four-body problem. J. Differ. Equ. 226, 323–351 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Lehmann-Filhés, R.: Über zwei Fälle des Vielkörperproblems. Astron. Nach. 127, 137–143 (1891)

    Article  ADS  MATH  Google Scholar 

  • Long, Y., Sun, S.: Four-body central configurations with some equal masses. Arch. Ration. Mech. Anal. 162, 25–44 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  • MacMillan, W.D., Bartky, W.: Permanent configurations in the problem of four bodies. Trans. Am. Math. Soc. 34, 838–875 (1932)

    Article  MathSciNet  MATH  Google Scholar 

  • Moulton, F.R.: The straight line solutions of the problem of \(n\) bodies. Ann. Math. 12, 1–17 (1910)

    Article  MathSciNet  MATH  Google Scholar 

  • Perez-Chavela, E., Santoprete, M.: Convex four-body central configurations with some equal masses. Arch. Ration. Mech. Anal. 185, 481–494 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  • Piña, E., Lonngi, P.: Central configurations for the planar Newtonian four-body problem. Celest. Mech. Dyn. Astron. 108, 73–93 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Pizzetti, P.: Casi particolari del problema dei tre corpi. Rend. Real. Accad. Linc. 13, 17–26 (1904)

    MATH  Google Scholar 

  • Saari, D.G.: Central configurations—a problem for the twenty-first century. Exped. Math. MAA Spectrum 283–295 (2011)

  • Shi, J., Xie, Z.: Classification of four-body central configurations with three equal masses. J. Math. Anal. Appl. 363, 512–524 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  • Smale, S.: Topology and mechanics. II. The planar \(n\)-body problem. Invent. Math. 11, 45–64 (1970)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Smale, S.: Mathematical problems for the next century. Math. Intell. 20, 7–15 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  • Szenkovits, F., Ureche, V.: On homographic solutions and central configurations of the \(n\)-body problem. Rom. Astron. J. 16, 167–175 (2006)

    Google Scholar 

  • Sweatman, W.L.: Orbits near central configurations for four equal masses. Celest. Mech. Dyn. Astron. 119, 379–395 (2014)

    Article  ADS  MathSciNet  Google Scholar 

  • Wintner, A.: The analytical foundations of celestial mechanics. Princeton University Press, Princeton, NJ (1941)

    MATH  Google Scholar 

  • Xia, Z.: Convex central configurations for the \(n\)-body problem. J. Differ. Equ. 200, 185–190 (2004)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Xie, Z.: Inverse problem of central configurations and singular curve in the collinear \(4\)-body problem. Celest. Mech. Dyn. Astron. 107, 353–376 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Xie, Z.: Isosceles trapezoid central configurations of the Newtonian four-body problem. Proc. R. Soc. Edinb. A 142, 665–672 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Zhao, F., Chen, J.: Central configurations for \((pn+gn)\)-body problems. Celest. Mech. Dyn. Astron. 121, 101–106 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

We thank the referees for useful suggestions.

Author information

Authors and Affiliations

  1. Department of Astronomy, Eötvös University, Pázmány Péter sétány 1/A, Budapest, 1117, Hungary

    Bálint Érdi & Zalán Czirják

Authors
  1. Bálint Érdi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zalán Czirják
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bálint Érdi.

Appendix: The discriminant D

Appendix: The discriminant D

According to Eq. (82) and using Eqs. (78)–(80),

$$\begin{aligned} D= & {} q^2-4pr =\big [a_1(2b_0-b_1)+(b_0-a_0)(2a_0-a_1)\big ]^2(a_1+b_0-a_0)^2 \\&+\,4a_0(a_1+b_0-a_0)^2(2a_0-a_1+b_1-2b_0)(a_0b_1+a_1b_0-a_1b_1)\\= & {} (a_1+b_0-a_0)^2D_1, \end{aligned}$$

where

$$\begin{aligned} D_1= & {} \big [a_1(2b_0-b_1)+(b_0-a_0)(2a_0-a_1)\big ]^2\\&+\,4a_0(2a_0-a_1+b_1-2b_0)(a_0b_1+a_1b_0-a_1b_1) \\= & {} \big [a_1(2b_0-b_1)+b_1(2a_0-a_1)+(b_0-a_0-b_1)(2a_0-a_1)\big ]^2 \\&+\,4a_0(2a_0-a_1+b_1-2b_0)(a_0b_1+a_1b_0-a_1b_1) \\= & {} \big [2a_1b_0-a_1b_1+2a_0b_1-a_1b_1+(b_0-a_0-b_1)(2a_0-a_1)\big ]^2 \\&+\,4a_0(2a_0-a_1+b_1-2b_0)(a_0b_1+a_1b_0-a_1b_1) \\= & {} \big [2(a_0b_1+a_1b_0-a_1b_1)-(b_1+a_0-b_0)(2a_0-a_1)\big ]^2 \\&+\,4a_0(2a_0-a_1+b_1-2b_0)(a_0b_1+a_1b_0-a_1b_1) \\= & {} 4(a_0b_1+a_1b_0-a_1b_1)^2+(b_1+a_0-b_0)^2(2a_0-a_1)^2 \\&-\,4(a_0b_1+a_1b_0-a_1b_1)(b_1+a_0-b_0)(2a_0-a_1) \\&+\,4a_0(2a_0-a_1+b_1-2b_0)(a_0b_1+a_1b_0-a_1b_1) \\= & {} 4(a_0b_1+a_1b_0-a_1b_1)^2+(b_1+a_0-b_0)^2(2a_0-a_1)^2 \\&+\,4(a_0b_1+a_1b_0-a_1b_1)\big [-(b_1-b_0)(2a_0-a_1) +a_0(b_1-2b_0)\big ] \\= & {} 4(a_0b_1+a_1b_0-a_1b_1)\big [a_0b_1+a_1b_0-a_1b_1-(b_1-b_0)(2a_0-a_1) \!+\!a_0(b_1-2b_0)\big ] \\&+\,(b_1+a_0-b_0)^2(2a_0-a_1)^2 \\= & {} 4(a_0b_1+a_1b_0-a_1b_1)(a_0b_1+a_1b_0-a_1b_1-2a_0b_1+2a_0b_0+a_1b_1-a_1b_0\\&+\,a_0b_1-2a_0b_0) \\&+\,(b_1+a_0-b_0)^2(2a_0-a_1)^2=(b_1+a_0-b_0)^2(2a_0-a_1)^2. \end{aligned}$$

Thus

$$\begin{aligned} D=\big [(2a_0-a_1)(a_1+b_0-a_0)(b_1+a_0-b_0)\big ]^2. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Érdi, B., Czirják, Z. Central configurations of four bodies with an axis of symmetry. Celest Mech Dyn Astr 125, 33–70 (2016). https://doi.org/10.1007/s10569-016-9672-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10569-016-9672-5

Keywords

Search

Navigation