Abstract
If one has to attain high accuracy over long timescales during the numerical computation of the N-body problem, the method called Lie-integration is one of the most effective algorithms. In this paper, we present a set of recurrence relations with which the coefficients needed by the Lie-integration of the orbital elements related to the spatial N-body problem can be derived up to arbitrary order. Similarly to the planar case, these formulae yield identically zero series in the case of no perturbations. In addition, the derivation of the formulae has two stages, analogously to the planar problem. Namely, the formulae are obtained to the first order, and then, higher-order relations are expanded by involving directly the multilinear and fractional properties of the Lie-operator.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
When \(z_i\rightarrow 0\) and \(\dot{z}_i\rightarrow 0\) for all \(1\le i\le N\).
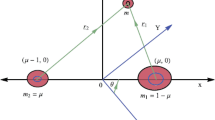
Note that the symbol M represents the central mass while the symbols \(M_i\) (with a single index) denote the mean anomalies.
References
Bancelin, D., Hestroffer, D., Thuillot, W.: Numerical integration of dynamical systems with Lie series. Relativistic acceleration and non-gravitational forces. Celest. Mech. Dyn. Astron. 112, 221–234 (2012)
Delva, M.: Integration of the elliptic restricted three-body problem with Lie series. Celest. Mech. Dyn. Astron. 34, 145–154 (1984)
Gröbner, W., Knapp, H.: Contributions to the Method of Lie-Series. Bibliographisches Institut, Mannheim (1967)
Hanslmeier, A., Dvorak, R.: Numerical integration with Lie series. Astron. Astrophys. 132, 203–207 (1984)
Pál, A., Süli, Á.: Solving linearized equations of the N-body problem using the Lie-integration method. Mon. Not. R. Astron. Soc. 381, 1515–1526 (2007)
Pál, A.: Analysis of radial velocity variations in multiple planetary systems. Mon. Not. R. Astron. Soc. 409, 975–980 (2010)
Pál, A.: Lie-series for orbital elements—I. The planar case. Celest. Mech. Dyn. Astron 119, 45–54 (2014)
Acknowledgments
The author would like to thank A. László for his helpful comments about the tensor rank analysis. The author also thanks the anonymous referees for their thorough reviews of the manuscript. The author thanks László Szabados for the careful proofreading. This work has been supported by the Hungarian Academy of Sciences via the Grant LP2012-31. Additional support is received from the Hungarian OTKA Grants K-109276 and K-104607.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Pál, A. Lie-series for orbital elements: II. The spatial case. Celest Mech Dyn Astr 124, 97–107 (2016). https://doi.org/10.1007/s10569-015-9653-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-015-9653-0