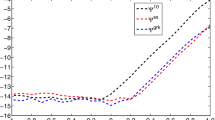
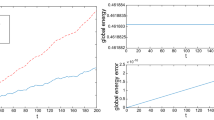
Abstract
We consider Sundman and Poincaré transformations for the long-time numerical integration of Hamiltonian systems whose evolution occurs at different time scales. The transformed systems are numerically integrated using explicit symplectic methods. The schemes we consider are explicit symplectic methods with adaptive time steps and they generalise other methods from the literature, while exhibiting a high performance. The Sundman transformation can also be used on non-Hamiltonian systems while the Poincaré transformation can be used, in some cases, with more efficient symplectic integrators. The performance of both transformations with different symplectic methods is analysed on several numerical examples.
Similar content being viewed by others
References
Blanes S., Budd C.J.: High order symplectic integrators for perturbed Hamiltonian systems. Celest. Mech. Dyn. Astron. 89, 383–405 (2004)
Blanes S., Budd C.J.: Adaptive geometric integrators for Hamiltonian problems with approximate scale invariance. SIAM J. Sci. Comput. 26, 1089–1113 (2005)
Blanes S., Moan P.C.: Practical symplectic partitioned Runge–Kutta and Runge–Kutta–Nyström methods. J. Comp. Appl. Math. 142, 313–330 (2002)
Blanes S., Casas F., Ros J.: Extrapolation of symplectic integrators. Celest. Mech. Dyn. Astron. 75, 149–161 (1999)
Blanes S., Casas F., Murua A.: Splitting and composition methods in the numerical integration of differential equations. Bol. Soc. Esp. Mat. Apl. 45, 89–145 (2008)
Bond S.D., Leimkuhler B.: Time-transformations for reversible variable step-size integration. Numer. Algor. 19, 55–71 (1998)
Budd C.J., Leimkuhler B., Piggott M.D.: Scaling invariance and adaptivity. Appl. Numer. Math. 39, 261–288 (2001)
Calvo M.P., Sanz-Serna J.M.: The development of variable-step symplectic integrators, with applications to the two-body problem. SIAM J. Sci. Comput. 14, 936–952 (1993)
Calvo M.P., Sanz-Serna J.M., López-Marcos M.A.: Variable step implementations of geometric integrators. Appl. Numer. Math. 28, 1–16 (1998)
Chan R.P.K., Murua A.: Extrapolation of symplectic methods for Hamiltonian problems. Appl. Numer. Math. 34, 189–205 (2000)
Creutz M., Gocksch A.: Higher-order hybrid Monte Carlo algorithms. Phys. Rev. Lett. 63, 9–12 (1989)
Gladman B., Duncan M., Candy J.: Symplectic integrators for long-term integrations in celestial mechanics. Celest. Mech. Dyn. Astron. 52, 221–240 (1991)
Hairer E.: Variable time step integration with symplectic methods. Appl. Numer. Math. 25, 219–227 (1997)
Hairer E., Söderlind G.: Explicit, time reversible, adaptive stepsize control. SIAM J. Sci. Comput. 26, 1838–1851 (2005)
Hairer, E., Lubich, Ch., Wanner, G.: Geometric Numerical Integration. Structure-Preserving Algorithms for Ordinary Differential Equations, vol 31, 2nd edn. Springer, Berlin (2006)
Hellström C., Mikkola S.: Explicit algorithmic regularization in the few-body problem for velocity-dependent perturbations. Celest. Mech. Dyn. Astron. 106, 143–156 (2010)
Holder T., Leimkuhler B., Reich S.: Explicit variable step-size and time-reversible integration. Appl. Numer. Math. 39, 367–377 (2001)
Huang W., Leimkuhler B.: The adaptive Verlet method. SIAM J. Sci. Comput. 18, 239–256 (1997)
Iserles A.: A First Course in the Numerical Analysis of Differential Equations. 2nd edn. Cambridge University Press, Cambridge (2008)
Kinoshita H., Yoshida H., Nakai H.: Symplectic integrators and their application to dynamical astronomy. Celest. Mech. Dyn. Astron. 50, 59–71 (1991)
Laskar J., Robutel P.: High order symplectic integrators for perturbed Hamiltonian systems. Celest. Mech. Dyn. Astron. 80, 39–62 (2001)
Leimkuhler B., Reich S.: Simulating Hamiltonian Dynamics. Cambridge University Press, Cambridge (2004)
McLachlan R.I.: Composition methods in the presence of small parameters. BIT Numer. Math. 35, 258–268 (1995a)
McLachlan R.I.: On the numerical integration of ordinary differential equations by symmetric composition methods. SIAM J. Sci. Comput. 16(1), 151–168 (1995b)
McLachlan R.I., Quispel R.G.W.: Splitting methods. Acta Numerica 11, 341–434 (2002)
McLachlan R.I., Quispel R.G.W.: Geometric integrators for ODEs. J. Phys. A Math. Gen. 39, 5251–5285 (2006)
Mikkola S.: Practical symplectic methods with time transformation for the few-body problem. Celest. Mech. Dyn. Astron. 67, 145–165 (1997)
Mikkola S., Aarseth S.: A time-transformed leapfrog scheme. Celest. Mech. Dyn. Astron. 84, 343–354 (2002)
Mikkola S., Tanikawa K.: Explicit symplectic algorithms for time-transformed Hamiltonians. Celest. Mech. Dyn. Astron. 74, 287–295 (1999)
Preto M., Tremaine S.: A class of symplectic integrators with adaptive time step for separable Hamiltonian systems. Celest. Mech. Dyn. Astron. 118, 2532–2541 (1999)
Sanz-Serna J.M., Calvo M.P.: Numerical Hamiltonian Problems. Chapman and Hall, London (1994)
Skeel R.: Variable step size destabilizes the Störmer/leapfrog/Verlet method. BIT Numer. Math. 33, 172–175 (1993)
Sophroniou M., Spaletta G.: Derivation of symmetric composition constants for symmetric integrators. Opt. Methods Softw. 20, 597–613 (2005)
Stiefel E.L., Scheifel G.: Linear and Regular Celestial Mechanics. Springer, Berlin (1971)
Suzuki M.: Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations. Phys. Lett. A 146(6), 319–323 (1990)
Wisdom J., Holman M.: Symplectic maps for the n-body problem. Astron. J. 102, 1528–1538 (1991)
Yoshida H.: Construction of higher order symplectic integrators. Phys. Lett. A 150(5–7), 262–268 (1990)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Blanes, S., Iserles, A. Explicit adaptive symplectic integrators for solving Hamiltonian systems. Celest Mech Dyn Astr 114, 297–317 (2012). https://doi.org/10.1007/s10569-012-9441-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-012-9441-z