Abstract
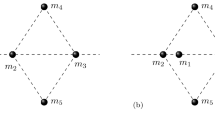
We prove that for generalized forces which are function of the mutual distance, the ring n + 1 configuration is a central configuration. Besides, we show that it is a homographic solution. We apply the above results to quasi-homogeneous potentials.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Arribas M. and Elipe A. (2004). Bifurcations and equilibria in the extended N-body ring problem. Mech. Res. Comm. 31: 1–8
Cid R., Ferrer S. and Elipe A. (1983). Regularization and linearization of the equations of motion in central force-field. Celest. Mech. 31: 73–80
Cid R. and Elipe A. (1985). On the motion of three rigid-bodies. Central configurations. Celest. Mech. 37: 113–126
Diacu, F., Pérez-Chavela, E., Santoprete, M.: The Kepler problem with anisotropic perturbations. J. Math. Phys. 46, 072701-1–21 (2005)
Elipe A. (1992). On the restricted three-body problem with generalized forces. Astrophys. Space Sci. 188: 257–269
Elipe A. and Ferrer S. (1985). On the equilibrium solution in the circular planar restricted three rigid bodies problem. Celest. Mech. 37: 59–70
Kalvouridis T.J. (1999). A planar case of the n + 1 body problem: the ring problem. Astrophys. Space Sci. 260: 309–325
Kalvouridis T.J. (2001). Zero velocity surface in the three-dimensional ring problem of N + 1 bodies. Celest. Mech. Dyn. Astron. 80: 133–144
Hadjifotinou K.G. and Kalvouridis T.J. (2005). Numerical investigation of periodic motion in the three-dimensional ring problem of N bodies. Int. J. Bifurc. Chaos 15: 2681–2688
Maxwell J.C. (1859). On the Stability of Motions of Saturn’s Rings. Macmillan and Cia., Cambridge
Mioc V. and Stavinschi M. (1998). On The Schwarzschild-type polygonal (n + 1)-body problem and on the associated restricted problem. Baltic Astron. 7: 637–651
Mioc V. and Stavinschi M. (1999). On Maxwell’s (n + 1)-body problem in the Manev-type field and on the associated restricted problem. Physica Scripta. 60: 483–490
Scheeres, D.J.: On symmetric central configurations with application to satellite motion about rings. Ph.D. Thesis. University of Michigan (1992)
Scheeres D.J. and Vinh N.X. (1991). Linear stability of a self-gravitating ring. Celest. Mech. Dyn. Astron. 51: 83–103
Wintner A. (1947). The Analytical Foundations of Celestial Mechanics. Princeton University Press, Princeton
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Arribas, M., Elipe, A., Kalvouridis, T. et al. Homographic solutions in the planar n + 1 body problem with quasi-homogeneous potentials. Celestial Mech Dyn Astr 99, 1–12 (2007). https://doi.org/10.1007/s10569-007-9083-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-007-9083-8