Skip to main content
SpringerLink
Log in

Simulation of Filtration Processes for Inhomogeneous Media and Homogenization*

  • SYSTEMS ANALYSIS
  • Published:
Cybernetics and Systems Analysis Aims and scope

Abstract

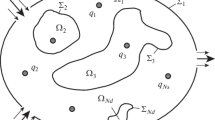
The authors analyze dynamic processes of filtration in porous media and consider periodic porous media formed by a large number of “blocks” with low permeability, separated by a connected system of “faults” with high permeability. Taking into account the structure of such media in the modeling determines the dependence of filtration equations and their coefficients on small parameters characterizing the microscale of the porous medium and permeability of the blocks. The initial–boundary-value problems for nonstationary equations of filtration in such porous media are considered and the homogenized problems that determine the approximate asymptotic solutions to such problems are given. The homogenized problems are formulated as initial–boundary-value problems for integro-differential equations with convolutions. The estimates for the accuracy of the asymptotics and relevant convergence theorems are proved. Statements about solvability and regularity have been established for the problems that are optimal and do not depend on parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. I. Lyashko, Solution of Filtration Problems by the Method of Summary Representations [in Russian], Izd. Kyiv. Univ., Kyiv (1963).

    Google Scholar 

  2. I. I. Lyashko and I. M. Velikovanenko, Numerical-Analytical Solution of Boundary-Value Problems of Filtration Theory [in Russian], Naukova Dumka, Kyiv (1973).

    Google Scholar 

  3. I. I. Lyashko, G. E. Mistetskii, and A. Ya. Oleinik, Calculation of Filtration in a Zone of Hydraulic Structures [in Russian], Budivelnyk, Kyiv (1977).

  4. A. V. Gladkiy, I. I. Lyashko, and G. E. Mistetskii, Algorithmization and Numerical Calculation of Filtration Schemes [in Russian], Naukova Dumka, Kyiv (1981).

    Google Scholar 

  5. I. I. Lyashko, L. I. Demchenko, and G. E. Mistetskii, Numerical Solution of Problems of Heat and Mass Transfer in Porous Media [in Russian], Naukova Dumka, Kyiv (1991).

    Google Scholar 

  6. S. I. Lyashko and V. V. Semenov, “Controllability of linear distributed systems in classes of generalized actions,” Cybern. Syst. Analysis, Vol. 37, No. 1, 13–32 (2001). https://doi.org/https://doi.org/10.1023/A:1016607831284.

    Article  MathSciNet  MATH  Google Scholar 

  7. A. Tymoshenko, D. Klyushin, and S. Lyashko, “Optimal control of point sources in Richards–Klute equation,” Advances in Intelligent Systems and Computing, Vol. 754, 194–203 (2019). https://doi.org/https://doi.org/10.1007/978-3-319-91008-6_20.

    Article  Google Scholar 

  8. G. V. Sandrakov, S. I. Lyashko, E. S. Bondar, and N. I. Lyashko, “Modeling and optimization of microneedle systems,” J. Autom. Inform. Sci., Vol. 51, Iss. 6, 1–11 (2019). https://doi.org/10.1615/JAutomatInfScien.v51.i6.10.

  9. G. V. Sandrakov, S. I. Lyashko, E. S. Bondar, N. I. Lyashko, and V. V. Semenov, “Modeling of configurations formed when using microneedle systems,” J. Autom. Inform. Sci., Vol. 52, Iss. 12, 1–11 (2020). https://doi.org/10.1615/JAutomatInfScien.v52.i12.10.

  10. V. V. Semenov, “Solvability of a parabolic transmission problem with the condition of a generalized proper lumped source,” Diff. Eqs., Vol. 41, No. 6, 878–886 (2005). https://doi.org/https://doi.org/10.1007/s10625-005-0227-x.

    Article  MATH  Google Scholar 

  11. V. V. Semenov, “Modified extragradient method with Bregman divergence for variational inequalities,” J. Autom. Inform. Sci., Vol. 50, Iss. 8, 26–37 (2018). https://doi.org/10.1615/JAutomatInfScien.v50.i8.30.

  12. G. V. Sandrakov, “The homogenization of nonstationary equations with contrast coefficients,” Doklady Mathematics, Vol. 56, Iss. 1, 586–589 (1997).

  13. G. V. Sandrakov, “Homogenization of parabolic equations with contrasting coefficients,” Izvestiya: Mathematics, Vol. 63, Iss. 5, 1015–1061 (1999). https://doi.org/10.1070/IM1999v063n05ABEH000264.

  14. G. V. Sandrakov, “Multiphase homogenized models for diffusion in highly nonhomogeneous media,” Doklady Mathematics, Vol. 70, Iss. 1, 507–511 (2004).

  15. G. V. Sandrakov, “Multiphase models of nonstationary diffusion arising from homogenization,” Comput. Math. and Math. Phys., Vol. 44, Iss. 10, 1741–1756 (2004).

  16. G. V. Sandrakov, “Multiphase homogenized diffusion models for problems with several parameters,” Izvestiya: Mathematics, Vol. 71, Iss. 6, 1193–1252 (2007). https://doi.org/10.1070/IM2007v071n06ABEH002387.

  17. G. Duvaut and J.-L. Lions, Les Inéquations en Mécanique et en Physique, Dunod, Paris (1972).

    MATH  Google Scholar 

  18. M. S. Agranovich and M. I. Vishik, “Elliptic problems with a parameter and parabolic problems of general type,” Russian Math. Surveys, Vol. 19, Iss. 63, 53–157 (1964). https://doi.org/10.1070/RM1964v019n03ABEH001149.

  19. N. S. Bakhvalov and G. P. Panasenko, Homogenization: Averaging Processes in Periodic Media, Kluwer, Dordrecht (1989). https://doi.org/https://doi.org/10.1007/978-94-009-2247-1.

    Article  Google Scholar 

  20. A. Bensoussan, J.-L. Lions, and G. Papanicolau, Asymptotic Analysis for Periodic Structures, North-Holland, Amsterdam (1978).

    Google Scholar 

  21. E. Sanchez-Palencia, Non Homogeneous Media and Vibration Theory, Lecture Notes in Physics, Vol. 127, Springer-Verlag, New York (1980). https://doi.org/https://doi.org/10.1007/3-540-10000-8.

  22. G. V. Sandrakov, “Homogenization of variational inequalities for obstacle problems,” Sbornik Mathematics, Vol. 196, Iss. 3–4, 541–560 (2005). https://doi.org/10.1070/SM2005v196n04ABEH000891.

  23. G. V. Sandrakov, “Homogenization of variational inequalities for non-linear diffusion problems in perforated domains,” Izvestiya: Mathematics, Vol. 69, Iss. 5, 1035–1059 (2005). https://doi.org/10.1070/IM2005v069n05ABEH002287.

  24. G. V. Sandrakov, “Homogenization of non-stationary Stokes equations with viscosity in a perforated domain,” Izvestiya: Mathematics, Vol. 61, Iss. 1, 113–141 (1997). https://doi.org/10.1070/IM1997v061n01ABEH000107.

  25. G. V. Sandrakov, “The influence of viscosity on oscillatory phenomena in linearized hydrodynamics,” Doklady Mathematics, Vol. 66, Iss. 2, 241–244 (2002).

  26. G. V. Sandrakov, “The influence of viscosity on oscillations in some linearized problems of hydrodynamics,” Izvestiya: Mathematics, Vol. 71, Iss. 1, 97–148 (2007). https://doi.org/10.1070/IM2007v071n01ABEH002352.

  27. W. Jager, R. Rannacher, and J. Warnatz (eds.), Reactive Flows, Diffusion and Transport: From Experiments via Mathematical Modeling to Numerical Simulation and Optimization, Springer-Verlag, Berlin (2007). https://doi.org/10.1007/978-3-540-28396-6.

  28. A. Mielke, S. Reichelt, and M. Thomas, “Two-scale homogenization of nonlinear reaction-diffusion systems with slow diffusion,” Netw. Heterog. Media, Vol. 9, Iss. 2, 353–382 (2014). https://doi.org/10.3934/nhm.2014.9.353.

  29. T. Sweijen, C. J. Van Duijn, and S. M. Hassanizadeh, “A model for diffusion of water into a swelling particle with a free boundary: Application to a super absorbent polymer particle,” Chemical Engineering Science, Vol. 172, 407–413 (2017). https://doi.org/https://doi.org/10.1016/j.ces.2017.06.045.

    Article  Google Scholar 

  30. W. Jager and L. Woukeng, “Homogenization of Richards’ equations in multiscale porous media with soft inclusions,” J. Diff. Eqs., Vol. 281, 503–549 (2021). https://doi.org/https://doi.org/10.1016/j.jde.2021.02.012.

    Article  MathSciNet  MATH  Google Scholar 

  31. S. Garttner, P. Frolkovic, P. Knabner, and N. Ray, “Efficiency and accuracy of micro-macro models for mineral dissolution,” Water Resources Research, Vol. 56, Iss. 8, (2020). https://doi.org/10.1029/2020WR027585.

  32. S. Garttner, P. Frolkovic, P. Knabner, and N. Ray, “Efficiency of micro-macro models for reactive two-mineral systems,” Multiscale Modeling and Simulation, Vol. 20, Iss. 1, 433–461 (2022). https://doi.org/10.1137/20M1380648.

  33. G. V. Sandrakov, “Averaging principles for equations with rapidly oscillating coefficients,” Math. USSR Sb., Vol. 68, Iss. 2, 503–553 (1991). https://doi.org/10.1070/SM1991v068n02ABEH002111.

  34. J. I. Diaz, D. Gomez-Castro, T. A. Shaposhnikova, and M. N. Zubova, “A nonlocal memory strange term arising in the critical scale homogenization of a diffusion equation with dynamic boundary conditions,” Electron. J. Diff. Eqs., Vol. 77, 1–13 (2019).

    MATH  Google Scholar 

  35. J. I. Diaz, D. Gomez-Castro, T. A. Shaposhnikova, and M. N. Zubova, “Classification of homogenized limits of diffusion problems with spatially dependent reaction over critical-size particles,” Applicable Analysis, Vol. 98, 232–255 (2019). https://doi.org/https://doi.org/10.1080/00036811.2018.1441997.

    Article  MathSciNet  MATH  Google Scholar 

  36. M. N. Zubova and T. A. Shaposhnikova, “Homogenization of a boundary-value problem in a domain perforated by cavities of arbitrary shape with a general nonlinear boundary condition on their boundaries: The case of critical values of the parameters,” J. Mathem. Sci., Vol. 244, Iss. 2, 235–253 (2020). https://doi.org/10.1007/s10958-019-04616-z.

  37. B. Benes and I. Pazanin, “Homogenization of degenerate coupled transport processes in porous media with memory terms,” Math. Methods in the Applied Sci., Vol. 42, Iss. 18, 6227–6258 (2019). https://doi.org/10.1002/mma.5718.

  38. A. Mielke and S. Reichelt, “Traveling fronts in a reaction–diffusion equation with a memory term,” J. Dynamics and Diff. Eqs. (2022). https://doi.org/https://doi.org/10.1007/s10884-022-10133-6.

    Article  Google Scholar 

  39. G. V. Sandrakov and A. L. Hulianytskyi, “Solvability of homogenized problems with convolutions for weakly porous media,” J. Numer. Appl. Math., No. 2 (134), 59–70 (2020). https://doi.org/10.17721/2706-9699.2020.2.04.

  40. G. V. Sandrakov, A. L. Hulianytskyi, and V. V. Semenov, “Modeling of filtration processes in periodic porous media,” Modeling, Control and Information Technologies, Vol. 5, 90–93 (2021). https://doi.org/10.31713/MCIT.2021.28.

  41. T. Arbogast, J. Douglas, and U. Hornung, “Derivation of the double porosity model of single phase flow via homogenization theory,” SIAM J. Math. Anal., Vol. 21, Iss. 4, 823–836 (1990). https://doi.org/10.1137/0521046.

  42. N. S. Bakhvalov and M. E. Eglit, “The limiting behaviour of periodic media with soft-modular inclusions,” Comput. Math. and Math. Phys., Vol. 35, Iss. 6, 719–729 (1995).

Download references

Author information

Authors and Affiliations

  1. Taras Shevchenko National University of Kyiv, Kyiv, Ukraine

    G. V. Sandrakov, S. I. Lyashko & V. V. Semenov

Authors
  1. G. V. Sandrakov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. I. Lyashko
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. V. Semenov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. V. Sandrakov.

Additional information

The study was financially supported by the Ministry of Education and Science of Ukraine: Project 0122U002026 and Grant of the Ministry of Education and Science of Ukraine for the prospective development of the scientific field “Mathematical Sciences and Natural Sciences” at the Taras Shevchenko National University of Kyiv.

Translated from Kibernetyka ta Systemnyi Analiz, No. 2, March–April, 2023, pp. 42–63.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sandrakov, G.V., Lyashko, S.I. & Semenov, V.V. Simulation of Filtration Processes for Inhomogeneous Media and Homogenization*. Cybern Syst Anal 59, 212–230 (2023). https://doi.org/10.1007/s10559-023-00556-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10559-023-00556-4

Keywords

Search

Navigation