Skip to main content
SpringerLink
Log in

Computer Simulation System for Nonlinear Processes Described By the Korteweg–de Vries–Burgers Equation

  • Published:
Cybernetics and Systems Analysis Aims and scope

Abstract

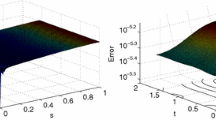
The article discusses the computer simulation system for nonlinear processes described by the Korteweg–de Vries–Burgers equation. The Korteweg–de Vries–Burgers differential equation numerically solved by the meshless approach using radial basis functions. The computer simulation system uses the following radial basis functions: Gaussian, multiquadric, inverse quadratic, inverse multiquadric, and Wu’s compactly-supported radial function. The solution of the nonlinear one-dimensional non-stationary Korteweg–de Vries–Burgers equation in the computer simulation system is visualized as a three-dimensional surface. The efficiency of the numerical solution in the computer simulation system is demonstrated by a benchmark problem for which numerical solutions were obtained, and the average relative error, average absolute error, and maximum error were calculated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. C. H. Su and C. S. Gardner, “Korteweg–de Vries equation and generalizations. III. Derivation of the Korteweg–de Vries equation and Burgers equation,” J. Math. Phys., Vol. 10, No. 3, 536–539 (1969). https://doi.org/10.1063/1.1664873.

    Article  MathSciNet  MATH  Google Scholar 

  2. R. S. Jonson, “Shallow water waves on a viscous fluid — the undular bore,” Phys. Fluids, Vol. 15, No. 10, 1693–1699 (1972). https://doi.org/10.1063/1.1693764.

    Article  MATH  Google Scholar 

  3. R. S. Jonson, “A nonlinear equation incorporating damping and dispersion,” J. Fluid Mech., Vol. 42, No. 1, 49–60 (1970). https://doi.org/10.1017/S0022112070001064.

    Article  MathSciNet  Google Scholar 

  4. H. Grad and P. N. Hu, “Unified shock profile in a plasma,” Phys. Fluids, Vol. 10, No. 12, 2596–2602 (1967). https://doi.org/10.1063/1.1762081.

    Article  Google Scholar 

  5. J. M. Burgers, “Mathematical Examples Illustrating Relations Occurring in the Theory of Turbulent Fluid Motion,” in: F. T. M. Nieuwstadt and J. A. Steketee (eds.), Selected Papers of J. M. Burgers, Springer, Dordrecht (1995), pp. 281–334. https://doi.org/10.1007/978-94-011-0195-0_10.

    Chapter  Google Scholar 

  6. J. Boussinesq, Essai sur la Théorie des Eaux Courantes, Imprimerie Nationale, Paris, (1877).

    MATH  Google Scholar 

  7. D. J. Kortewege and G. de Vries, “XLI. On the change of form of long waves advancing in a rectangular channel and on a new type of long stationary waves,” The London, Edinburgh, and Dublin Philosophical Magazine and J. of Science., Vol. 39, Iss. 240, 422–443 (1895). https://doi.org/10.1080/14786449508620739.

  8. H. Demeiray, “Nonlinear waves in a thick-walled viscoelastic tube filled with an inviscid fluid,” Int. J. Eng. Sci., Vol. 36, No. 3, 345–357 (1998). https://doi.org/10.1016/S0020-7225(97)00056-6.

    Article  MathSciNet  Google Scholar 

  9. N. Antar and H. Demiray, “Nonlinear waves in an inviscid fluid contained in a prestressed viscoelastic thin tube,” Z. Angew. Math. Phys., Vol. 48, 325–340 (1997). https://doi.org/10.1007/s000330050034.

    Article  MathSciNet  MATH  Google Scholar 

  10. S. I. Zaki, “A quintic B-spline finite elements scheme for the KdVB equation,” Comput. Meth. Appl. Mech. Eng., Vol. 188, Iss. 1–3, 121–134 (2000). https://doi.org/10.1016/S0045-7825(99)00142-5.

  11. T. S. Aly El-Danaf, “Septic B-spline method of the Kortewege–de Varies–Burger’s equation,” Commun. Nonlinear Sci. Numer. Simul., Vol. 13, Iss. 3, 554–566 (2008). https://doi.org/10.1016/j.cnsns.2006.05.010.

  12. D. Kaya, “An application of the decomposition method for the KdVB equation,” Appl. Math. Comput., Vol. 152, Iss. 1, 279–288 (2004). https://doi.org/10.1016/S0096-3003(03)00566-6.

  13. A. A. Soliman, “A numerical simulation and explicit solutions of KdV–Burgers’ and Lax’s seventh-order KdV equations,” Chaos, Solitons & Fractals, Vol. 29, Iss. 2, 294–302 (2006). https://doi.org/10.1016/j.chaos.2005.08.054.

  14. V. M. Kolodyazhny and D. O. Lisin, “Meshless method to solve nonstationary heat conduction problems using atomic radial basis functions,” Cybern. Syst. Analysis, Vol. 49, No. 3, 434–440 (2013). https://doi.org/10.1007/s10559-013-9526-z.

    Article  MathSciNet  Google Scholar 

  15. D. O. Protektor, D. A. Lisin, O. Yu. Lisina, “Numerical analysis of solutions of two-dimensional heat conduction problems by meshless approach using fundamental and general solutions,” Applied Questions of Mathematical Modelling, Vol. 2, No. 1, 98–111 (2019). 10.32782/2618-0340-2019-3-8.

  16. I. V. Garyachevskaya and D. O. Protektor, “Computer modeling system for the numerical solution of the one-dimensional non-stationary Burgers’ equation,” Bulletin of V. N. Karazin Kharkiv National University, Ser. Mathematical Modeling, Information Technology, Automated Control Systems, Vol. 43, 11–19 (2019). https://doi.org/10.26565/2304-6201-2019-43-02.

  17. H. Xie, J. Zhou, Z. Jiang, and X. Guo, “Approximations for Burgers’ equations with C-N scheme and RBF collocation methods,” J. Nonlinear Sci. Appl., Vol. 9, Iss. 6, 3727–3734 (2016). https://doi.org/10.22436/jnsa.009.06.23.

  18. E. J. Kansa, “Multiquadrics — A scattered data approximation scheme with applications to computational fluid-dynamics — I. Surface approximations and partial derivative estimates,” Comput. Math. Appl., Vol. 19, No. 8–9, 127–145 (1990). https://doi.org/10.1016/0898-1221(90)90270-T.

    Article  MathSciNet  MATH  Google Scholar 

  19. Y. C. Hon and X. Z. Mao, “An efficient numerical scheme for Burgers’ equation,” Appl. Math. Comput., Vol. 95, Iss. 1, 37–50 (1998). https://doi.org/10.1016/S0096-3003(97)10060-1.

    Article  MathSciNet  MATH  Google Scholar 

  20. Z. Wu, “Compactly supported positive definite radial functions,” Adv. Comput. Math., Vol. 4, 283–292 (1995). https://doi.org/10.1007/BF03177517.

    Article  MathSciNet  MATH  Google Scholar 

  21. C. Montoya, “Inverse source problems for the Korteweg–de Vries–Burgers equation with mixed boundary conditions,” J. Inverse Ill-Posed Probl., Vol. 27, No. 6, 777–794 (2019). https://doi.org/10.1515/jiip-2018-0108.

  22. H. P. Langtangen and S. Linge, Finite Difference Computing with PDEs, Springer, Cham (2017). https://doi.org/10.1007/978-3-319-55456-3.

  23. I. V. Sergienko, A. N. Khimich, and M. F. Yakovlev, “Methods for obtaining reliable solutions to systems of linear algebraic equations,” Cybern. Syst. Analysis, Vol. 47, No. 1, 62–73 (2011). https://doi.org/10.1007/s10559-011-9290-x.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. V. N. Karazin Kharkiv National University, Kharkiv, Ukraine

    I. V. Hariachevska & D. O. Protektor

Authors
  1. I. V. Hariachevska
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. O. Protektor
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. V. Hariachevska.

Additional information

Translated from Kibernetyka ta Systemnyi Analiz, No. 6, November–December, 2021, pp. 172–182.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hariachevska, I.V., Protektor, D.O. Computer Simulation System for Nonlinear Processes Described By the Korteweg–de Vries–Burgers Equation. Cybern Syst Anal 57, 998–1007 (2021). https://doi.org/10.1007/s10559-021-00425-y

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10559-021-00425-y

Keywords

Search

Navigation