Skip to main content
SpringerLink
Log in

A Model of Infectious Disease Spread with Hidden Carriers*

  • NEW MEANS OF CYBERNETICS, INFORMATICS, COMPUTER ENGINEERING, AND SYSTEMS ANALYSIS
  • Published:
Cybernetics and Systems Analysis Aims and scope

Abstract

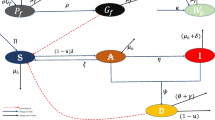
The authors consider an algorithm for estimating the unknown parameters of the infection spread model based on the Markov field tools using the maximum likelihood method. It is assumed that each state of the Markov chain represents some configuration of a finite random Markov field, and the probability distribution of the chain states is the same as general probability distribution of the states of elements of the Gibbs random field.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. T. Liggett, Interacting Particle Systems, Springer-Verlag, New York (1989).

    MATH  Google Scholar 

  2. R. K. Chornei, H. Daduna, and P. S. Knopov, “Controlled Markov fields with finite state space on graphs,” Stochastic Models, Vol. 21, Iss. 4, 847–874 (2005).

    Article  MathSciNet  Google Scholar 

  3. G. Daduna, P. S. Knopov, and R. K. Chornei, “Local control of Markovian processes of interaction on a graph with a compact set of states,” Cybern. Syst. Analysis, Vol. 37, No. 3, 348–360 (2001). https://doi.org/https://doi.org/10.1023/A:1011985609994.

  4. J. E. Besag, “Spatial interaction and the statistical analysis of lattice systems,” J. Royal Stat. Soc., Ser. B (Methodological), Vol. 36, No. 2, 192–236 (1974).

    MathSciNet  MATH  Google Scholar 

  5. A. S. Samosonok, “Asymptotic properties of maximum likelihood estimator for Gibbs fields,” Komp. Matematika, No. 1, 142–149 (2012).

    Google Scholar 

  6. A. N. Golodnikov, P. S. Knopov, and V. A. Pepelyaev, “Estimation of reliability parameters under incomplete primary information,” Theor. Decis., Vol. 57, No. 4, 331–344 (2004).

    Article  MathSciNet  Google Scholar 

  7. O. S. Samosonok “Analysis of empirical estimates obtained for Gibbs distribution parameters by the maximum likelihood method,” Cybern. Syst. Analysis, Vol. 49, No. 2, 316–324 (2013). https://doi.org/https://doi.org/10.1007/s10559-013-9514-3.

  8. P. S. Knopov and E. J. Kasitskaya, “On large deviations of empirical estimates in a stochastic programming problem with time-dependent observations,” Cybern. Syst. Analysis, Vol. 46, No. 5, 724–728 (2010). https://doi.org/https://doi.org/10.1007/s10559-010-9253-7.

  9. Yu. M. Ermoliev and P. S. Knopov, “Method of empirical means in stochastic programming problems,” Cybern. Syst. Analysis, Vol. 42, No. 6, 773–785 (2006). https://doi.org/https://doi.org/10.1007/s10559-006-0118-z.

  10. S. Geman and D. Geman, “Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images,” IEEE Trans. Pattern Anal. Mach. Intell., Vol. PAMI-6, No. 6, 721–741 (1984).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. V. M. Glushkov Institute of Cybernetics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    P. S. Knopov, O. S. Samosonok & G. D. Bilà

Authors
  1. P. S. Knopov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. S. Samosonok
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. G. D. Bilà
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. S. Knopov.

Additional information

The research was carried out with a partial support of the National Research Foundation of Ukraine (grant No. 2020.02/0121).

Translated from Kibernetyka ta Systemnyi Analiz, No. 4, July–August, 2021, pp. 166–176.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Knopov, P.S., Samosonok, O.S. & Bilà, G.D. A Model of Infectious Disease Spread with Hidden Carriers*. Cybern Syst Anal 57, 647–655 (2021). https://doi.org/10.1007/s10559-021-00390-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10559-021-00390-6

Keywords

Search

Navigation