Abstract
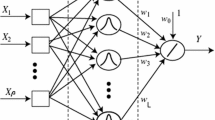
An approach to the development of a neurocontroller for controlling nonlinear dynamical objects on the basis of radial-basis function neural networks is considered. Piecewise-linear approximation of Gaussian basis functions is proposed to simplify the solution of the problem being considered. Simulation results show that the method allows one to reduce the time of construction of an object model and calculation of its control signal.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. Omatu, M. Khalid, and R. Yusof, Neural Control and Its Applications [Russian translation], IPRZhR, Moscow (2000).
K. S. Narendra and K. Parthasarathy, “Identification and control of dynamical systems using neural networks,” IEEE Trans. on Neural Networks, 1, No. 1, 4–26 (1990).
J. Moody and C. Darken, “Fast learning in networks of locally-tuned processing units,” Neural Comput., 1, 281–294 (1989).
J. T. Spooner and K. M. Passino, “Decentralized adaptive control of nonlinear systems using radial-basis neural networks,” IEEE Trans. on Automat. Contr., 44, No. 11, 2050–2057 (1999).
D. L. Yu and D. W. Yu, “A new structure adaptation algorithm for RBF networks and its application,” Neural Comput. & Appl., 16, 91–100 (2007).
R. J. Shilling, J. J. Carroll, and A. F. Al-Ajlouni, “Approximation of nonlinear systems with radial-basis function neural networks,” IEEE Trans. on Neural Networks, 12, No. 6, 1–15 (2001).
M. J. D. Powell, “Radial-basis functions for multivariable interpolation: A review,” J. C. Mason and M. G. Cox (eds.), in: Algorithm for Approximation, Oxford Un-ty Press, Oxford (1985), pp. 143–167.
G.-B. Huang, P. Saratchandran, and N. Sundarajan, “An efficient sequential learning algorithm for growing and pruning RBF (GAP-RBF) networks,” IEEE Trans. on Systems, Man, and Cybernetics, 34, No. 6, 2284–2292 (2004).
O. G. Rudenko and A. A. Bessonov, “Real-time identification of nonlinear time-varying systems using radial-basis function networks,” Cybernetics and Systems Analysis, 39, No. 6, 927–936 (2003).
A. Webb and S. Shannon, “Shape-adaptive radial based functions,” IEEE Trans. on Neural Networks, 9, No. 6, 1155–1166 (1998).
O. G. Rudenko and A. A. Bessonov, “Adaptive control of multidimensional nonlinear objects on the basis of radial-basis networks,” Cybernetics and Systems Analysis, 41, No. 2, 302–308 (2005).
S. Haykin, Neural Networks: A Comprehensive Foundation [Russian translation], Izd. Dom “Williams,” Moscow (2006).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Translated from Kibernetika i Sistemnyi Analiz, No. 1, pp. 3–13, January–February 2011.
Rights and permissions
About this article
Cite this article
Rudenko, O.G., Bezsonov, A.A., Liashenko, A.S. et al. Approximation of Gaussian basis functions in the problem of adaptive control of nonlinear objects. Cybern Syst Anal 47, 1–10 (2011). https://doi.org/10.1007/s10559-011-9285-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10559-011-9285-7