Skip to main content
SpringerLink
Log in

Nonsmooth penalty and subgradient algorithms to solve the problem of projection onto a polytope

  • Published:
Cybernetics and Systems Analysis Aims and scope

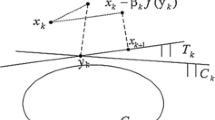
The least distance problem is considered for a convex hull of a finite family of vectors in a finite-dimensional Euclidian space. It is reduced to an equivalent nonsmooth optimization problem with a directly estimated penalty parameter for which subgradient algorithms with space dilation are proposed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. A. Nurminski, “Projection onto polyhedra in outer representation,” J. Comp. Mat. Math. Phys., 48, Issue 3, 367–375 (2008).

    Google Scholar 

  2. H. Bauschke and J. M. Borwein, “On projection algorithms for solving convex feasibility problems,” SIAM Rev., 38, No. 3, 367–426 (1996).

    Article  MATH  MathSciNet  Google Scholar 

  3. Y. Censor, M. Jiang, and A. K. Louis (eds.), “Mathematical methods in biomedical imaging and intensity-modulated radiation therapy (IMRT),” in: Publications of the Scuola Normale Superiore Subseries, CRM Series, 7 (2008).

  4. V. V. Vasin, “Fejer iterative processes in ill-posed problems with a priori information,” Izv. Vuzov, Matematika, Issue 2, 3–24 (2009).

    MathSciNet  Google Scholar 

  5. N. Z. Shor, Minimization Methods for Nondifferentiable Functions and Their Applications [in Russian], Naukova Dumka, Kyiv (1979).

    Google Scholar 

  6. P. E. Gill, W. Murray, and M. H. Wright, Practical Optimization, Academic Press, New York (1981).

    MATH  Google Scholar 

  7. B. N. Pshenichnyi, Linearization Method [in Russian], Nauka, Moscow (1983).

    Google Scholar 

  8. A. M. Priyatel’, “Solving convex programming problems by the r-algorithm with projection,” in: Analysis of the Methods of Solution of Extremum Problems: A Collection of Scientific Papers [in Russian], V. M. Glushkov Inst. of Cybernetics AS USSR (1986), pp. 24–30.

  9. A. V. Kuntsevich, “On the efficiency of applying optimization algorithms with space dilation,” Kibernetika, No. 2, 116–117 (1989).

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. V. M. Glushkov Institute of Cybernetics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    P. I. Stetsyuk

  2. Institute for Automation and Control Processes, Far Eastern Branch of Russian Academy of Sciences, Vladivostok, Russia

    E. A. Nurminski

Authors
  1. P. I. Stetsyuk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. A. Nurminski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. I. Stetsyuk.

Additional information

The study was financially supported by the joint Ukrainian-Russian project DFFD–F28.1/005 and RFFI–09–01–90413–Ukr_f_a “Subgradient methods of accelerated convergence in convex programming problems.”

Translated from Kibernetika i Sistemnyi Analiz, No. 1, pp. 59–63, January–February 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Stetsyuk, P.I., Nurminski, E.A. Nonsmooth penalty and subgradient algorithms to solve the problem of projection onto a polytope. Cybern Syst Anal 46, 51–55 (2010). https://doi.org/10.1007/s10559-010-9182-5

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10559-010-9182-5

Keywords

Search

Navigation