Skip to main content
SpringerLink
Log in

Flow Mechanism and Transient Pressure Analysis of Multi-Stage Fractured Horizontal Well

  • INNOVATIVE TECHNOLOGIES OF OIL AND GAS
  • Published:
Chemistry and Technology of Fuels and Oils Aims and scope

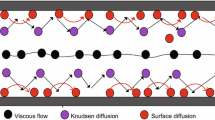
Shale gas reservoirs are typical unconventional natural gas resources characterized by low porosity and low permeability of the formation. To enhance production and provide an economically justified production rate, the multi-stage fractured horizontal well (MFHW) technology has been widely used in shale gas reservoirs. More attention has been paid recently to studying the mechanism of multi-scale flow in shale. However, the mechanism of gas seepage in shale in a multi-stage fractured horizontal well has not been systematically discussed. In the previously published conventional studies, the authors have not presented a comprehensive analysis of the adsorption, desorption, and diffusion mechanisms participating in gas seepage, particularly within a linear flow model. In this paper, the linear superposition method is applied to describe the non-Darcy flow behavior in nano/micro-scale pores and the Darcy flow behavior in macropores and natural/induced fractures in a shale matrix. Based on the flow mode, the shale reservoir and the area around the multi-stage fractured horizontal well are divided into three zones: the outer region flow, the inner region flow, and the flow in the hydraulic fractures. Based on the trilinear flow model, the authors consider the differences in properties between the initial shale reservoir and the induced fracture network of the stimulated reservoir volume (SRV). In this model, the dimensionless variables, Duhamel principle, and numerical Stehfest algorithm are combined to analyze the dynamic bottomhole pressure, adsorption-desorption behavior, multi-scale flow mechanism, and complex SRV geometry in the MFHW area. Based on the established model, the effect of the key factors and their influence on the dimensionless pressure and pressure derivate curves are considered..

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.

Similar content being viewed by others

References

  1. S. Wang et al., “Shale gas exploration: Status, problems, and prospect,” Nat. Gas Ind. B., 5(1), 60-74 (2018).

    Article  Google Scholar 

  2. C. D. Jenkins and C. M. Boyer, “Coalbed and shale gas reservoirs,” J. Pet. Technol., 60(2), 92-99 (2008).

    Article  Google Scholar 

  3. H. Sun, J. Yao, S. H. Gao, et al., “Numerical study of CO2 enhanced natural gas recovery and sequestration in shale gas reservoirs,” Int. J. Greenhouse Gas Control, 19, 406-419 (2013).

    Article  CAS  Google Scholar 

  4. A. Ghanizadeh et al., “Petrophysical and geomechanical characteristics of Canadian tight oil and liquid-rich gas reservoirs,” Fuel, 153, 664-691 (2016).

    Article  Google Scholar 

  5. D. Liu et al., “Evaluation of the role of water-shale-gas reactions on CO2 enhanced gas recovery,” Energy Proc., 154, 42-47 (2018).

    Article  CAS  Google Scholar 

  6. G. Chalmers and R. M. Bustin, “Lower Cretaceous gas shales in northeastern British Columbia, part II: evaluation of regional potential gas resources,” Bull. Can. Pet. Geol., 56(1), 22-61 (2008).

    Article  Google Scholar 

  7. D. J. K. Ross and R. M. Bustin, “Impact of mass balance calculations on adsorption capacities in microporous shale gas reservoirs,” Fuel, 86(17-18), 2696-2706 (2007).

    Article  CAS  Google Scholar 

  8. L. Chen et al., “Mechanisms of shale gas adsorption: evidence from thermodynamics and kinetics study on methane adsorption on shale,” Chem. Eng. J., 361, 559-570 (2019).

    Article  CAS  Google Scholar 

  9. P. D. Schettler, C. R. Parmely, and W. J. Lee, “Gas storage and transport in Devonian Shales,” SPE Form. Eval., 4(3), 371-376 (1986).

    Article  Google Scholar 

  10. G. R. King, “Material-balance techniques for coal seam and Devonian Shale gas reservoirs,” SPE Res. Eng., 8(01), 61-67 (1993).

    Google Scholar 

  11. F. Javadpour, “Nanopores and apparent permeability of gas flow in mudrocks,” J. Can. Pet. Technol., 48(8), 16-21 (2009).

    Article  Google Scholar 

  12. F. Civan, C. S. Rai, and C. Sondergeld, “Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms,” Transp. Porous Med., 86, 925-944 (2011).

    Article  Google Scholar 

  13. C. Guo et al., “Study on gas permeability in nanopores of shale gas reservoirs,” SPE 167179, SPE Unconventional Resources Conference, Calgary, Alberta, Canada (2013).

  14. J. F. W. Gale, E. M. Reed, and J. Holder, “Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatment,” AAPG Bull., 91(4), 603-622 (2007).

    Article  Google Scholar 

  15. E. Fathi and Y. Akkutlu, “Matrix heterogeneity effects on gas transport and adsorption in coalbed and shale gas reservoirs,” Transp. Porous Med., 80(2), 281-304 (2009).

    Article  CAS  Google Scholar 

  16. J. Guo, L. Zhang, H. Wang, et al., “Pressure transient analysis for multi-stage fractured horizontal wells in shale gas reservoirs,” Transp. Porous Med., 93(3), 635-653 (2012).

    Article  CAS  Google Scholar 

  17. S. Du, N. Yoshida, B. Liang, et al., “Application of multi-segment well approach: dynamic modeling of hydraulic fractures,” Nat. Gas Sci. Eng., 34, 886-897 (2016).

    Article  Google Scholar 

  18. X. Hu et al., “A multiscale model for methane transport mechanisms in shale gas reservoirs,” J. Pet. Sci. Eng., 172, 40- 49 (2019).

    Article  CAS  Google Scholar 

  19. E. Ozkan and M. Brown, “Comparison of fractured horizontal-well performance in conventional and unconventional reservoirs,” SPE Western Regional Meeting, San Jose, California, USA (2009).

    Book  Google Scholar 

  20. R. O. Bello and R. A. Wattenbarger, “Modeling and analysis of shale gas production with a skin effect,” J. Can. Pet. Technol., 49(12), 37-48 (2010).

    Article  Google Scholar 

  21. R. O. Bello and R. A. Wattenbarger, “Multistage hydraulically fractured shale gas rate transient analysis,” SPE North Africa Technical Conference, Cairo, Egypt (2010).

    Google Scholar 

  22. H. A. Al-Ahmadi and R. A. Wattenbarger, “Application of linear flow analysis to shale gas wells-field cases,” SPE Unconventional Gas Conference, Pittsburgh, Pennsylvania, USA (2010).

    Book  Google Scholar 

  23. E. Stalgorova and M. Louis, “Practical analytical model to simulate production of horizontal wells with branch fractures,” SPE Canadian Unconventional Resources Conference, Calgary, Canada (2012).

    Book  Google Scholar 

  24. S. Ottiger, R. Pini, G. Storti, et al., “Measuring and modeling the competitive adsorption of CO2, CH4, and N2 on a dry coal,” Langmuir, 24(17), 9531-9540 (2008).

    Article  CAS  Google Scholar 

  25. S. Mohammad, J. Fitzgerald, R. L. Robinson RL, and K. A. M. Gasem, “Experimental uncertainties in volumetric methods for measuring equilibrium adsorption,” Energy Fuels, 23(5), 2810-2820 (2009).

    Article  CAS  Google Scholar 

  26. J. C. Xu, C. H. Guo, M. Z. Wei, et al., “Production performance analysis for composite shale gas reservoir considering multiple transport mechanisms,” J. Nat. Gas Sci. Eng., 26, 382-395 (2015).

    Article  Google Scholar 

Download references

NOMENCLATURE

a — desorption coefficient;

b — pseudo-permeability coefficient, dimensionless;

C — molarity of shale gas, kmol/m3;

C — compressibility, MPa–1;

C D — dimensionless wellbore storage coefficient;

D — diffusion coefficient, m2/h;

d — diameter of pore, m;

F CD dimensionless diffusivity of fracture;

F s — shape factor of the matrix, 1/m2;

h — thickness of shale gas reservoir, m;

k — permeability, mD;

Kn — Knudsen number, dimensionless;

M — molecular weight of shale gas, kg/kmol

m — pseudo-pressure;

n — gas molar quantity, kmol;

R o — maturity of organic matter, %;

p — gas pressure, Pa;

\( \overline{p} \) — mean pressure, Pa;

pi — original reservoir pressure, Pa;

pL — Langmuir pressure, Pa;

pD — dimensionless wellbore pressure under constant production rate;

p D ′ — dimensionless wellbore pressure derivative under constant production rate;

p w — wellbore pressure, Pa;

q — production rate, m3/s;

R — gas constant, 8.314·103 Pa×m3/(kmol×K);

R CD — dimensionless fracture conductivity;

s — variable in Laplace-transform domain;

S c — skin factor;

T — temperature, K;

t — time, h;

V — adsorption of gas, m3/kg;

V E — volume concentration of shale gas in the interface of matrix and fracture, m3/m3;

V L — Langmuir volume, m3/kg;

v c — diffusion velocity of gas, m/h;

v p — permeability velocity of gas, m/h;

w F — half-width of the hydraulic fracture, m;

x e — half-length of the reservoir in the x-direction, m;

x F — half-length of the hydraulic fracture, m;

y e — half-space of the hydraulic fracture, m;

Z — compressibility of gas, dimensionless;

x, y, z — cartesian coordinates;

r — cylindrical coordinates.

Greek symbols

η — diffusivity, m2/s;

λ — mean free path of gas in pores, m;

λ — flow capacity ratio, mD/m2;

μ — viscosity of gas, cPs;

ρ — density of shale gas, kg/m3;

ρv — mass velocity, kg/(m2×s);

ρ sc — density of shale gas under standard conditions, kg/m3;

f — porosity, %;

ω — storativity ratio, dimensionless.

Subscripts

D — dimensionless variables;

O — outer zone;

I — inner zone;

F — hydraulic fracture;

f — natural fracture;

i — original variables;

i, j — subscript;

m — matrix system;

sc — standard conditions.

Author information

Authors and Affiliations

  1. The State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, China

    Ziwei Wang, Liehui Zhang & Ruihan Zhang

  2. CNPC Beijing Richfit Information Technology Co., Ltd., Beijing, China

    Ruihe Wang

  3. Research Institute of Tsinghua University in Shenzhen, Shenzhen, China

    Rui Huang

Authors
  1. Ziwei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liehui Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ruihan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ruihe Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Rui Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ziwei Wang.

Additional information

Translated from Khimiya i Tekhnologiya Topliv i Masel, No. 6, pp. 62–69, September-October, 2021.

Dimensionless variables

Dimensionless variables

Dimensionless pseudo-pressure:

$$ {m}_{\xi D}=\frac{\pi {k}_{If}h{T}_{sc}}{q_{sc}{p}_{sc}T}\left({m}_i{m}_{\xi}\right)\ \left(\xi =I, IF\right). $$
(A.1)

Dimensionless time:

$$ {t}_D=\frac{k_{If}}{{\left({\upphi}_f\upmu {c}_{tf}\right)}_i{x}_F^2}{t}_a. $$
(A.2)

Dimensionless distance (coordinates):

$$ {x}_D=\frac{x}{x_F},{x}_{eD}=\frac{x_e}{x_F},{w}_{FD}=\frac{w_F}{x_F},{y}_D=\frac{y}{x_F},{y}_{eD}=\frac{y_e}{x_F}. $$
(A.3)

Dimensionless diffusivities:

$$ {\displaystyle \begin{array}{c}{\upeta}_{\xi }=\frac{k_{\xi }}{{\left(\upphi \upmu {c}_t\right)}_{\xi i}},\xi =I,F,\\ {}{\upeta}_{FD}={\upeta}_F/{\upeta}_I.\end{array}} $$
(A.4)

Dimensionless fracture conductivity:

$$ {F}_{CD}=\frac{k_f{x}_F}{k_F{x}_F}. $$
(A.5)

The Stehfest method

$$ {m}_{wD}\left({t}_D\right)=\frac{\ln 2}{t_D}\sum_{i=1}^nV{\overline{m}}_{wD}\left({s}_i\right), $$
(B.1)
$$ {s}_i=\frac{\ln 2}{t_D}i, $$
(including)
$$ {V}_i={\left(-1\right)}^{\frac{N}{2}+i}\sum_{K=\frac{i+1}{2}}^{\min \left\{i,\frac{N}{2}\right\}}\frac{K^{\frac{N}{2}+1}(2K)!}{\left(\frac{N}{2}-K\right)!K!\left(K-1\right)!\left(i-k\right)!\left(2K-i\right)!},\mathrm{generally}\ \mathrm{N}=8. $$
(B.2)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Z., Zhang, L., Zhang, R. et al. Flow Mechanism and Transient Pressure Analysis of Multi-Stage Fractured Horizontal Well. Chem Technol Fuels Oils 57, 941–954 (2022). https://doi.org/10.1007/s10553-022-01332-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10553-022-01332-4

Keywords

Search

Navigation