Stable Stratification Effects on Flow and Pollutant Dispersion in Boundary Layers Entering a Generic Urban Environment

Abstract

Large-eddy simulations (LES) are used to investigate the effect of stable stratification on rural-to-urban roughness transitions. Smooth-wall turbulent boundary layers are subjected to a generic urban roughness consisting of cubes in an in-line arrangement. Two line sources of pollutant are added to investigate the effect on pollutant dispersion. Firstly, the LES method is validated with data from wind-tunnel experiments on fully-developed flow over cubical roughness. Good agreement is found for the vertical profiles of the mean streamwise velocity component and mean Reynolds stress. Subsequently, roughness transition simulations are done for both neutral and stable conditions. Results are compared with fully-developed simulations with conventional double-periodic boundary conditions. In stable conditions, at the end of the domain the streamwise velocity component has not yet reached the fully-developed state even though the surface forces are nearly constant. Moreover, the internal boundary layer is shallower than in the neutral case. Furthermore, an investigation of the turbulence kinetic energy budget shows that the buoyancy destruction term is reduced in the internal boundary layer, above which it is equal to the undisturbed (smooth wall) value. In addition, in stable conditions pollutants emitted above the urban canopy enter the canopy farther downstream due to decreased vertical mixing. Pollutants emitted below the top of the urban canopy are 85 % higher in concentration in stable conditions mostly due to decreased advection. If this is taken into account concentrations remain 17 % greater in stable conditions due to less rapid internal boundary-layer growth. Finally, it is concluded that in the first seven streets the vertical advective pollutant flux is significant, in contrast to the fully-developed case.

1 Introduction

In view of the global trend of urbanization there is an increasing demand for accurate predictions of urban air quality. Therefore, predicting the dispersion behaviour of pollutants within the urban canopy is of great interest. The modelling and simulation of the urban boundary layer is usually achieved by assuming that the turbulent boundary layer has fully developed over a large urban area with uniform properties (e.g. Coceal et al. 2006; Michioka et al. 2014; Boppana et al. 2014). However, in reality the overall character of the surface roughness changes from rural to suburban to urban regions, implying that the boundary layer has to adapt to the changing surface roughness. There are several studies that investigate such a roughness transition (Garratt 1990). In the past these were mostly based on analytical derivations (e.g. Townsend 1966; Macdonald 2000), but also simplified numerical models were derived (e.g. Belcher et al. 2003). Only a few numerical studies are reported that simulate flow for an explicitly resolved roughness transition (Lee et al. 2011; Cheng and Porté-Agel 2015).

Moreover, often the urban boundary layer is considered only for near-neutral conditions by assuming that the turbulence due to the presence of the obstacle results in a well-mixed flow with nearly uniform temperature. In the boundary layer pollutant concentrations increase significantly with increasing stability because the spreading downwind of the emission source is reduced due to lower turbulence levels. In urban environments the stable boundary layer occurs less often than does the unstable boundary layer (Wood et al. 2010). However, because of potentially decreased air quality in stable conditions it is important to determine when the ‘neutral urban boundary-layer assumption’ is valid. Tomas et al. (2015b) show that the turbulence added by the presence of a single two-dimensional obstacle is not enough to diminish buoyancy effects. Whether the transition of stable flow over a rural environment to a generic urban roughness consisting of multiple cubes does result in near-neutral flow is the subject of the present study. The objective is to answer the following questions:

• 1. How do stably stratified turbulent boundary layers respond to a rural-to-urban roughness transition?

• 2. Are stratification effects diminished by the added turbulence due to the roughness?

• 3. How do the roughness transition and stable stratification affect pollutant dispersion?

Use is made of large-eddy simulation (LES) to investigate a smooth-wall turbulent boundary layer exposed to a roughness transition consisting of an array of cubes in an in-line arrangement. Line sources of pollutant emission are located at two different vertical positions in front of the array. The case is studied for both neutral and stable conditions. The Reynolds number, $Re_\tau = u_\tau h / \nu$, based on the friction velocity $u_\tau$ and the obstacle height h, was between 195 at the inlet and 353 (455 in stable conditions) at the end of the domain. This is in the fully-rough regime (Snyder and Castro 2002) and in addition, Cheng and Castro (2002) showed that for flow over a similar array of sharp-edged obstacles the Reynolds number dependency is small.

In Sect. 2 the governing equations, numerical method and the considered cases are described. In Sect. 3 results for a fully-developed urban boundary-layer test case are compared with experimental data to validate the LES model. Section 4 treats the results for flow entering a generic urban canopy, focussing on the velocity fields, turbulence kinetic energy budget and concentration fields. Finally, in Sect. 5 conclusions are given.

2 Set-up of Large-eddy Simulations

2.1 Governing Equations and Numerical Method

The filtered Navier–Stokes equations in the Boussinesq approximation are

$$\begin{aligned} \frac{\partial \widetilde{u}_i}{\partial x_i}=&\,0, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \widetilde{u}_i}{\partial t} =&-\frac{\partial }{\partial x_j}\left( \widetilde{u}_i\widetilde{u}_j\right) -\frac{\partial }{\partial x_i}\left( \widetilde{p}/\rho _0+\tau _{kk}/3\right) +\frac{g}{\theta _0}\widetilde{\theta }\delta _{i3} + \nu \frac{\partial ^2\widetilde{u}_i}{\partial x_j^2} +\frac{\partial }{\partial x_j}\left( 2\nu _{sgs}S_{ij}\right) , \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial \widetilde{\varphi }}{\partial t} =&-\frac{\partial }{\partial x_j}\left( \widetilde{\varphi }\widetilde{u}_j\right) + \frac{\nu }{Pr}\frac{\partial ^2\widetilde{\varphi }}{\partial x_j^2} +\frac{\partial }{\partial x_j}\left( \frac{\nu _{sgs}}{Pr_{sgs}}\frac{\partial \widetilde{\varphi }}{\partial x_j}\right) + \mathcal {S}, \end{aligned}$$

(3)

where $\widetilde{(..)}$ denotes filtered quantities, $\widetilde{p}/\rho _0+\tau _{kk}/3$ is the modified pressure, $\tau _{kk}$ is the trace of the subgrid-scale (SGS) stress tensor, g is the acceleration due to gravity, $\nu$ is the fluid kinematic viscosity, $\nu _{sgs}$ is the SGS viscosity, Pr is the Prandtl number, $Pr_{sgs}$ is the SGS Prandtl number, $S_{ij}=\frac{1}{2}\left( \frac{\partial \widetilde{u}_i}{\partial x_j} + \frac{\partial \widetilde{u}_j}{\partial x_i}\right)$ is the rate of strain tensor and $\mathcal {S}$ is a source term. The eddy-viscosity SGS model, $\tau _{ij}= \widetilde{u_iu_j} - \widetilde{u}_i\widetilde{u}_j=-2\nu _{sgs}S_{ij}$, where $\tau$ is the SGS stress tensor, is already incorporated in Eqs. 2 and 3. Equation 3 describes the transport equation for all scalar quantities $\varphi$, which are the temperature $\theta$ and pollutant concentration $c^*$. Hereafter the $\widetilde{(..)}$ symbol is omitted for clarity; the $\overline{(..)}$ symbol represents temporal averaging.

The code developed for this study is based on the Dutch Atmospheric Large-Eddy Simulation (DALES) code (Heus et al. 2010), where the main modifications are the addition of an immersed boundary method (Pourquie et al. 2009), the implementation of inflow/outflow boundary conditions and the application of the eddy-viscosity SGS model of Vreman (2004). This model has the advantage over the standard Smagorinsky–Lilly model (Smagorinsky 1963; Lilly 1962) that no wall-damping is required to reduce the SGS energy near walls. The equations of motion are solved using second-order central differencing for the spatial derivatives and an explicit third-order Runge–Kutta method for time integration. For the scalar concentration field the second-order central $\kappa$ scheme is used to ensure monotonicity. The simulations are wall resolved; so no use is made of wall functions; Pr was 0.71 and $Pr_{sgs}$ was set to 0.9, equal to the turbulent Prandtl number found in the major part of the turbulent boundary layer in direct numerical simulation (DNS) studies by Jonker et al. (2013). The SGS Schmidt number was set to 0.9 as well. The code has been used previously to simulate turbulent flow over a surface-mounted fence, showing excellent agreement with experimental data (Tomas et al. 2015a, b).

2.2 Cases Studied

Here a summary is given of the simulation cases. Four types of simulations were performed:

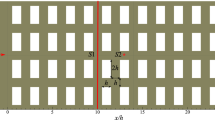
Roughness transition (RT) simulations In these simulations the roughness transition was simulated by considering a smooth-wall turbulent boundary layer of depth $\delta =10h$ that approaches an array of cubes with dimensions $h\times h \times h$ in an in-line arrangement equally spaced with a pitch of 2h, as is shown in Fig. 1. Emissions from two line sources of pollutant were simulated; one located at $z/h = 3$ and one located at $z/h = 0.2$. Both sources are located at 2h in front of the first row of cubes. The case was simulated for neutral as well as stable conditions.

Driver (D) simulations These simulations generate the smooth wall inflow turbulent boundary layers of 10h depth for the RT simulations. Inflow and outflow conditions were used in the streamwise direction. The instantaneous inlet values were generated by a recycling method described in the next section. Both neutral and stable conditions were considered and the friction Reynolds number, $Re_\tau = u_\tau h /\nu$, was 195.

Fig. 1

Domain for the RT simulations. The red rectangle represent the area over which the results for each row of cubes are averaged

Fig. 2

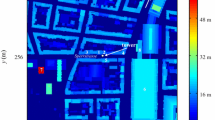
Experiment of Castro et al. (2006) with measurement locations P0–P3. The white area represents the V simulation domain. The dashed rectangle shows the repeating element

Periodic roughness (PR) simulations These simulations used the classical approach of applying periodic boundary conditions in the horizontal directions to simulate fully-developed flow. The same roughness geometry as in the RT simulations was considered on a smaller domain.

Validation (V) simulation This simulation is compared with the experimental results of Castro et al. (2006) considering fully-developed flow over an array of cubes. Figure 2 shows the geometry of the experiment. It is similar to the RT and PR simulations except that the cube arrangement is staggered. As in the PR simulation periodic boundary conditions were used in the horizontal directions. The friction Reynolds number was 371.

2.3 Domain Size and Grid

Table 1 summarizes the domain size and number of grid points used in each type of simulation. The boundary layers were generated using a horizontal domain size of $L_x \times L_y = 20\delta \times 1.8\delta$, which is sufficiently large; in Tomas et al. (2015b) it was shown that a smaller horizontal domain size of $L_x \times L_y =10\delta \times 1.57\delta$ was adequate to capture the largest flow structures in the boundary layer. The PR and V simulations used a smaller domain size than the RT simulations; decreasing the domain width did not result in differences in mean statistics.

Table 1 Domain dimensions and grid sizes

For all simulations the grid is stretched in the vertical direction. The minimal vertical grid resolution in the V simulation was 0.05h at the top of the cubes and the grid expansion ratio never exceeded 1.07. All other simulations used a minimal vertical grid spacing of 0.01h at the top of the obstacles and the expansion ratio did not exceed 1.06 inside the boundary layer. In the horizontal directions a uniform grid is used except for the inflow region of the RT simulations, where the grid is stretched with an expansion ratio of 1.02 to match the grid of the D simulation. For the PR and RT simulations the number of grid points covering each cube was $n_x \times n_y \times n_z = 20 \times 20 \times 48$; for the V simulation this was $n_x \times n_y \times n_z = 16 \times 20 \times 28$. Similar LES studies on cubical roughness reported good agreement with experimental data using lower resolutions; e.g. Kanda et al. (2004) used 10 cells in each cube dimension and Cheng and Porté-Agel (2015) used $n_x \times n_y \times n_z = 10 \times 10 \times 15$, which indicates that the grid used in the current study is adequate.

2.4 Boundary Conditions

For all cases periodicity in the spanwise direction was assumed for all variables. On the ground and obstacle walls no-slip conditions were applied, while at the top boundary a free-slip condition for the horizontal velocity components was used. For the scalars $\theta$ and $c^*$ zero-flux boundaries were assumed, except for $\theta$ at the ground and the top of the obstacles, for which isothermal conditions ($\theta =\theta _0$) were applied. In this way the total area on which $\theta =\theta _0$ is imposed is equal to the smooth-wall case, such that the average temperature boundary conditions in the canopy are similar to those for the approaching smooth-wall turbulent boundary layer. In addition, building rooftops experience a radiative cooling similar to the ground, but larger than the building side-walls. This suggests use of the same boundary conditions for the top of the cubes as are used for the ground surface.

2.4.1 Driver (D) and Roughness Transition (RT) Simulations

The inflow velocity and temperature fields were generated in separate D simulations; the instantaneous velocity field and temperature field at the inlet plane was saved in time and subsequently used as inflow data for the RT simulations. To ensure statistically steady boundary-layer characteristics the D simulations used the recycling method proposed by Lund et al. (1998) for the velocity and a similar method for the temperature (Kong et al. 2000). The only differences are that the buoyancy force was taken into account in the simulations and a mass-flux correction was applied such that the resulting inflow satisfied a constant mass flux. This procedure has been applied successfully before when considering a smooth-wall turbulent boundary layer approaching a single fence (Tomas et al. 2015b). At the outlet a convective outflow boundary condition was applied for all variables. At the top boundary a constant outflow velocity of $w=U_\infty \ \overline{d\delta _1/dx}$ was used, where $\overline{d\delta _1/dx}$ is the mean streamwise growth of the displacement thickness. This was done to establish a zero pressure gradient in the D simulations. The RT simulations used the same outflow velocity as in the D simulations.

2.4.2 Periodic Roughness (PR) and Validation (V) Simulations

At the top boundary zero vertical velocity was imposed. Periodicity was assumed in both horizontal directions and the flow was driven by a constant streamwise pressure gradient, $\partial {\varPi }/\partial x = u_\tau ^2/L_z$, with ${\varPi }=\widetilde{p}/\rho _0+\tau _{kk}/3$. Analogously, in order to achieve a statistically steady state for the temperature field in the stable PR simulation a constant volumetric temperature source, $\mathcal {S}_\theta$, was applied in all cells to balance the loss of heat at the bottom of the domain,

$$\begin{aligned} \mathcal {S}_\theta = \frac{\nu }{Pr\, L_z}\left( \frac{\partial \overline{\theta }}{\partial z}\right) _0, \end{aligned}$$

(4)

where $(\partial \overline{\theta }/\partial z)_0$ is the mean temperature gradient at the ground. A similar approach is used in Boppana et al. (2014). One may question the appropriateness of such a volumetric heat source term, but it is a remedy to an inherent characteristic of the periodic boundary conditions that are, strictly speaking, not entirely valid in the first place. Alternatively, one could prescribe a balancing heat flux at the top of the domain, but such an approach is less suitable in this case, because it tends to create a thermal boundary layer at the top wall.

2.5 Statistics

A constant timestep of 0.01T was used in the neutral simulations and 0.02T in the stable simulations. In all simulations statistics were computed after a steady state was reached; for the PR simulations this was after $10\times 10^{3}$ time scales, $T=h/U_\infty$. The D simulations required $20\times 10^{3}T$, starting from a coarse mesh simulation, while the RT simulations started from a steady-state solution generated with a steady mean inflow profile. They ran for a duration of 1300T of which the last 800T were used for computing statistics using an interval of 0.2T. The total averaging interval of 800T resulted in statistically steady results. Coceal et al. (2006) describe the statistical convergence in terms of the eddy turnover time of the largest eddies shed by the obstacles, $T_\mathrm{e}=h/u_\tau$. They find a remaining circulation in the outer region when an averaging interval of $50T_\mathrm{e}$ is used, which no longer exists when the interval is increased to $400T_\mathrm{e}$. The averaging interval used for the RT simulations corresponds to about $56T_\mathrm{e}$. However, there was no remaining circulation found in the mean flow field, most likely due to the inflow-outflow set-up in contrast to the double-periodic boundary conditions used in Coceal et al. (2006). Nevertheless, because the current results were averaged in the spanwise direction any remaining circulation is averaged out.

Fig. 3

Mean streamwise velocity component at stations P0 and P2 (a) and P1 and P3 (b). Experimental data from Castro et al. (2006)

Fig. 4

Mean Reynolds stress at stations P1(a) and P2(b). Experimental data from Castro et al. (2006)

3 LES Validation

The V simulation was performed to validate the model with data from wind-tunnel experiments (Castro et al. 2006). The experiments governed the flow over a staggered cube array for neutrally buoyant conditions. The geometry of the experiments is shown in Fig. 2. Measurements were done by means of hot-wire anemometry (HWA) outside the urban canopy and laser Doppler anemometry (LDA) within the urban canopy. The experimental set-up was similar to Cheng and Castro (2002), in which more information is given on the experimental techniques. They obtained vertical profiles of velocity statistics at four locations (P0–3); the friction Reynolds number was 937, but similar results were found in Cheng and Castro (2002) at $Re_\tau =371$, which is the friction Reynolds number used in the V simulation.

Figure 3 shows the vertical profile of the mean streamwise velocity component at four locations indicated in the figure. The agreement is quite satisfactory. However, the simulation overpredicts the length of the wake of the upstream cube, which causes the streamwise velocity component to be smaller than the experimental results at location P3.

Figure 4 shows the mean resolved Reynolds stress, $\overline{u'w'}$, at locations P1 and P2. Unfortunately, experimental data are not available at location P3. The agreement between the model and experimental results is good, although the vertical resolution was too low to resolve the peak caused by the shear layer emanating from the top of the cube. This most likely also affected the aforementioned wake length. The vertical cell size at the top of the cubes was 0.05h. In the RT and PR simulations this was decreased to 0.01h in order to capture the shear layer at the canopy height. In addition, the streamwise resolution was increased from 16 to 20 cells per cube.

For neutral stratification the mean wind profile is described by the logarthmic law,

$$\begin{aligned} \overline{u} = \frac{u_\tau }{\kappa }\text {ln}\left( \frac{z-d}{z_0}\right) , \end{aligned}$$

(5)

where $\kappa$ is the von Kármán constant (=0.4), $z_0$ is the aerodynamic roughness length and d is the displacement height, the height at which the total drag force acts (Jackson 1981). It is computed by dividing the total moment of the drag forces by the total drag force. For the V simulation d was found to be 0.63h, and by means of Eq. 5 $z_0$ was estimated to be 0.06h. Using the same method of estimating these parameters Cheng and Castro (2002) report $d=0.61h$ and $z_0=0.075h$ for their experimental results. However, they also address the difficulty in determining these parameters due to the dependency on the applied method.

4 Results of LES of Flow Entering a Generic Urban Canopy

To investigate the effect of stable stratification on flow and dispersion for a rural-to-urban roughness transition two RT simulations were done; one for neutral conditions and one for stable conditions. Two corresponding D simulations were performed to generate the turbulent inflow. In addition, two (neutral and stable) PR simulations were done using conventional periodic boundary conditions in the horizontal directions. For the neutral (stable) case a value of $4.127\times 10^{-4}$ ($7.650\times 10^{-5}$) was found for the constant streamwise pressure gradient, $\left( h/U_\infty ^2\right) \partial {\varPi }/\partial x$, in order that the velocity at the top of the domain was $U_\infty$. For the stable case a value of $7.560\times 10^{-5}$ was found for the constant volumetric temperature source, $h \mathcal {S}_\theta / \left( \left[ \theta _\infty -\theta _0\right] U_\infty \right)$, in order that the temperature at the top of the domain was $\theta _\infty$.

The applied level of stratification in the stable cases is described by the bulk Richardson number

$$\begin{aligned} Ri=\frac{\left( g/\theta _0\right) \left( \theta _\infty -\theta _0\right) \delta }{U^2_\infty }, \end{aligned}$$

(6)

which was 0.147 at the inlet of the stable D, RT and PR simulations. Local effects of stratification are described by the gradient Richardson number

$$\begin{aligned} Ri_\mathrm{grad} = \frac{g}{\theta _0}\frac{\partial \overline{\theta }}{\partial z}\Bigg / \left( 2\overline{S}_{ij}\overline{S}_{ij}\right) , \end{aligned}$$

(7)

which was 0.2 throughout most of the boundary layer in the D simulation. Increasing the stratification even more resulted in intermittent turbulence.

4.1 Instantaneous Velocity Fields

Figure 5 shows the contours of instantaneous velocity magnitude normalized with $U_\infty$ for the neutral (top) and the stable case (bottom). At the inlet the flow is already turbulent (generated in the D simulations). Low speed streaks are visible in the horizontal plane at $z=0.1h$. In the midplane both the neutral and the stable case show small-scale turbulence generated by the roughness elements. However, in the stable case the exchange of momentum in the outer region is reduced as can be seen by the more layered velocity contours.

Fig. 5

Instantaneous velocity magnitude contours for RT simulations; a neutral conditions. b stable conditions. The velocity magnitude is normalized with $U_\infty$. Plane A’ is a projection of midplane A. The $x-y$ plane is located at $z/h=0.1$ and cuts through the cubes

4.2 Mean Velocity Fields

The mean flow is statistically homogeneous in the (periodic) spanwise direction only, because the flow is developing in the streamwise direction. Assuming the mean streamwise development occurs at a larger scale than a single pitch of 2h (i.e. a ‘street’) the mean flow can be averaged over each street area, as is shown in Fig. 1. This averaging operation is indicated by $\langle ..\rangle$. Figure 6 shows the spatially-averaged mean forces for both the neutral case and the stable case. The results of the PR simulations are also shown. The friction velocity $u_\tau$ (Fig. 6a) is computed from the total drag that consists of skin frictional drag, $F_\tau$ and form drag, $F_p$. These drag forces are averaged over the area of each street,

$$\begin{aligned} F_\tau= & {} \frac{1}{2h L_y}\int _{A_{t}} \overline{\tau }\, dA, \end{aligned}$$

(8)

$$\begin{aligned} F_p= & {} \frac{1}{2h L_y}\int _{A_f} {\varDelta }\overline{p}\, dA, \end{aligned}$$

(9)

Fig. 6

Mean street-averaged forces. a Friction velocity $u_\tau$, b Skin friction coeffient $C_f$, c Form drag coefficient $C_p$, d Displacement height d. The dashed line corresponds to the PR simulation results

where $\overline{\tau } = \rho _0\nu \left( \partial \overline{u}/\partial n\right) _0$ is the mean wall shear stress, $A_t$ is the total area of all surfaces in each street (i.e. the top and side faces of the cubes as well as the ground surface), ${\varDelta }\overline{p}$ is the mean pressure difference between upwind and downwind faces of the cubes and $A_f$ is the frontal area of the cubes in each street. When $u_\tau$ reaches a constant value this is an indication of fully-developed flow at the obstacle height. For both the neutral and the stable cases this occurs after approximately seven streets ($=14h$). At the inlet $u_\tau$ is $0.0377U_\infty$ for the neutral case and $0.0172U_\infty$ for the stable case. In the canopy the neutral case converges to a friction velocity 1.84 times larger than at the inlet. The stable flow experiences a higher drag increase by the canopy because at the end of the domain $u_\tau / U_\infty$ is 2.35 times the inlet value. The skin friction coefficient, $C_f=F_\tau /\left( \frac{1}{2}\rho U_\infty ^2\right)$ and the form drag coefficient, $C_p=F_p /\left( \frac{1}{2}\rho U_\infty ^2\right)$ are shown as well (Fig. 6b, c, respectively). In the developed region form drag constitutes 76 % (81 %) of the total drag in the neutral (stable) case. This is 70 % (76 %) in the PR simulations. Finally, Fig. 6d shows the displacement height d (as defined in Sect. 3) for the four cases. Although the force coefficients seem to converge to the values found in the corresponding PR simulation, the displacement height for the RT simulation in stable conditions is significantly lower than found in the PR simulation; at the end of the domain d is 0.68h (RT) instead of 0.74h (PR). This result suggests that in stable conditions the flow at the end of the RT domain differs from the fully-developed case (PR simulation).

To investigate the streamwise development of the boundary layer Fig. 7 shows the vertical profiles of $\langle \overline{u}\rangle$ at streets 1, 4, 8, 12, 16, 20 and 24 for both neutral conditions (Fig. 7a) and stable conditions (Fig. 7b). The continuous black lines represent the RT results. To compare with flow over a smooth wall, i.e. without the roughness transition, the results from the D simulations are shown as the blue dashed lines. Clearly, the roughness transition introduces a large velocity defect that results in an internal boundary layer, whose depth is indicated as $\delta _i$. In the next section it will be explained how it is determined.

The PR simulations are presented by a single temporally- and spatially-averaged profile of the streamwise velocity component; it is shown at each downstream location (red dash-dotted lines in Fig. 7) in order to investigate to what extent the flow in the RT simulations has adapted to the increased roughness and when it can be considered fully developed. For neutral conditions at the 24th street the velocity defect has smoothly blended with the outer flow velocity profile such that the full velocity profile is nearly indistinguishable from the PR results. This suggests the mean flow has practically adapted to the surface roughness. However, for stable conditions the velocity profile of the RT simulation at the 24th street does not (yet) agree with the velocity profile of the PR simulation. Near the canopy there is a layer with increased shear compared to the smooth-wall flow that reaches up to the internal boundary-layer height. Above that region the velocity profile follows the smooth-wall profile. In contrast, the velocity profile of the PR simulation does not show these two regions, but a single smooth profile instead.

Fig. 7

Streamwise development of $\langle \overline{u}\rangle$ for, a neutral conditions, and b stable conditions

In Fig. 8a the corresponding temperature profiles are plotted showing that inside the canopy in the RT and PR simulations $\partial \langle \overline{\theta }\rangle / \partial z$ is decreased compared to the D simulation. In addition, in the internal boundary layer in the RT simulation $\langle \overline{\theta }\rangle$ is smaller than in the D simulation, while above the internal boundary layer $\langle \overline{\theta }\rangle$ is similar to values found in the D simulation. As a consequence of these velocity and temperature profiles in the RT simulation the gradient Richardson number, $Ri_\mathrm{grad}$ (Eq. 7), is decreased in the internal boundary layer compared to the D simulation, as shown in Fig. 8b. The D results show a nearly constant $\langle Ri_\mathrm{grad}\rangle$ of about 0.2 from $z=h=0.1\delta$ up to $z=6h=0.6\delta$, above which $\langle Ri_\mathrm{grad}\rangle$ increases to 0.26. In the results for the PR simulation $\langle Ri_\mathrm{grad}\rangle$ increases approximately linearly from 0.05 at $z=1.3h=0.13\delta$ to 0.24 at the top of the boundary layer ($=10h$). The fact that there are two regions in the RT results—the aforementioned region of low $\langle Ri_\mathrm{grad}\rangle$ in the internal boundary layer and a region above the internal boundary layer with values of $\langle Ri_\mathrm{grad}\rangle$ that correspond to the inflow boundary layer—indicates that for stable conditions the flow field has not yet adapted to the increased surface roughness. Moreover, the streamwise velocity component in the PR simulation for stable conditions differs from the neutral case indicating that also for fully-developed conditions at this bulk Richardson number buoyancy effects are still important.

Fig. 8

Streamwise development of, a $\langle \overline{\theta }\rangle$, and b $\langle Ri_\mathrm{grad}\rangle$ for stable conditions

4.3 Internal Boundary-Layer Growth

There exist several definitions of the internal boundary-layer depth, $\delta _i$ (Garratt 1990). In a study on flow over cubical roughness arrays (Cheng and Porté-Agel 2015) $\delta _i$ is defined as the height at which $\overline{u}$ reaches 99 % of the upstream velocity. However, because the simulated domain has a finite height ($L_z=3\delta$ in the current study and $L_z=1.08\delta$ in Cheng and Porté-Agel (2015)) the flow accelerates due to the blockage by the canopy. Therefore, with their definition, $\delta _i$ depends on the domain height that is used, which is undesirable. In the present study $\delta _i$ is found by subtracting the mean streamwise velocity component found in the D simulations (smooth wall) from the mean streamwise velocity component found in the RT simulations: ${\varDelta }\langle \overline{u}\rangle = \langle \overline{u}\rangle _{RT} - \langle \overline{u}\rangle _{D}$, and $\delta _i$ is defined as the height at which the vertical gradient of ${\varDelta }\langle \overline{u}\rangle$ reaches zero. This approach—and probably any method using the gradient of $\overline{u}$ instead of $\overline{u}$ (see also the review by Garratt 1990)—eliminates the difficulty of discerning $\delta _i$ when the flow accelerates above the canopy due to a finite domain height.

The resulting $\delta _i$ is shown in Figs. 7 and 8 by circles. For stable conditions $\delta _i$ grows more slowly than for neutral conditions: $\delta _i$ is 14 % smaller at the end of domain. In Cheng and Porté-Agel (2015) nearly the same configuration is considered for neutral conditions only. As expected, $\delta _i$ found in that study is smaller due to the different definition of $\delta _i$. They find $\delta _i$ to be approximately $2.5h-3.0h$ at street 15 compared to 4.2h at the same location in the current results. However, using their definition of $\delta _i$ a value of 3.1h is found at street 15 in the current results. The slight difference that remains could be explained by the smaller domain height used in Cheng and Porté-Agel (2015), making it more prone to acceleration due to blockage by the canopy. However, there are probably also differences due to the wall modelling they apply and the larger Reynolds number they consider (Re based on h and the upstream velocity at $z=h$ is $3\times 10^4$ in Cheng and Porté-Agel (2015) compared to $3.2\times 10^3$ (neutral) and $4.3\times 10^3$ (stable) in the current results).

Furthermore, the full boundary-layer depth, $\delta$, is also shown in Fig. 7. The results for stable conditions show that at the 24th street $\delta$ is 4 % smaller than for neutral conditions, while for the imposed flow at the inlet $\delta$ is the same for both cases.

4.4 Turbulence Kinetic Energy Budget

Fig. 9

Vertical profiles of resolved TKE budget terms scaled with total production at each height. a, c and e Neutral conditions (indicated by (n)). b, d and f Stable conditions (indicated by (s)). a and b D simulations. c and d RT simulations, street 23 ($x=47h$). e and f PR simulations. The horizontal dashed line represents $\delta _i$

To investigate further the effects of stratification on flow over a roughness transition all terms in the mean resolved turbulence kinetic energy (TKE) budget are considered for the D, RT and PR simulations. The equation governing the mean resolved TKE can be found by multiplying the Navier–Stokes equations by $u_i$, applying temporal averaging and subtracting the kinetic energy of the mean flow. The result of these operations is the equation for $\frac{1}{2}\overline{u_i'u_i'}$,

$$\begin{aligned} \begin{aligned} \overbrace{\overline{u}_j\frac{\partial \tfrac{1}{2}\overline{u_i'u_i'}}{\partial x_j}}^{A} =&\overbrace{-\overline{u_j'\frac{\partial {\varPi }'}{\partial x_j}}}^{T_p} \overbrace{-\frac{\partial }{\partial x_j}\left( \tfrac{1}{2}\overline{u_i'u_i'u_j'}\right) }^{T_t} \overbrace{+\frac{\partial }{\partial x_j}\left( 2\nu \overline{u_i'S_{ij}'}\right) }^{T_v} \overbrace{-\frac{\partial }{\partial x_j}\left( \overline{u_i'\tau _{ij}'}\right) }^{T_{sgs}}\\&\underbrace{+ \frac{g}{\theta _0}\overline{u_i'\theta '}\delta _{i3}}_{P_{b}} \underbrace{-\overline{u_i'u_j'}\overline{S}_{ij}}_{P_t} \underbrace{-2\nu \overline{S_{ij}'S_{ij}'}}_{D_v} \underbrace{+ \overline{\tau _{ij}'S_{ij}'}}_{D_{sgs}}, \end{aligned} \end{aligned}$$

(10)

where A represents advection by the mean flow, $T_p$ is the transport by pressure fluctuations, $T_t$ is the transport by turbulent velocity fluctuations, $T_v$ is the transport by viscous stresses, $T_{sgs}$ is the transport by SGS stresses, $P_{b}$ is the production/destruction by buoyancy fluctuations, $P_t$ is the production by shear, $D_v$ is the resolved viscous dissipation and $D_{sgs}$ is the SGS dissipation, which represents the transfer of energy from resolved scales to subgrid scales. Figure 9 shows the vertical profiles of these terms for the D, RT and PR simulations, where at each vertical position the data are scaled with the total production. The graphs in Fig. 9a, c, e are for neutral conditions and the graphs in Fig. 9b, d, f are for stable conditions. Figure 9a, b contain the D results, Fig. 9c, d contain the RT results at street 23, and Fig. 9e, f show the PR results. Note that $T_{sgs}$ has been added to $T_t$ and $D_{sgs}$ has been added to $D_v$. $T_{sgs}$ is found to be negligible throughout the flow field except in the first cells near to the walls, where it is the same order of magnitude as $T_t$. $D_{sgs}$ is around 40 % of the total dissipation, which implies that still 60 % of the TKE dissipation is resolved.

The results for the D simulations show that the main difference between neutral and stable conditions is that for $z>h$ the buoyancy destruction term, $P_{b}$, is over 21 % of the total destruction of TKE for the stable case. Below $z=h$ $P_{b}$ decreases to zero. In addition, in stable conditions advection by the mean flow and transport due to turbulent velocity fluctuations are reduced. In the region $z=1h-6h$ the TKE budget can be approximated by considering the production, dissipation and buoyancy destruction terms only.

The RT results at street 23 show that above the internal boundary layer the results are similar to the results from the D simulations. This shows that above $z=\delta _i$ the roughness transition is not (yet) felt. The profiles just below $z=\delta _i$ bear a strong resemblance to the upper regions ($z>6h$) of the D and RT cases, which confirms the existence of an internal boundary layer. For stable conditions the $P_{b}$ term shows a clear change at $z=\delta _i$, below which it decreases to almost zero at the canopy height. The fact that this change occurs exactly at $z=\delta _i$ gives confidence that the applied criterion to find $\delta _i$, as described in Sect. 4.3, is appropriate. Furthermore, it is concluded that in the canopy the profiles for the stable case are almost the same as for the neutral case and the $P_{b}$ term is reduced to below 4 % of the total TKE destruction.

Finally, it is concluded that the PR results for stable conditions show no discontinuity in $P_{b}$, because there is no internal boundary layer. However, the magnitude of $P_{b}$ increases linearly with height up to the top of the boundary layer in contrast to the D simulation where $P_{b}$ is approximately constant. The same behaviour is visible for $\langle Ri_\mathrm{grad}\rangle$ (Fig. 8b).

Fig. 10

Instantaneous concentration released from Source 1 in the $x-z$ plane at $y/h=9$; a neutral conditions; b stable conditions. Logarithmic colour scaling

4.5 Pollutant Dispersion

Emissions from two line sources of passive scalar were considered to investigate the effect of stratification on pollutant dispersion. Source 1 was located above the canopy at $z/h = 3$ and Source 2 was located below the canopy top at $z/h = 0.2$. Both sources were placed 2h in front of the first row of cubes. Figure 10 shows the resulting instantaneous concentration fields in the $x-z$ plane in the middle of the domain for Source 1 for neutral (Fig. 10a) and stable conditions (Fig. 10b). The concentration $c^*$ is normalized by $U_\infty$, h, $L_y$ and the total emission Q: $c=c^*U_\infty h L_y/Q$. The difference in vertical mixing between the two cases is clearly visible since the neutral case shows a meandering plume while in the stable case the plume axis remains at approximately the same vertical position. As a result the concentrations stay high over a larger distance in the stable case. Moreover, because the internal boundary layer grows more slowly in stable conditions entrainment into the urban environment occurs farther downstream; for the domain considered here the average concentration within the volume of each street is higher for the neutral case.

Figure 11 shows the instantaneous concentration fields in the $x-z$ plane in the middle of the domain for Source 2 for neutral (Fig. 11a) and stable conditions (Fig. 11b). Throughout the canopy the average concentration within the volume of each street is in the stable case approximately 85 % higher than the neutral case. The lower streamwise advection velocity component $\overline{u}$ (see Fig. 7) is the main cause of the difference. However, if $c^*$ is scaled with the mean streamwise velocity component at the canopy height concentrations are still 17 % larger than the neutral case. This corresponds exactly to the difference in $\delta _i$ between neutral and stable conditions. In other words, when the emission source is below the canopy top, there are two reasons why stably stratified conditions produce higher canopy concentrations: (1) The streamwise advection is decreased, (2) pollutants are trapped in the internal boundary layer, which grows more slowly than in neutral conditions.

Fig. 11

Instantaneous concentration released from Source 2 in the $x-z$ plane at $y/h=9$; a neutral conditions; b stable conditions. Logarithmic colour scaling

Fig. 12

Streamwise development of the mean street-average vertical pollutant flux, $E_\mathrm{top}$ for Source 2, scaled with the freestream velocity and mean street-average concentration; a advective mass flux; b turbulent mass flux. The SGS flux is included

Finally, we consider the vertical flux of pollutant out of the canopy. For each street the total average vertical mass flux can be defined as

$$\begin{aligned} E_\mathrm{top} = \frac{1}{2h L_y}\int ^{2h}_{0}\int ^{L_y}_{0}\left. \overline{wc}\right| _{z=h} dy\,dx = \langle \overline{w}\overline{c}\rangle _{z=h}+\langle \overline{w'c'}\rangle _{z=h}, \end{aligned}$$

(11)

and to obtain insight into the mechanisms that contribute to the vertical street emission the total mass flux can be split up into a contribution due to mean advection, $\overline{w}\overline{c}$, and a contribution due to turbulent motions, $\overline{w'c'}$. Figure 12 shows the streamwise development of both contributions, with the SGS contribution to the turbulent mass flux included in the results. Its magnitude did not exceed 10 % of the total vertical turbulent mass flux. After approximately seven streets the mean vertical advective flux (Fig. 12a) is slightly negative and negligible compared to the mean vertical turbulent flux (Fig. 12b) in agreement with the results for fully-developed flow reported by Michioka et al. (2014). However, the mechanism of pollutant removal from the canopy in the first seven streets is different because of the increased vertical velocity component, which results in significant advective pollutant flux. Moreover, the results show that stratification does not influence this behaviour, but does cause the vertical turbulent mass flux to decrease.

5 Conclusions

Large-eddy simulations (LES) were used to investigate the effect of stable stratification on flow and pollutant dispersion in a turbulent boundary layer entering a generic urban environment. The applied LES method was validated in Tomas et al. (2015a, b) by comparing with experimental data for flow over a surface-mounted fence and is further validated here for flow over cubical roughness by comparing with experimental results of Castro et al. (2006). At all examined locations the vertical profiles for the mean streamwise velocity component, as well as the mean Reynolds stress, show good agreement and minor discrepancies can be explained.

Subsequently, LES for both neutrally buoyant and stably stratified boundary layers entering a generic urban roughness are performed. The inflow turbulent boundary layers were generated in separate driver (D) simulations. To compare with fully-developed flow two additional simulations (PR) were done using periodic boundary conditions in the horizontal directions.

Regarding the question about how a stratified boundary layer responds to a roughness transition, it is concluded that the surface forces in both neutral and stable conditions become approximately constant after seven streets ($=14h$) downstream from the start of the canopy and that for stable conditions the flow experiences a larger increase in $u_\tau$ than for neutral conditions. Moreover, it is found that for neutral conditions after 24 streets ($=48h$) the mean streamwise velocity component is almost indistinguishable from the results of the PR simulation (fully-developed flow). However, this does not hold for the stably stratified boundary layer that develops more slowly. Investigation of the terms in the TKE budget equation shows that at the end of the simulated domain both the neutral and the stable boundary layer are still adapting to the increased roughness: a clear internal boundary layer is visible in the RT results, above which there are strong similarities with the D simulations.

Furthermore, it is found that in stable conditions at the 24th street the internal boundary-layer depth, $\delta _i$, is 14 % shallower compared to neutral conditions. For neutral conditions $\delta _i$ is compared with LES results from Cheng and Porté-Agel (2015) showing a discrepancy that is related to the criterion used to find $\delta _i$. It is argued that $\delta _i$ based on the gradient of the velocity defect (caused by the urban canopy) is preferable, because it does not depend on the domain height of the LES.

Regarding the issue as to whether or not stratification effects are diminished due to the turbulence generated by the roughness elements, it is concluded that the buoyancy destruction of TKE is indeed reduced in the internal boundary layer (from 21 % of the total loss of TKE above the internal boundary layer to zero at the top of the obstacles). However, the buoyancy destruction term does increase with height inside the internal boundary layer up to the value found in smooth-wall flow. Moreover, at the considered bulk Richardson number also for fully-developed flow buoyancy effects are still important, because the profile of the streamwise velocity component of the PR simulation for stable conditions still differs from the neutral results.

Regarding the effects of the roughness transition and stratification on pollutant dispersion it is concluded that in stable conditions pollutants emitted from a line source at $z=3h$ enter the urban canopy at a location farther downstream than for neutral conditions. This is due to decreased vertical mixing that causes pollutants to be advected farther downsteam before entering the urban canopy. As a consequence average street concentrations for the considered domain are lower for stable conditions.

For pollutants emitted from a line source in front of the canopy close to the ground it is concluded that average street concentrations are 85 % higher for stable conditions. Basically, there are two causes for the increased concentration: (1) The streamwise advection is decreased, (2) pollutants are trapped in the internal boundary layer, which grows more slowly than in neutral conditions. The first can be accounted for if the concentration is normalized by the streamwise velocity component at the top of the canopy, which still results in 17 % higher concentrations than for neutral conditions. This corresponds exactly to the ratio of $\delta _i$ for stable and neutral conditions. This result suggests that average canopy concentrations could be predicted when the average advection velocity and average internal boundary-layer depth are known.

Furthermore, the average vertical emission of pollutant out of each street is considered and it is found that the contribution of the advective pollutant flux is significant for the first seven streets after which the vertical pollutant emission is only governed by the turbulent flux similar to the fully-developed case.

Studies on flow over roughness (transitions) and internal boundary-layer development mostly investigate the effect of various roughness properties such as geometry and obstacle density. For example, Cheng and Porté-Agel (2015) show there is no significant difference in internal boundary-layer development for different cube configurations and densities. (This assumes that their aformentioned criterion used to define $\delta _i$ has no influence on this conclusion.) The results presented here indicate that stable stratification, and probably the characteristics of the upstream flow in general, influences internal boundary-layer development over large distances. Therefore, it is recommended that the scope of future investigations should be expanded to include approaching flow properties.