Moving Beyond Monin–Obukhov Similarity Theory in Modelling Wind-Speed Profiles in the Lower Atmospheric Boundary Layer under Stable Stratification

Abstract

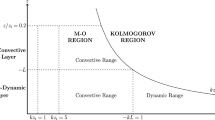
Monin–Obukhov similarity theory (MOST) is commonly used to model the wind-speed profile at altitudes relevant to wind-power production (e.g. 10–200 m). Though reasonably accurate for unstable to weakly stable stratification, this approach becomes less accurate under increasingly stable stratification, largely due to the constant-flux surface layer assumed by MOST becoming shallower than the altitude range of interest. Furthermore, above the surface layer, the Coriolis force has a considerable influence on the wind-speed profile (in particular in the formation of low-level jets) that cannot be modelled using similarity theory. Our goal is to compare the accuracy of alternative extrapolation models that are more physically appropriate above the surface layer. Using data from the 213-m Cabauw meteorological tower in the Netherlands between July 2007 and June 2008, it is shown that MOST is accurate only at low altitudes and low stability, and breaks down at high altitudes and high stability. Local similarity is generally more accurate than MOST across all altitudes and stabilities, though the model requires turbulent flux data at multiple altitudes that is generally impractical. In contrast, a two-layer MOST–Ekman model is found to be comparable to the other models at low stability ranges and considerably more accurate in the high stability range, while requiring only a measure of surface stability and the geostrophic wind.