Skip to main content
SpringerLink
Log in

Talbot quadratures and rational approximations

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

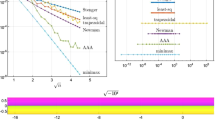
Many computational problems can be solved with the aid of contour integrals containing e z in the integrand: examples include inverse Laplace transforms, special functions, functions of matrices and operators, parabolic PDEs, and reaction-diffusion equations. One approach to the numerical quadrature of such integrals is to apply the trapezoid rule on a Hankel contour defined by a suitable change of variables. Optimal parameters for three classes of such contours have recently been derived: (a) parabolas, (b) hyperbolas, and (c) cotangent contours, following Talbot in 1979. The convergence rates for these optimized quadrature formulas are very fast: roughly O(3-N), where N is the number of sample points or function evaluations. On the other hand, convergence at a rate apparently about twice as fast, O(9.28903-N), can be achieved by using a different approach: best supremum-norm rational approximants to e z for z∈(–∞,0], following Cody, Meinardus and Varga in 1969. (All these rates are doubled in the case of self-adjoint operators or real integrands.) It is shown that the quadrature formulas can be interpreted as rational approximations and the rational approximations as quadrature formulas, and the strengths and weaknesses of the different approaches are discussed in the light of these connections. A MATLAB function is provided for computing Cody–Meinardus–Varga approximants by the method of Carathéodory–Fejér approximation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. I. Aptekarev, Sharp constants for rational approximation of analytic functions, Sb. Math., 193 (2002), pp. 1–72.

    Article  MathSciNet  MATH  Google Scholar 

  2. D. Calvetti, E. Gallopoulos, and L. Reichel, Incomplete partial fractions for parallel evaluation of rational matrix functions, J. Comput. Appl. Math., 59 (1995), pp. 349–380.

    Article  MathSciNet  MATH  Google Scholar 

  3. A. J. Carpenter, A. Ruttan, and R. S. Varga, Extended computations on the ‘1/9’ conjecture in rational approximation theory, in Rational Approximation and Interpolation, P. R. Graves-Morris, E. B. Saff, and R. S. Varga, eds., Lect. Notes Math., vol. 1105, pp. 383–411, Springer, Berlin, 1984.

  4. J. C. Cavendish, W. E. Culham, and R. S. Varga, A comparison of Crank–Nicolson and Chebyshev rational methods for numerically solving linear parabolic equations, J. Comput. Phys., 10 (1972), pp. 354–368.

    Article  MathSciNet  Google Scholar 

  5. W. J. Cody, G. Meinardus, and R. S. Varga, Chebyshev rational approximations to e -x in [0,+∞) and applications to heat-conduction problems, J. Approximation Theory, 2 (1969), pp. 50–65.

  6. E. Gallopoulos, A partial fraction decomposition approach to improved efficiency of some parabolic solvers, Technical report 874, Ctr. for Supercomputing Res. Dev., University of Illinois at Urbana-Champaign, May 1989.

  7. E. Gallopoulos and Y. Saad, On the parallel solution of parabolic equations, Proc. 1989 ACM Internat. Conf. on Supercomputing, pp. 17–28, Heraklion, Greece, 1989.

  8. E. Gallopoulos and Y. Saad, Efficient solution of parabolic equations by Krylov approximation methods, SIAM J. Sci. Statist. Comput., 13 (1992), pp. 1236–1264.

    Article  MathSciNet  MATH  Google Scholar 

  9. I. P. Gavrilyuk and V. L. Makarov, Exponentially convergent parallel discretization methods for the first order evolution equations, Comput. Meth. Appl. Math., 1 (2001), pp. 333–355.

    MathSciNet  MATH  Google Scholar 

  10. I. P. Gavrilyuk and V. L. Makarov, Exponentially convergent algorithms for the operator exponential with applications to inhomogeneous problems in Banach spaces, SIAM J. Numer. Anal., 43 (2005), pp. 2144–2171.

    Article  MathSciNet  MATH  Google Scholar 

  11. A. Gil, J. Segura, and N. M. Temme, Computing special functions by using quadrature rules, Numer. Algorithms, 33 (2003), pp. 265–275.

    Article  MathSciNet  MATH  Google Scholar 

  12. A. A. Gonchar and E. A. Rakhmanov, Equilibrium distributions and degree of rational approximation of analytic functions, Mat. Sb., 134 (1987), pp. 306–352 (English transl. in Math. USSR-Sb. 62 (1989)).

  13. G. H. Halphen, Traité des fonctions elliptiques et de leurs applications, I, Théorie des fonctions elliptiques et de leurs développement en séries, Gauthier-Villars, Paris, 1886 (http://moa.cit.cornell.edu/).

  14. A.-K. Kassam, Solving reaction-diffusion equations ten times faster, Numer. Anal. Rep. NA 03/16, Oxford U. Computing Lab., Oxford, 2003.

  15. A.-K. Kassam and L. N. Trefethen, Fourth-order time-stepping for stiff PDE, SIAM J. Sci. Comput., 26 (2005), pp. 1214–1233.

    Article  MathSciNet  MATH  Google Scholar 

  16. J. D. Lawson and D. A. Swayne, High-order near best uniform approximations to the solution of heat conduction problems, Information Processing 80, pp. 741–746, North-Holland, Amsterdam, 1980.

  17. M. López-Fernández, C. Lubich, C. Palencia, and A. Schädle, Fast Runge–Kutta approximation of inhomogeneous parabolic equations, Numer. Math., 102 (2005), pp. 277–291.

    Article  MathSciNet  MATH  Google Scholar 

  18. M. López-Fernández and C. Palencia, On the numerical inversion of the Laplace transform in certain holomorphic mappings, Appl. Numer. Math., 51 (2004), pp. 289–303.

    Article  MathSciNet  MATH  Google Scholar 

  19. M. López-Fernández, C. Palencia, and A. Schädle, A spectral order method for inverting sectorial Laplace transforms, SIAM J. Numer. Anal., 44 (2006), pp. 1332–1350.

    Article  MathSciNet  MATH  Google Scholar 

  20. Y. Y. Lu, Exponentials of symmetric matrices through tridiagonal reductions, Linear Algebra Appl., 279 (1998), pp. 317–324.

    Article  MathSciNet  MATH  Google Scholar 

  21. C. Lubich and A. Schädle, Fast convolution for nonreflecting boundary conditions, SIAM J. Sci. Comput., 24 (2002), pp. 161–182.

    Article  MathSciNet  MATH  Google Scholar 

  22. Y. L. Luke, The Special Functions and Their Approximations, vol. 1–2, Academic Press, New York, 1969.

  23. Y. L. Luke, Error estimation in numerical inversion of Laplace transforms using Padé approximation, J. Franklin Inst., 305 (1978), pp. 259–273.

    Article  Google Scholar 

  24. A. P. Magnus, Asymptotics and super asymptotics of best rational approximation error norms for the exponential function (the ‘1/9’ problem) by the Carathéodory–Fejér method, in Nonlinear Methods and Rational Approximation, II, A. Cuyt et al., eds., pp. 173–185, Kluwer, Dordrecht, 1994.

  25. W. McLean and V. Thomée, Time discretization of an evolution equation via Laplace transforms, IMA J. Numer. Anal., 24 (2004), pp. 439–463.

    Article  MathSciNet  MATH  Google Scholar 

  26. G. Meinardus, Approximation of Functions: Theory and Numerical Methods, Springer, Berlin, 1967.

  27. C. Moler and C. Van Loan, Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later, SIAM Rev., 45 (2003), pp. 3–49.

    Article  MathSciNet  MATH  Google Scholar 

  28. R. Piessens, On a numerical method for the calculation of transient responses, J. Franklin Inst., 292 (1971), pp. 57–64.

    Article  MathSciNet  MATH  Google Scholar 

  29. R. Piessens, Gaussian quadrature formulas for the numerical integration of Bromwich’s integral and the inversion of the Laplace transform, J. Eng. Math., 5 (1971), pp. 1–9.

    Article  MathSciNet  MATH  Google Scholar 

  30. V. M. Rjabov, Application of Padé approximations to Laplace transformation inversion, Vestn. Leningrad. Univ. Math., 2 (1970), p. 119 (Russian).

    Google Scholar 

  31. A. J. Rodrigues, Properties of constants for a quadrature formula to evaluate Bromwich’s integral, J. Inst. Math. Appl., 18 (1976), pp. 49–56.

    Article  MathSciNet  MATH  Google Scholar 

  32. E. B. Saff and V. Totik, Logarithmic Potentials with External Fields, Springer, Berlin, 1997.

  33. H. E. Salzer, Orthogonal polynomials arising in the numerical evaluation of inverse Laplace transforms, Math. Comput., 9 (1955), p. 164–177.

    Article  MathSciNet  MATH  Google Scholar 

  34. A. Schädle, M. López-Fernández, and C. Lubich, Fast and oblivious convolution quadrature, SIAM J. Sci. Comput., 28 (2006), pp. 421–438.

    Article  MathSciNet  MATH  Google Scholar 

  35. T. Schmelzer and L. N. Trefethen, Computing the gamma function using contour integrals and rational approximations, SIAM J. Numer. Anal., submitted.

  36. A. Schönhage, Zur rationalen Approximierbarkeit von e -x über [0,∞), J. Approximation Theory, 7 (1973), pp. 395–398.

  37. D. Sheen, I. H. Sloan, and V. Thomée, A parallel method for time-discretization of parabolic problems based on contour integral representation and quadrature, Math. Comput., 69 (2000), pp. 177–195.

    MATH  Google Scholar 

  38. D. Sheen, I. H. Sloan, and V. Thomée, A parallel method for time discretization of parabolic equations based on Laplace transformation and quadrature, IMA J. Numer. Anal., 23 (2003), pp. 269–299.

    Article  MathSciNet  MATH  Google Scholar 

  39. R. B. Sidje, Expokit: A software package for computing matrix exponentials, ACM Trans. Math. Softw., 24 (1998), pp. 130–156.

    Article  MATH  Google Scholar 

  40. H. Stahl and V. Totik, General Orthogonal Polynomials, Cambridge University Press, Cambridge, 1992.

  41. A. Talbot, The accurate numerical inversion of Laplace transforms, J. Inst. Math. Appl., 23 (1979), pp. 97–120.

    Article  MathSciNet  MATH  Google Scholar 

  42. N. M. Temme, Special Functions, Wiley, New York, 1996.

  43. L. N. Trefethen, Chebyshev approximation on the unit disk, in Computational Aspects of Complex Analysis, H. Werner et al., eds., pp. 309–323, D. Reidel Publishing, Dordrecht, 1983.

  44. L. N. Trefethen, Matlab programs for CF approximation, in Approximation Theory V, pp. 599–602, Academic Press, Boston, 1986.

  45. L. N. Trefethen, Is Gauss quadrature better than Clenshaw-Curtis?, SIAM Rev., submitted.

  46. L. N. Trefethen and M. H. Gutknecht, The Carathéodory–Fejér method for real rational approximation, SIAM J. Numer. Anal., 20 (1983), pp. 420–436.

    Article  MathSciNet  MATH  Google Scholar 

  47. L. N. Trefethen and J. A. C. Weideman, The fast trapezoid rule in scientific computing, manuscript in preparation.

  48. R. S. Varga, On higher order stable implicit methods for solving parabolic partial differential equations, J. Math. Phys., 40 (1961), pp. 220–231.

    MATH  Google Scholar 

  49. J. Vlach, Numerical method for transient responses of linear networks with lumped, distributed or mixed parameters, J. Franklin Inst., 288 (1969), pp. 99–113.

    Article  Google Scholar 

  50. J. A. C. Weideman, Optimizing Talbot’s contours for the inversion of the Laplace transform, SIAM J. Numer. Anal., to appear.

  51. J. A. C. Weideman and L. N. Trefethen, Parabolic and hyperbolic contours for computing the Bromwich integral, Math. Comput., to appear.

  52. V. Zakian, Properties of IMN and JMN approximants and applications to numerical inversion of Laplace transforms and initial value problems, J. Math. Anal. Appl., 50 (1975), pp. 191–222.

Download references

Author information

Authors and Affiliations

  1. Oxford University Computing Laboratory, Wolfson Bldg., Parks Road, Oxford, OX1 3QD, UK

    L. N. Trefethen & T. Schmelzer

  2. Department of Applied Mathematics, University of Stellenbosch, Private Bag X1, Matieland, 7602, South Africa

    J. A. C. Weideman

Authors
  1. L. N. Trefethen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. A. C. Weideman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. T. Schmelzer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. N. Trefethen.

Additional information

In memory of Germund Dahlquist (1925–2005).

AMS subject classification (2000)

65D30, 41A20

Rights and permissions

Reprints and permissions

About this article

Cite this article

Trefethen, L., Weideman, J. & Schmelzer, T. Talbot quadratures and rational approximations . Bit Numer Math 46, 653–670 (2006). https://doi.org/10.1007/s10543-006-0077-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10543-006-0077-9

Key words

Search

Navigation