Abstract
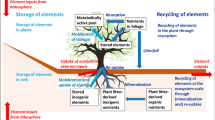
We explore the question of how long elements cycle in terrestrial ecosystems and show that to address this question, a broader conceptual framework is needed that specifies ages and transit times. We calculated age and transit time distributions of five elements in a forest and two grassland ecosystems. Moreover, we assessed how ages and transit times of elements change in various scenarios. Mean age and mean transit time of all elements were smaller in the two grassland ecosystems than in the forest ecosystem due to the smaller element stocks in the grasslands in relation to the inputs. Phosphorus (P) had the largest mean transit time and mean age of all elements in the forest ecosystem (450 and 469 years) as well as in the high elevation grassland (82 and 80 years). Mean ages and mean transit times changed linearly with the stock in one pool. Changes in the internal cycling of elements in the ecosystem that did not imply the introduction of another pool had no effect on age and transit time. However, the introduction of a stable P pool in the mineral soil led to a divergence of mean transit time and mean age of P. Taken together, based on the probabilistic approach proposed here, we were able to precisely calculate not only the mean times elements need to transit different ecosystems and the ages they reach while cycling the ecosystems, but also the probability distribution of ages and transit times.






Similar content being viewed by others
References
Aerts R, Chapin FS (1999) The mineral nutrition of wild plants revisited: a re-evaluation of processes and patterns. Adv Ecol Res 30:1–67
Agren GI, Bosatta E (1996) Theoretical ecosystem ecology: understanding element cycles. Cambridge University Press, Cambridge
Anderson DH (1983) Compartmental modeling and tracer kinetics. Lecture Notes in Biomathematics Vol. 50. Springer, Berlin Heidelberg
Attiwill PM, Adams MA (1993) Nutrient cycling in forests. New Phytol 124(4):561–582
Bolin B, Rodhe H (1973) A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 25(1):58–62
Cleveland CC, Houlton BZ, Smith WK, Marklein AR, Reed SC, Parton W, Del Gosso SJ, Running SW (2013) Patterns of new versus recycled primary production in the terrestrial biosphere. Proc Natl Acad Sci 110(31):12733–12737
Davies JAC, Tipping E, Rowe EC, Boyle JF, Graf Pannatier E, Martinsen V (2016) Long-term P weathering and recent N deposition control contemporary plant-soil C, N, and P. Glob Biogeochem Cycles 30(2):231–249
Finn JT (1976) Measures of ecosystem structure and function derived from analysis of flows. J Theor Biol 56(2):363–380
Frissel MJ (ed) (1978) Cycling of mineral nutrients in agricultural ecosystems. Development of Agricultural Management. Elsevier, New York
Jacquez JA, Simon CP (1993) Qualitative theory of compartmental systems. SIAM Rev 35(1):43–79
Leguerrier D, Bacher C, Benoît E, Niquil N (2006) A probabilistic approach of flow-balanced network based on Markov chains. Ecol Model 193(3):295–314
Liang C, Cheng G, Wixon DL, Balser TC (2011) An absorbing markov cChain approach to understanding the microbial role in soil carbon stabilization. Biogeochemistry 106(3):303–309
Luo Y, Weng E (2011) Dynamic disequilibrium of the terrestrial carbon cycle under global change. Trend Ecol Evol 26(2):96–104
Manzoni S, Katul GG, Porporato A (2009) Analysis of soil carbon transit times and age distributions using network theories. J Geophys Res 114:G04025
Metzler H, Sierra CA (2018) Linear autonomous compartmental models as continuous-time Markov chains: transit-time and age distributions. Math Geosci 50(1):1–34. https://doi.org/10.1007/s11004-017-9690-1
Metzler H, Müller M, Sierra CA (2018) Transit-time and age distributions for nonlinear time-dependent compartmental systems. Proc Natl Acad Sci 115(6):1150–1155. https://doi.org/10.1073/pnas.1705296115
Neuts MF (1981) Matrix-geometric solutions in stochastic models: An algorithmic approach. Courier Corporation
Odum EP (1969) The strategy of ecosystem development. Science 164:262–270
Parton WJ, Neff J, Vitousek P (2005) Modelling phosphorus, carbon and nitrogen dynamics in terrestrial ecosystems. In: Turner B, Frossard E, Baldwin D (eds) Organic phosphorus in the environment. CABI, Oxford, pp 325–348
Patten BC, Higashi M (1984) Modified cycling index for ecological applications. Ecol Model 25(1–3):69–83
Rasmussen M, Hastings A, Smith MJ, Agusto FB, Chen-Charpentier BM, Hoffman FM, Jiang J, Todd-Brown KEO, Wang Y, Wang Y-P, Luo Y (2016) Transit times and mean ages for nonautonomous and autonomous compartmental systems. J Math Biol 73(6):1379–1398
Rastetter EB, Shaver GR (1992) A model of multiple-element limitation for acclimating vegetation. Ecology 73(4):1157–1174
Rodhe H (2000) Modeling biogeochemical cycles. In: Jacobson MC, Charlson RJ, Rodhe H, Orians GH (eds) Earth system science: from biogeochemical cycles to global change. Academic Press, Cambridge, pp 62–84
Sierra CA, Müller M (2015) A general mathematical framework for representing soil organic matter dynamics. Ecol Monogr 85:505–524
Sierra CA, Müller M, Trumbore SE (2014) Modeling radiocarbon dynamics in soils: SoilR version 1.1. Geosci Model Dev 7(5):1919–1931
Sierra CA, Müller M, Metzler H, Manzoni S, Trumbore SE (2017) The muddle of ages, turnover, transit, and residence times in the carbon cycle. Global Change Biol 23(5):1763–1773
Spohn M (2016) Element cycling as driven by stoichiometric homeostasis of soil microorganisms. Basic Appl Ecol 17(6):471–478
Sterner RW, Elser JJ (2002) Ecological stoichiometry: the biology of elements from molecules to the biosphere. Princeton University Press, Princeton
Thompson MV, Randerson JT (1999) Impulse response functions of terrestrial carbon cycle models: method and application. Global Change Biol 5(4):371–394
Uhlig D, Schuessler JA, Bouchez J, Dixon JL, von Blanckenburg F (2017) Quantifying nutrient uptake as driver of rock weathering in forest ecosystems by magnesium stable isotopes. Biogeosciences 14(12):3111
Vitousek P (2004) Nutrient cycling and limitation: Hawaii as a model system. Princeton University Press, Princeton
Acknowledgements
Both authors thank the Emmy-Noether program of the German Research Foundation for funding. MS also thanks the German Research Foundation for funding the project SP 1389/5-1 in the priority program 1803 “Earthshape”.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Melany Fisk.
Electronic supplementary material
Below is the link to the electronic supplementary material.
10533_2018_452_MOESM2_ESM.pdf
Supplementary material 2 (TIFF 283 kb). Figure S0 Mean age and mean transit time of nitrogen, phosphorus and potassium in a high elevation moorland sheep farming system and in an improved hill sheep farming system calculated based on the data presented in Fig. 2. The dashed line has a slope of 1
10533_2018_452_MOESM3_ESM.png
Supplementary material 3 (PNG 122 kb). Figure S1 Stocks and rates of phosphorus (P) in a Eucalyptus regnans forest in south-eastern Australia. Pools are given in bold, fluxes are given in italics, and inputs and outputs of the total ecosystem are marked in red. Fluxes and stocks are the same as in Fig. 1 but two addition P pools (intermediate available P and hardly available P) that exchange P with the easily available P pool are added to the minerals soil
10533_2018_452_MOESM4_ESM.pdf
Supplementary material 4 (PDF 32 kb). Figure S2 Age of (A) nitrogen, (B) phosphorus, (C), potassium, (D) magnesium, and (E) calcium in the vegetation, in the organic layer, and in the mineral soil in a temperate Eucalyptus regnans forest. The mean age of each element is indicated by a dashed line and is given in brackets
10533_2018_452_MOESM5_ESM.pdf
Supplementary material 5 (PDF 11 kb). Figure S3 Age of (A) nitrogen, (B) phosphorus, and (C) potassium in the sheep, in the vegetation and in the mineral soil in a high elevation moorland sheep farming ecosystem. The mean age of each element is indicated by a dashed line and is given in brackets
10533_2018_452_MOESM6_ESM.pdf
Supplementary material 6 (PDF 10 kb). Figure S4 Age of (A) nitrogen, (B) phosphorus, and (C) potassium in the sheep, in the vegetation and in the mineral soil in an improved hill sheep farming ecosystem. The mean age of each element is indicated by a dashed line and is given in brackets
10533_2018_452_MOESM7_ESM.pdf
Supplementary material 7 (PDF 19 kb). Figure S5 Age of (A) nitrogen, (B) phosphorus, and (C) potassium in the sheep, in the vegetation and in the mineral soil in an improved hill sheep farming ecosystem in the original case study and in two scenarios. The mean age of each element is indicated by a dashed line and is given in brackets
Rights and permissions
About this article
Cite this article
Spohn, M., Sierra, C.A. How long do elements cycle in terrestrial ecosystems?. Biogeochemistry 139, 69–83 (2018). https://doi.org/10.1007/s10533-018-0452-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10533-018-0452-z