Introduction

Biotic invasions of plant and animal pests and pathogens pose serious threats to indigenous biodiversity, ecosystem functions and services, and agricultural productivity (Gurevitch and Padilla 2004; Julia et al. 2007; Mack et al. 2000; Pimentel et al. 2005; Vitousek et al. 1997; Yemshanov et al. 2009). Consequently, large annual investments are made in the management of invasive species worldwide (Pimentel et al. 2001). Eradication has been demonstrated to be an effective long-term solution on islands (Donlan et al. 2003; Keitt and Tershy 2003; Keitt et al. 2011; Russell et al. 2009; Towns and Broome 2003), but the new frontier in invasive species management is eradication over ever-larger land masses (Pennisi 2016; Russell et al. 2015). Broadscale eradications are expensive and logistically complicated because large areas occupied by pests or diseased animals cannot all be treated at one time (Homans and Horie 2011). Broadscale campaigns can take years or decades of planning and implementation. A lack of financial resources has been identified as a major impediment to broadscale eradications for environmental outcomes, despite their increasing feasibility (Simberloff 2014). Minimising demands on funding is contingent on implementing a robust quantitative methodology for identifying optimal cost-efficient strategies for allocating resources over space and time.

Various broadscale eradications are currently underway or in the planning stages around the world. Progress made to date in the eradication of bovine tuberculosis (BTB) from wildlife and livestock in New Zealand demonstrates that broadscale eradication is possible (Livingstone et al. 2015; Nugent et al. 2015). Significant progress (and some setbacks) have been experienced in the attempted eradication of red imported fire ants (Solenopsis invicta) from approximately 380,000 ha around Brisbane, Queensland, Australia since efforts began in 2001 (Keith and Spring 2013; Moloney and Vanderwoude 2002). A further two examples in the planning and proposal stages, respectively, are the proposed joint venture between Argentina and Chile to eradicate beavers (Castor canadensis) from Tierra del Fuego (Menvielle et al. 2010), and the eradication of mammalian wildlife pests from New Zealand (Pennisi 2016; Russell et al. 2015) such as rats (Rattus rattus), stoats (Mustela erminea) and brushtail possums (Trichosurus vulpecula). All four are ambitious goals requiring years of investment, but as yet none of them is based on an analytical framework for assessing success at regional or country-wide scales that incorporates rigorous probability theory, biology (including epidemiology) and socio-economic constraints. In addition to providing an objective basis for decision making, a formal analytical structure for broadscale eradications would foster realistic and consistent expectations among managers, funders and the public. While the above examples and numerous other eradication programmes differ in many respects, they are unified by the spatiotemporal complexities they face and would benefit from a common analytical decision framework for assessing progress and declaring success.

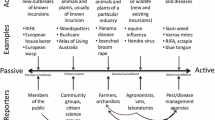
Large areas subject to eradication plans are frequently sub-divided into management zones (MZ), often by necessity due to operational constraints over big areas. In the case of BTB in New Zealand, the disease management agency, OSPRI, controls the disease within a MZ by reducing the localised abundance of the maintenance host (brushtail possums; Coleman and Caley 2000; Jackson et al. 1995; Morris et al. 1994; Nugent et al. 2015) and conducts surveillance to confirm local disease freedom. This is done progressively over space and time across ~700 MZs, which typically average ~100 km2 in size. In each MZ, a quantitative tool is used to calculate a probability that the disease has been removed from the MZ given no disease detections (Anderson et al. 2013, 2015). Once a MZ is declared ‘free’ of disease, financial resources are reallocated to other MZs, and the operation progresses over all areas at risk from wildlife vectors. This approach is depicted in Fig. 1 for the hypothetical eradication of an invasive pest or disease, on a year-by-year basis commencing in 2016. Within this approach, we apply the term ‘freedom’ to refer to the complete removal of a disease or pests from a MZ; while the term ‘eradicated’ is reserved for the broadscale area of interest (a ‘region’ or entire country). In general terms, the MZs of relevance should be defined according to the operational capacity of the eradication team, and by pest or vector biology. Each MZ should be several times larger than the expected ranging area of the target species, which should reduce the risk of reinvasion into MZs previously declared free of disease or pests. However, it should be small enough for management to be able to remove pests and conduct follow-up surveys in a short period of time—relative to the total duration of the broadscale eradication operation.

Fig. 1
figure 1

The spatiotemporal progression of a hypothetical broadscale eradication operation (black arrows), over a square-shaped region, that begins in the northwest of the region in 2016 and finishes in the southeast in 2034. Each square represents a spatial region for control and the number in each represents the year that the region is controlled. Surveillance devices or search effort are allocated to the surveillance unit. Stage I freedom is an operational decision at the management-zone level that allows re-allocation of resources to other management zones and progresses the operation across the landscape. Stage II entails on-going surveillance in management zones passed out of Stage I to identify erroneous freedom declarations, and to declare the entire broadscale area eradicated. Confirmation of eradication in Stage II may extend well beyond 2034

Full size image

Given that the probability of successful freedom in each MZ will always be less than 100%, there is a risk that freedom of a MZ could be wrongly declared. On-going surveillance is required to detect these failures until the entire broadscale area can be declared eradicated. Importantly, declaring freedom over many individual MZs does not necessarily equate to high confidence that the entire broadscale area has been successfully eradicated. Consider the following hypothetical situation in which 10 MZs were independently declared free of pests or disease with a 0.95 probability of freedom. One might be tempted to conclude that—because all MZs have been declared free with a high level of confidence—we can be equally confident that the whole area has been successfully eradicated. However, assuming a correct probability model, each MZ has a 0.05 chance of having a surviving residual population (i.e. erroneous freedom declaration). Therefore, the probability that at least one of the 10 MZs still harbours a viable population is compounded to 0.40 (0.40 = 1 − (1 − 0.05)10), equating to an overall probability that is not much better than a coin toss.

Existing pest-management optimisation models have not yet explicitly incorporated the complexities inherent in broadscale eradications. Prior to an incursion, simulation studies have shown that optimal resource allocation to incursion-prevention and eradication (at local scales) depends on damage and management costs, detection and control efficiency, invasion risk, and pest population growth rates (Bogich et al. 2008; Epanchin-Niell et al. 2012, 2014; Guillera-Arroita et al. 2014; Hauser and McCarthy 2009). The optimisation modelling of incursion detection and eradication of gypsy moth (Lymantria dispar) in the western U.S.A. is a broadscale problem, but eradication is attempted and declared only at local scales (Bogich et al. 2008; Liebhold and Bascompte 2003). The additional complexities discussed in our paper would have to be addressed if management aimed to declare gypsy moths eradicated from the entire state of California, which is unlikely to be feasible due to high propagule pressure (see Bomford and O’Brien 1995). Once an incursion has occurred, simulation studies have shown that the optimal spatial and temporal allocation of control effort will be influenced by the spatial distribution of the population, and its rates of growth and spread (Baker 2017; Baker and Bode 2016; Bonneau et al. 2016).

Within the context of broadscale eradications, there is a need for an objective decision-making framework for assessing progress at the MZ level and ultimately for declaring eradication success over the entire area of interest. More specifically, after control has occurred and surveillance is no longer detecting individual pests, how much additional surveillance effort is required to be confident that (1) a MZ is free of pests so that resources can be allocated to other MZs, and (2) the entire broadscale area of interest has been successfully eradicated so that resources can be allocated to other environmental issues. Such a framework could result in large cost savings by reducing the risks that (1) not enough effort is invested and freedom/eradication is prematurely declared, or (2) more money is spent than is necessary to achieve freedom/eradication, thus detracting funding from the overall goal.

In this paper we describe a two-stage approach for analysing surveillance data to assess progress and ultimately declaring success of broadscale eradications. This entails quantifying the probability of disease or pest freedom and declaring success at the MZ level (Stage I), and over the entire broadscale area (Stage II). Importantly, the data models are only applicable when surveillance results in non-detections. We additionally demonstrate how models can also be used in the planning of an eradication operation to identify cost-efficient strategies, and to estimate operational costs and duration. Integral to planning are bio-economic models for Stages I and II, because these identify optimal cost-efficient surveillance strategies as well as decision points at which to declare success. The fundamental features can be easily adapted to meet the specific needs of any broadscale eradication program.

We developed a computer algorithm that applied these bio-economic models to a hypothetical region of 1750 km2 (approximately the area of Stewart Island, New Zealand [(47°S, 168°E)]). A region of this size is likely to be sub-divided into several individual MZs. A region of this size is likely to be sub-divided into several individual MZs. In Stage I we explored 10,000 potential surveillance strategies within a single MZ and addressed the following four questions: (1) what would be the optimal cost-efficient balance between local surveillance intensity and proportion of the MZ subjected to surveillance?; (2) how many years would be required to complete Stage I using the optimal strategy?; (3) what would be the optimal stopping probability of freedom?; and (4) how sensitive would the optimal strategy to variation in the re-start cost be (i.e. re-control and re-survey cost) if MZ freedom was erroneously declared? Next, we further explored the 10,000 surveillance strategies and re-addressed questions (1), (2) and (3) respective to Stage II. In Stage II we did not optimise the stopping probability of broadscale eradication, because declaration of success will be the final management decision and the risk of failure must be agreed upon and fixed in advance. The bio-economic optimisation in Stage I balances type I and II error rates, whereas in Stage II the type I error rate is fixed.

The decision framework assumes that eradication is the chosen management objective, MZs and the total spatial extent are defined, and that control and surveillance techniques are established. We do not address feasibility and the bio-economic trade-offs of eradication versus sustained control in perpetuity (see Baxter et al. 2008; Panetta and Cacho 2014; Parkes and Panetta 2009; Rout et al. 2011). However, the bio-economic models presented here could be used as tools to inform a feasibility analysis or the decision to either eradicate or manage to near-zero density (control in perpetuity).

Methods: Stage I

Stage I operates at the MZ level and begins when the wildlife pest or disease is either known to be present, or confidence in its absence is low. In each of the MZs, pest or disease-vector control is continued until there is no evidence of survivors or residual disease (Animal Health Board 2009; Nugent et al. 2015). For BTB in New Zealand, this is currently accomplished with a combination of trapping and toxin application to control populations of the main BTB wildlife maintenance host and vector, the brushtail possum (Warburton and Livingstone 2015). Concurrent or subsequent surveys are used to detect surviving pests or residual disease. When surveillance fails to find pests or disease (i.e. all negative results), those data are used to quantify the probability of freedom given negative surveillance (i.e. no detections). When management declares a MZ free, the MZ is advanced to Stage II (described below), which may occur in a spatial and temporal progression (Fig. 1).

Analysis of surveillance data is organised in a nested fashion (Fig. 1). At the finest scale is the surveillance unit (SU) for which the probability of detection of a single individual pest (or infected animal in the case of disease) is estimated (Pd—the sensitivity of surveillance at the SU level). The Pd can be estimated for a non-spatial or spatial SU. Surveillance of disease in wildlife can be used to illustrate a non-spatial example in which an individual animal is the SU and multiple animals are tested for disease (Oidtmann et al. 2013). In that case, Pd is the probability of detecting the disease in an individual with a specific testing regime given that the animal is infected. For a spatial SU, (e.g. spatially defined area of 1 ha), Pd is the probability of detecting the presence of an individual pest or infected animal given that one or more are present. Pd is a function of search-effort and may be estimated using a model that quantifies change in Pd resulting from change in search effort (e.g. deployment time and number of devices, disease testing regime, etc). The SU is nested within the MZ (Fig. 1). There will necessarily be multiple SUs per MZ when non-spatial units are employed for disease eradication. However, the number of spatial SUs per MZ will vary from one (Ramsey et al. 2009) to many thousands (Anderson et al. 2013) depending on the modelling framework and the movement attributes of the target organism relative to the area of the MZ.

Multiple sources of data could be used, when available, to estimate Pd (Anderson et al. 2013, 2015). For BTB in New Zealand, this can include direct surveillance of possums or of non-maintenance wildlife hosts that can act as sentinels for disease presence/persistence in the maintenance host (Nugent 2011). The use of sentinels (or Judas animals) can also be used for non-disease problems (Ramsey et al. 2009). A wide range of active and passive detection devices can also be employed; such as traps, chew-track cards (Sweetapple and Nugent 2011), camera traps, tracking tunnels, public reports and citizen surveillance, or remote sensing (e.g. for beavers on Tierra del Fuego).

From here on we generalise an ‘infected SU’ to indicate an incomplete or failed removal of a disease or pest from a MZ. The \(Pd_{i}\) for all surveyed SU i within MZ j are then aggregated to calculate MZ-level sensitivity (Se j ), or the probability of detecting at least one infected SU given the population of SUs is infected at a set ‘design prevalence’ \(\left( {P_{u}^{*} } \right)\). We use a binomial approximation to the hypergeometric sampling process with imperfect sensitivity to calculate \(Se_{j}\) (Anderson et al. 2013; Cameron and Baldock 1998; Martin et al. 2007):

$$Se_{j} = 1 - \left( {1 - PdAve_ {j} Prp_{j} }\, \right)^{{P_{u}^{*} }}$$
(1)

where \(PdAve_{j}\) is the average \(Pd_{i}\) across surveyed SUs in MZ j , and \(Prp_{j}\) is the proportion of SUs surveyed in MZ j .

\(P_{u}^{*}\) is a required parameter for the probability calculation (Eq. 1) because it defines the number of infected SUs available to be detected by the surveillance system. Intuitively and quantitatively, it is easier to detect one of many infected SUs than it is a single infected SU. \(P_{u}^{*}\) is analogous to the ‘design prevalence’ used in disease surveillance (Cameron and Baldock 1998; Martin 2008; Martin et al. 2007). The value of \(P_{u}^{*}\) should be set to equal the minimum expected abundance of infected SUs in a given MZ that could give rise to a self-sustaining population (Oidtmann et al. 2013). For example, in the Stage I removal of BTB from a MZ, the wildlife disease-vector population is likely to have been controlled to very low levels. If the disease is present, the absolute number of infected SUs would be low. Further, given the goal is to demonstrate freedom, the \(P_{u}^{*}\) in this context should be set to the minimum number of infected SUs that could be infected (see Anderson et al. 2013). To illustrate a pest-species freedom example, consider that a single surviving pregnant rat could re-seed an entire population on the 1750 km2 Stewart Island, New Zealand. In this case, the \(P_{u}^{*}\) should be set to 1 so that Se j is the probability of detecting a single infected SU in the MZ. The \(P_{u}^{*}\) could be set at a higher value depending on the time since cessation of control, and the rates of pest population growth and spread. For example, in Stage II it could be justified to set \(P_{u}^{*}\) at higher values or allow an increase over time because the post-control population would be expected to increase in size (Bonneau et al. 2016; Shigesada et al. 1995) (see discussion below).

The spatial distribution of pest populations is not expected to be uniform and could follow habitat heterogeneity in the landscape (Hutchinson 1959; MacArthur and Pianka 1966). Surveillance effort will also often be distributed heterogeneously due to habitat selection by individuals in the target population (Baker 2017; Baker and Bode 2016), and logistical constraints. When not all SUs are surveyed within a MZ, then spatial variation in each SU’s risk of infection should be incorporated to improve estimates of Se j (see Anderson et al. 2013; Martin et al. 2007).

The risk of an infected SU persisting will vary across all MZs. Consequently, Bayesian logic is used and a prior probability of freedom, Prior j,t , (Gelman et al. 2004) is incorporated to estimate the posterior probability of freedom given negative surveillance (Anderson et al. 2013; Ramsey et al. 2009) for MZ j at time t (P(Freedom | S −) j,t ):

$$P\left( {Freedom|S^{ - } } \right)_{j,t} = \frac{{P\left( {S^{ - } |Freedom} \right)_{j,t} P\left( {Freedom} \right)_{j,t} }}{{P\left( {S^{ - } |Freedom} \right)_{j,t} P\left( {Freedom} \right)_{j,t} \,+\, P\left( {S^{ - } |Infected} \right)_{j,t} P\left( {Infected} \right)_{j,t} }}$$
(2)

where \(P\left( {S^{ - } |Freedom} \right)_{j,t}\) is the specificity, \(P\left( {Freedom} \right)_{j,t}\) is Prior j,t , \(P\left( {S^{ - } |Infected} \right)_{j,t}\) is 1 − Se j,t , and \(P\left( {Infected} \right)_{j,t}\) is 1 − Prior j,t . In modelling the confirmation of eradication success, the specificity should be increased to 1 (i.e. no false positives) because a positive detection should be thoroughly investigated to confirm the presence of the pest or disease. If pest or disease presence is confirmed, then \(P\left( {Freedom|S^{ - } } \right)_{j,t}\) = 0, indicating that control operations would have to be restarted. Assuming perfect specificity, Eq. 2 is reduced to the following:

$$P\left( {Freedom|S^{ - } } \right)_{j, t} = \frac{{Prior_{j,t} }}{{1 - Se_{j,t} \left( {1 - Prior_{j,t} } \right)}}.$$
(3)

Given negative surveillance outcomes, the prior is then updated with each new surveillance period (e.g. year, season) with the posterior from the preceding year:

$$Prior_{j, t + 1} = P\left( {Freedom|S^{ - } } \right)_{j,t} .$$
(4)

Because of the potential risk of re-introduction (re-invasion) or backfill when attempting broadscale eradications as the operation progresses across the landscape (Fig. 1), the priors can also be discounted by an estimated probability of re-introduction (P(Intro) j ) (Anderson et al. 2013; Martin 2008).

The stopping \(P\left( {Freedom|S^{ - } } \right)_{j,t}\) (Eq. 3) defines the decision point at which a MZ j is declared free. Assuming the model is correct and the stopping \(P\left( {Freedom|S^{ - } } \right)_{j,t}\) is less than 1.0, some MZs could be wrongly declared free, which would entail additional costs to re-control and survey. The rate of erroneous declarations corresponds to the complement of the stopping probability of freedom (1 − stopping probability). The stopping \(P\left( {Freedom|S^{ - } } \right)\) may vary across MZs and should be determined with the Stage I bio-economic model. The optimal cost-efficient stopping probability will be highly dependent on a number of factors, including the cost of control and re-control, the type of surveillance carried out, the cost of surveillance relative to the cost of control, and the surveillance sensitivity (Gormley et al. 2016).

Stage I bio-economic model

The Stage I bio-economic model identifies optimal strategies for deploying surveillance effort over space and time that minimises the total expected costs (Regan et al. 2006). Associated model predictions are an optimal cost-efficient stopping probability of freedom (\(P\left( {Freedom|S^{ - } } \right);\) e.g. 0.70–0.99) and the expected years of surveillance to reach the stopping probability. Stage I may take years to complete in a MZ and because there are potentially many MZs going through Stage I at different times (Fig. 1), it may be necessary to limit the number of years allowed for each MZ to achieve freedom. Two fundamental surveillance/strategy trade-offs, which influence the cost and time to declare freedom in a MZ, are integrated into the model. The first is the balance between the intensity of surveillance within individual SUs (PdAve j ) and the proportion of all SUs in MZ j that are surveyed (\(Prp_{j}\)). Increasing both would increase financial costs but decrease time to freedom declaration. With a fixed budget, an increase in one would require a decrease in the other. The second surveillance-strategy trade-off is the balance between declaring MZ j free at a low stopping probability, or investing more to attain a high probability of freedom. Decreasing the stopping probability of freedom reduces surveillance costs but increases the risk of making an incorrect decision and incurring re-control and additional survey costs.

We developed a generic computer algorithm in the Python programming language (Python Software Foundation 2013; Appendix S1, http://doi.org/10.7931/J22N506H) to illustrate the Stage I bio-economic model over a hypothetical landscape in which a given MZ j was composed of 5000 SUs, each of 1 ha area. These spatial attributes are provided for context, however the model is scale-independent. The bio-economic model was run for 250,000 surveillance strategies in which each had a unique combination of surveillance intensities within SUs (500 values of \(Pd_{i}\)) and proportion of SUs surveyed in MZ j (500 values of \(Prp_{j}\)). Each surveillance scenario was assumed to begin immediately following a pest-population removal operation, (e.g. using toxins and trapping), which resulted in a Prior j,t of 0.70. For each scenario, the model was run for 5 years (after the cessation of control), which was our imposed maximum time allowed to declare freedom in MZ j . The total expected cost of declaring Stage I freedom was calculated for each of the 5 years (details below). The optimal cost-efficient time to declare freedom and the corresponding probability of freedom was determined by the year that had the lowest total expected cost. Consequently, among the 5 years of surveillance, each scenario had a minimum total expected cost and a corresponding number of years of surveillance. The optimal surveillance strategies for MZ j were identified as those within the 0.10 quantile of the total expected cost (i.e. lowest cost).

We explored the sensitivity of optimal cost-efficient strategies to the modelled trade-offs, therefore we present relative rather than absolute costs. Further, we modelled mean values of model parameters and did not incorporate uncertainty. We modelled 500 evenly-spaced values of the intensity of surveillance within a SU (\(Pd_{i}\)) ranging from 0.05 to 0.99 in combination with 500 evenly spaced proportions of SUs surveyed (\(Prp_{j}\)) ranging from 0.05 to 0.99. The number of SUs surveyed was determined by \(Prp_{j}\), and each then received surveillance with sensitivity \(Pd_{i}\). The relationship between \(Pd_{i}\) and the relative financial cost was a function of the effort required to achieve a given \(Pd_{i}\). The \(Pd_{i}\) value for a single search-effort unit (e.g. 1 h searching in a single SU) was 0.05 and had a cost-unit of 1.0 (notionally $1). For each value of \(Pd_{i}\), the required search effort in SU i (SearchEffort i ) and associated cost (Fig. 2) was calculated with the following equation:

Fig. 2
figure 2

The relationship between the probability of detection in SU i (\(Pd_{i}\)) and the associated financial cost. It is based on a single surveillance ‘device’ (or effort unit) resulting in a \(Pd_{i}\) of 0.05

Full size image
$$SearchEffort_{i} = \frac{{log\left( {1 - Pd_{i} } \right)}}{{log\left( {1 - 0.05} \right)}}$$
(5)

The annual surveillance cost (\(SurveillanceCost_{j,t}\)) for MZ j was then the product of the \(Pd_{i}\) cost (\(SearchEffort_{i}\); Eq. 5) and the number of SUs surveyed (as determined by the \(Prp_{j}\) in the given scenario).

For a given \(Pd_{i}\) and \(Prp_{j}\) scenario, the Se j was calculated (Eq. 1) using \(P_{u}^{*}\) of 1 SU. For each scenario we calculated the total expected cost (TEC j,t ) of declaring MZ j free for each of the 5 years (t = 0–4). The TEC j,t was the sum of the accumulated surveillance costs (from year 0 to year t) and the expected starting-over cost (ErrorCost j,t ) if MZ j was wrongly declared free in year t:

$$TEC_{j,t} = \left( {\mathop \sum \limits_{t = 0}^{T} SurveillanceCost_{j,t} } \right) + ErrorCost_{j,t} .$$
(6)

ErrorCost j,t was the combined expected cost of re-control and re-surveillance. This will vary across eradication operations. To assess the influence of relative error costs across scenarios, it is assumed that freedom is declared at time t, and if a pest or disease population persists, it would be detected in Stage II. We devised the following formulation that incorporates the relative costs of re-control and re-surveillance that are discounted by the probability of pest or disease persistence (\(1 - P\left( {Freedom|S^{ - } } \right)_{j,t}\)):

$$ErrorCost_{j,t} = SurveillanceCost_{j,0} \left( {1 + RecontrolFactor} \right) \times \left( {1 - P\left( {Freedom|S^{ - } } \right)_{j,t} } \right)$$
(7)

where \(SurveillanceCost_{j,0}\) was the cost of achieving a \(P\left( {Freedom|S^{ - } } \right)_{j,t}\) equal to 0.95 in a single year using a Prior j,t of 0.70. This was the lowest costing combination of \(Pd_{i}\) and \(Prp_{j}\) that achieved 0.95. In this experimental system, the \(SurveillanceCost_{j,0}\) to obtain 0.95 used \(Pd_{i}\) and \(Prp_{j}\) of 0.90 and 0.98, respectively. RecontrolFactor is a multiplier that makes re-control costs relative to surveillance costs. While every eradication project will have unique surveillance and control costs, the relative difference between these two costs will influence the optimal cost-efficient stopping probabilities of freedom (Gormley et al. 2016). We used values of 400 and 100 to demonstrate model sensitivity to high and low re-control costs relative to surveillance costs. The ErrorCost j,t was weighted by the probability that MZ j is not free of the pest in year t \(\left( {1 - P\left( {Freedom|S^{ - } } \right)_{j,t} } \right)\).

Results: Stage I bio-economic model

In our hypothetical broadscale-eradication modelling, the Stage I surveillance cost for a single year varied 90-fold across the range of \(Pd_{i}\) values (0.05–0.99; Fig. 2). However, when time to declaration of freedom, optimal probability of freedom, and associated costs of re-control and surveillance \(\left( {ErrorCost_{jt} } \right)\) were all factored in, the total expected costs only varied 2.2- and 2.5-fold when \(RecontrolFactor\) was set at values of 400 or 100, respectively (Fig. 3a, d). To illustrate the need to optimise the surveillance effort, if the minimum cost of ‘freedom’ surveillance of a MZ was $100,000, then the worst-case maximum would be $220,000 or $250,000 for high or low \(ErrorCost_{jt}\), respectively.

Fig. 3
figure 3

Two-dimensional images of Stage I bio-economic analysis of 10,000 potential surveillance strategies, in which the colour gradient ranges from low (blue) to high (red-brown). For each value of detection probability (\(Pd_{i}\)) and proportion SUs surveyed (\(Prp_{j}\)), the time to freedom and \(P\left( {Freedom|S^{ - } } \right)_{jt}\) are optimised. Using a high re-control cost (\(RecontrolFactor\) = 400), the top row of images are the optimal values for: a the relative expected costs, b the number of years to declare freedom, and c the optimal threshold probability of freedom \(\left( {P\left( {Freedom|S^{ - } } \right)_{jt} } \right).\) The black contour line is the 0.10 quantile of the total expected cost (a), indicating the range of the most cost-efficient scenarios. The second row presents results of scenarios using \(RecontrolFactor\) = 100: d the relative total expected costs, e duration (the number of years taken) to declare freedom, and f the optimal threshold probability of freedom \(\left( {P\left( {Freedom|S^{ - } } \right)_{jt} } \right)\)

Full size image

The first analysis of the potential Stage I surveillance strategies assumed a relatively high cost of wrongly declaring freedom (\(RecontrolFactor\) = 400; Eq. 7). Results demonstrated that the total expected cost was lowest when the \(Pd_{i}\) was roughly in the range of 0.36–0.70 and the \(Prp_{j}\) was >0.75 (lowest 0.1 quantile; Fig. 3a). The least optimal strategies were those with very low \(Pd_{i}\) and either low or high \(Prp_{j}\) (u-shaped pattern; Fig. 3a). Using the lowest 0.1 quantile of the relative total expected costs, we determined that the optimal number of years over which to conduct surveillance was 2–5 (Fig. 3b). The corresponding cost-optimal stopping probability of freedom ranged from 0.94 to 0.98 (\(P\left( {Freedom|S^{ - } } \right)_{j,t} ;\) Fig. 3c).

Assessment of the Stage I surveillance strategies that assumed a relatively low cost of wrongly declaring freedom (\(RecontrolFactor\) = 100; Eq. 7) resulted in optimal \(Pd_{i}\) and \(Prp_{j}\) ranges of 0.08–0.45 and >0.70, respectively (lowest 0.1 quantile; Fig. 3d). The optimal time to freedom with the low \(RecontrolFactor\) ranged from 1 to 5 years (Fig. 3e). The range of optimal stopping probabilities of freedom was 0.80–0.88, which was much lower than when re-control costs were relatively high.

Methods: Stage II

The objective in Stage II is to provide an on-going estimate of the surveillance sensitivity in MZs declared ‘free’ (advanced out of Stage I). Continued surveillance is needed for two important reasons: (1) to detect any failures at the MZ level so that re-control can be implemented (along with re-commenced surveillance); and (2) to estimate a broadscale-surveillance sensitivity and a corresponding probability of eradication (given negative findings from surveillance effort). Ultimately, a probability of eradication of the entire area can be used to inform a management decision to declare the entire broadscale effort successful.

Recall that in Stage I the Se j is estimated for each MZ j under active surveillance and a corresponding probability of freedom is calculated. In Stage II, a surveillance sensitivity is also calculated for MZ j . The focus in Stage II is making inference on the likelihood of eradication over the broadscale area of interest (e.g. that there are no more beavers on Tierra del Fuego). Inference on the eradication state of the broadscale area can only begin once managers are no longer detecting the pest or disease anywhere and are reasonably confident that eradication has been achieved (i.e. after all surveillance effort returns negative outcomes). At that time, the Stage II surveillance is conducted to calculate MZ-level sensitivities, which are used to estimate a broadscale probability of eradication given negative surveillance. Program funders will likely require a projected eradication achievement date (e.g. 2055 has been set for BTB eradication in NZ; Anonymous 2016), therefore a maximum limit should be set for the number of years that can pass between the time the last MZ was declared free and the total area is declared successfully eradicated.

In Stage II active control of the pest or disease in a given MZ has stopped because the stopping \(P\left( {Freedom|S^{ - } } \right)_{j}\) has been reached. Surveillance methodology will likely differ between Stage I and II. Compared to Stage I, Stage II surveillance will usually be less expensive (per unit of area) and cover much larger areas overall, because all or nearly all of the MZs should be searched over a relatively short period of time (e.g. several years). This requires surveillance models that are capable of incorporating the biology of the organism (e.g. demographic and dispersal rates), epidemiology (in the case of diseases) and multiple sources of low-cost detection data to support quantification of MZ-level sensitivities. The following assumption can be made in Stage II that helps to increase Se j over time: if freedom was erroneously declared in Stage I, the surviving pests or remnant pockets of disease would become more prevalent and widespread with time (Caley et al. 2015, 2017; Ramsey and Efford 2010; Samaniego-Herrera et al. 2013). The implication is that the value for \(P_{u}^{*}\) used in the calculation of Se j in Stage II (Eq. 1) should increase over time as a function of underlying population or epidemiological models (e.g. Keith and Spring 2013; Spring et al. 2017). While a pest population at low density may be expected to grow exponentially (Shigesada et al. 1995), the \(P_{u}^{*}\) rate of increase should be conservative when complete eradication is the goal. In each MZ \(P_{u}^{*}\) should begin to increase at the time of Stage I declaration of freedom, which will result in varying \(P_{u}^{*}\) values across MZs over time in Stage II.

Surveillance models in Stage II should take advantage of data that are readily available at low to no cost. For the example of BTB in New Zealand, regular livestock surveillance data (e.g. slaughterhouse inspection of carcasses for TB lesions) that will be collected in Stage II as a part of standard animal health management can be used to inform the likelihood that disease no longer exists in the sympatric and neighbouring possum populations. Caley et al. (2015) used foxes killed by cars and hunters in Tasmania to parameterise an approximate-Bayesian-computation model (Csilléry et al. 2010) to make inference on the likelihood that foxes were eradicated given that no kills were reported in a set number of years. Passive surveillance is conducted by citizens in the eradication of red imported fire ants in and around Brisbane, Australia (Keith and Spring 2013). The sensitivities of these surveillance systems may be initially low, however, they will increase with time because a surviving pest population would be expected to grow and expand making them easier to detect (Epanchin-Niell et al. 2014). The consequent increase in sensitivities will result in increasing probability of broadscale eradication given negative surveillance. This is the effect of an increased or temporally increasing \(P_{u}^{*}\) in Stage II (Eq. 1).

The Se j is estimated for each MZ (as in Stage I using Eq. 1), and all Se j are then aggregated up to a system sensitivity for the entire broadscale area of interest (SSe). A hypergeometric sampling model to estimate the SSe (Anderson et al. 2013; Cameron and Baldock 1998; Martin et al. 2007) is calculated as follows:

$$SSe_{t} = 1 - \left( {1 - SeZoneAve_{t} *Prp_{t} } \right)^{{P_{z}^{*} }}$$
(8)

where SeZoneAve t is the average Se j,t across all management zones in time period t, Prp t is the proportion of the total number of MZs surveyed at time t, and \(P_{z}^{*}\) is the MZ-level design prevalence. Given that the ultimate goal is eradication, the \(P_{z}^{*}\) should always be set to 1 MZ. The SSe t is then used to calculate the probability of broadscale eradication given negative surveillance:

$$P\left( {Erad|S^{ - } } \right)_{t} = \frac{{Prior_{t} }}{{1 - SSe_{t} \left( {1 - Prior_{t} } \right)}}$$
(9)

where Prior t is the prior probability that the entire broadscale area of interest has been successfully eradication. The broadscale prior differs from Prior j,t (Eq. 3), which is the Stage I prior probability of freedom in a given MZ.

The stopping \(P\left( {Erad|S^{ - } } \right)_{t}\) for the entire area of interest should be set high (e.g. >=0.95), as it will be the basis for the final decision to declare eradication success. Once Stage II eradication is declared the programme and funding will stop, the probability of detecting a persisting population will be greatly decreased, and this is why we advocate that the stopping \(P\left( {Erad|S^{ - } } \right)_{t}\) should be set a priori and not as a function of our bio-economic model (as in Stage I). A decision model for setting a stopping \(P\left( {Erad|S^{ - } } \right)_{t}\) is possible (Regan et al. 2006) but problematic for two reasons. First, it requires monetising the cost of erroneously declaring eradication, which is difficult or impossible to ecological or biodiversity costs (Holmes et al. 2015). Second, systematic surveillance to detect survivors after eradication has been declared must be conducted, which defeats the purpose of declaring eradication and reallocating resources.

Stage II bio-economic model

We next developed a computer algorithm for Stage II that closely resembled that of Stage I to illustrate the optimization of surveillance strategies to minimised the total expected costs to achieve a \(P\left( {Erad|S^{ - } } \right)\) of 0.95 (Appendix S2, http://doi.org/10.7931/J22N506H). As in Stage I, we modelled local intensity and spatial extensiveness of surveillance effort (\(Pd_{ave, j}\) and \(Prp_{j}\) in Eq. 1) and associated costs. However, the value of \(Pd_{i}\) for a single search-effort unit (e.g. 1 h searching in SU i ) was 0.01 (as opposed to 0.05 in Stage I). This was done to model the likely case that low cost surveillance would be utilised in Stage II, which correspondingly would have a relatively low sensitivity. As noted above, this would increase the financial feasibility of conducting surveillance over most of the full area of interest in a relatively short period of time.

We modelled 500 values of \(Pd_{i}\) ranging from 0.01 to 0.99, and 500 proportions of SUs surveyed (\(Prp_{j}\)) ranging from 0.01 to 0.99. All MZs were surveyed and received identical surveillance, as defined by the scenario. To demonstrate the model, the prior probability of eradication over the entire area was set at a deliberately low initial level of 0.25. The initial \(P_{u}^{ * }\) was 1 SU but increased with the following logistic growth model:

$$\frac{{dP_{u}^{ * } }}{dt} = rP_{u}^{ * } \left( {\frac{{K - P_{u}^{ * } }}{K}} \right)$$
(10)

where the rate of increase (r) was set to 1 cell year−1, and the maximum level of \(P_{u}^{ * }\) (K) and was set to 2% of the total number of SUs in a MZ (i.e. 5000 SUs × 0.02 = 100 SUs). Any growth model could be applied to \(P_{u}^{ * }\), or it could remain constant. We used parameters to illustrate a fast growing and dispersing population, such as Rattus rattus or Mustela erminea. The number of infested cells should plateau at a conservatively low level because eradication is the goal. To simplify the bio-economic optimisation modelling, all MZs began Stage II at the same time resulting in equivalent \(P_{u}^{ * }\) values across MZs. In reality, MZs will vary in the initiation time of Stage II, and \(P_{u}^{ * }\) values will differ across MZs.

We set a maximum of 15 years for the time between all MZs declared free and the achievement of the stopping probability of broadscale eradication of 0.95. The optimal time to the stopping probability was a trade-off between high-cost surveillance (high \(Pd_{i}\) and \(Prp_{j}\)) resulting in quick declaration of eradication, versus low-cost surveillance which requires repeat surveillance over multiple years.

The bio-economic model in Stage II identifies the surveillance effort (\(Pd_{i}\) and \(Prp_{j}\)) and time to eradication declaration that minimises costs. Because it does not optimize the \(P\left( {Erad|S^{ - } } \right)_{t}\) (sensu Regan et al. 2006), the ErrorCost t in Stage II is not the expected cost of erroneously declaring eradication success over the broadscale area of interest. The ErrorCost t in Stage II adds to the expected Stage I error costs across all MZs as a function of time to achieve the set \(P\left( {Erad|S^{ - } } \right)_{t}\). In Stage II, as the time to eradication increases, the expected costs of re-control and re-surveillance associated with erroneous declarations of MZ freedom in Stage I would be expected to increase due to the surviving population expanding in size and area (Guillera-Arroita et al. 2014; Spring et al. 2017).

The ErrorCost t for the entire area of interest in Stage II will likely vary depending on the eradication operation, but it should estimate the time-dependent re-control and re-surveillance costs not accounted for in Stage I. To illustrate, we estimated the additional expected costs due only to growth and spread of the population with increasing time until the broadscale area is declared eradicated. The total error cost across all MZs for Stage II was calculated as follows for a given number of years t to declare eradication success:

$$ErrorCost_{t} = \mathop \sum \limits_{j = 1}^{nMZ} \left( {SurveillanceCost_{j,0} \left( {1 + RecontrolFactor} \right)} \right)\left( {1 - PoF_{j} } \right)\left( {Spread_{j} } \right)$$
(11)

where \(SurveillanceCost_{j0}\) and \(RecontrolFactor\) were the same as in Stage I, \(PoF_{j}\) was the probability of freedom in MZ j in Stage I, nMZ was the total number of MZs (35), and \(Spread_{j}\) discounted the error cost for MZ j so that it estimated only the increase in control and surveillance costs due to pest-population expansion. Importantly, the Stage II \(ErrorCost_{t}\) is additive to but does not repeat the cost applied in Stage I. The bioeconomic model in Stage I would likely result in varying values of \(PoF_{j}\) across MZs; however, to simplify the simulation of Stage II, (for illustrative purposes), we used a value of 0.96 for all MZs. \(Spread_{j}\) increased with increasing years until eradication was declared:

$$Spread_{j} = years_{j} \times 0.01$$
(12)

where \(years_{j}\) ranged from 0 to 14. For example, in the first year following freedom declaration in a given MZ, Spread j would equal 0 and the additive costs of population spread would also be zero. In our Stage II error cost model (Eqs. 11, 12), ErrorCost t increases linearly each year; however non-linear models could be applied.

Results: Stage II bio-economic model

The first analysis of the potential Stage II surveillance strategies to achieve a 0.95 \(P\left( {Erad|S^{ - } } \right)\) used a high \(RecontrolFactor\) (400) to illustrate an eradication system with high financial costs of Stage I errors. Results demonstrated the total expected costs ranged more than 4.5 fold (Fig. 4a). The optimal cost-efficient strategies, as indicated by the 0.10 quantile of the total expected costs (black contour lines), were generally when the \(Pd_{i}\) was between 0.1 and 0.6 and the proportion of the SUs surveyed in a MZ were >0.2 (Fig. 4a). The corresponding optimal cost-efficient period over which to conduct surveillance ranged from 2 to 5 years after all MZs had been declared free in Stage I (Fig. 4b). Optimal surveillance effort (in the 0.1 quantile) resulted in \(P\left( {Erad|S^{ - } } \right)\) values that were equal to or just above 0.95. Values of \(P\left( {Erad|S^{ - } } \right)\) that greatly exceeded 0.95 are good probabilistically, but they required excessive effort and financial investment, and were therefore sub-optimal. Due to the discrete time periods over which surveillance occurred (i.e. years), optimal strategies appeared as ‘carved-out’ areas of the parameter space that equals or slightly exceeds 0.95 (Fig. 4). This effect is an artefact of the annual time step, which would be eliminated in practice by stopping surveillance on the month that a 0.95 \(P\left( {Erad|S^{ - } } \right)\) was achieved. The effect of increasing either re-control costs or rate of spread (Spread t ) was that optimal strategies required very high surveillance effort and achieved a 0.95 \(P\left( {Erad|S^{ - } } \right)\) within years one and two (results not displayed).

Fig. 4
figure 4

Two-dimensional images of Stage II bio-economic analysis of 10,000 potential surveillance strategies, in which the colour gradient ranges from low (blue) to high (red-brown). For each value of detection probability (\(Pd_{i}\)) and proportion SUs surveyed (\(Prp_{j}\)), the time to eradication is optimised. Using a high re-control cost (\(RecontrolFactor\) = 400), the top row of images are the optimal values for: a the relative total expected costs, and b the number of years to declare eradication. The black contour line is the 0.10 quantile of the relative total expected costs (a), indicating the range of the most cost-efficient scenarios. The second row presents results of scenarios using \(RecontrolFactor\) = 100: c the relative total expected costs, and d the number of years to declare eradication. The fragmented black contour line indicates the isolated scenarios, or small groups of scenarios are within the 0.10 quantile of expected costs

Full size image

Evaluation of the Stage II surveillance strategies that assumed a relatively low cost of wrongly declaring freedom at the MZ level (\(RecontrolFactor\) = 100) suggested that total expected costs would range more than 10-fold (Fig. 4c). Optimal cost-efficient strategies were predicted to have \(Pd_{i}\) values ranging from 0.05 to 0.60 and \(Prp_{j}\) between 0.05 and 0.9 (i.e. lowest 0.1 quantile; Fig. 4c). The corresponding optimal cost-efficient time to eradication with the low \(RecontrolFactor\) ranged from 5 to 8 years (Fig. 4d). As with the high-cost re-control scenario (above), the ‘carved out’ optimal parameter space is due to cost-efficient strategies achieving, but not greatly exceeding, the 0.95 \(P\left( {Erad|S^{ - } } \right)\) in a given year. When re-control costs or rate of spread decreased, the optimal strategies favoured low-effort surveillance that took up to 15 years to declare eradication.

Discussion

In this paper we present an analytical framework for analysing surveillance data for assessing progress and success of eradication of pests or diseases at regional or country-wide scales. The framework incorporates probability theory, ecology (and epidemiology in disease cases) of the target organism(s), and economic constraints. The formal analytical process aims to provide structure to broadscale eradication programmes so that surveillance can be used strategically in conjunction with population control to progressively advance the operation in a step-wise fashion across a broadscale area, and ultimately support a declaration of eradication success. In addition to providing an objective basis for decision-making through analysis of actual surveillance data, our proposed process will enhance the ability of managers and funders to better conceptualise an eradication problem, thereby fostering realistic and consistent expectations among managers, funders and the public. When eradication is under consideration, our approach provides the crucial evidence base for formulation of policy and for future investment in, and ongoing public and private sector support for, invasive species management activities.

Our primary intent was to describe and demonstrate the two-stage process, therefore the input parameter values in our demonstration of the two-stage bio-economic modelling were relatively arbitrary and illustrative rather than real. In addition, we modelled mean parameter values and did not incorporate uncertainty in our analysis. Clearly, a real-world application of our models would require the integration of parameter uncertainty into scenario exploration and analysis of existing surveillance data. To apply the two-stage approach to identify optimal bio-economic surveillance strategies or to analyse data from a particular broadscale operation, users would need to identify system-specific parameter distributions and apply the logic and sequence of equations described here.

The demonstration of the bio-economic optimisation process showed critical elements to incorporate and important patterns of sensitivity, which were consistent with our experience with BTB eradication from New Zealand (Gormley et al. 2016). The difference in relative costs between low- and high-cost management scenarios ranged up to 2.5 and 10 fold in Stages I and II, respectively (Figs. 3, 4). This demonstrates that over the course of a broadscale-eradication programme, surveillance data modelling has the potential to save many millions of dollars. Queensland, Australia spent $AU250 million between 2001 and 2011 in the continued eradication efforts against red imported fire ants, and it has been evaluated since that still much more work and investment will be required to achieve eradication (Keith and Spring 2013). The New Zealand BTB management programme has spent approximately $1.2 billion since 2000 (to first control, and more latterly to eradicate disease) but eradication of the infectious micro-organism that causes BTB is not projected to be achieved before 2055 (TBfree New Zealand 2015). Clearly, these are expensive operations and optimisation is required to make them economically feasible.

Applying the analytical framework described here to specific broadscale eradication programmes will require estimating detection probabilities and surveillance costs, and the costs of re-control and re-survey in the case of erroneous declarations of MZ freedom. However, general patterns emerged from our study here showing that as the cost of surveillance increases relative to error costs, the expected optimal stopping thresholds will decrease and the optimal time to declare freedom or eradication will increase (i.e. more years to eradication). In Stage I, high error costs will require high-cost surveillance to achieve a high \(P\left( {Freedom|S^{ - } } \right)\) to reduce the risk of failure at the MZ level. This is also true in Stage II, but error costs have already been accounted for in Stage I and increase only with the passage of time to eradication (Eqs. 10, 11). This is because in Stage II a surviving pest population/disease will grow and expand with time, which will increase the cost of remediation at a later date. A practical example of this happened in New Zealand in the 1980s, with the rapid spread of BTB through re-emergent possum populations when initial (1970s) vector control operations were reduced due to funding cuts (Livingstone et al. 2015).

Broadscale eradications in mainland areas are becoming an increasingly recognised strategy to enhance connectivity of threatened species to protect genetic diversity (Carroll et al. 2015), reduce the impacts of stochastic environmental events on threatened biota (McCreless et al. 2016) or to mitigate the impacts of unwanted diseases (Bellard et al. 2016; Livingstone et al. 2015). With cost being a significant factor in decisions to attempt eradication of established pests (Simberloff 2014), our two-stage analytical approach to optimise cost-efficiency could become an important tool for decision-support use in complex, multi-year eradication campaigns. The potential savings run into several millions of dollars over the course of a broadscale eradication, which demonstrates the over-riding need for bio-economic optimisation.

Supplemental material

Python computer scripts are available at the Landcare Research DataStore: http://doi.org/10.7931/J22N506H