Nonsmooth dynamic analysis of sticking impacts in rocking structures

Abstract

This paper revisits from a nonsmooth dynamics perspective the contact process encountered in two archetypal rocking structures: the rigid rocking block and the flexible rocking oscillator. The analysis assumes impact is an instantaneous (unilateral) contact, and models the behavior along the normal direction with a set-valued Newton’s law. In the tangential direction it assumes that sliding is prevented. The study formulates both impact and uplifting phenomena as linear complementarity problems (LCPs). The proposed LCP formulation encapsulates all post-impact states and liberates from the need for additional ad-hoc assumptions. The results show that the proposed nonsmooth approach verifies the corresponding results of other studies with reference to the rigid rocking block. Focusing on the flexible rocking oscillator, the proposed model is compared with pertinent analytical, numerical and experimental results from literature. The present study offers original analytical solutions describing all physically feasible post-impact states and confirms, as a special case, existing solutions of rocking initiation. Importantly, the analysis unveils that a given rocking oscillator might choose a different post-impact state (e.g. bouncing, full contact, or immediate rocking) depending on its flexural deformation at the time of impact. Further, it shows that in the case of immediate rocking after impact, the post-impact flexural velocity of the rocking oscillator is not equal with its pre-impact value. The results also reveal the dominant role of the assumed value of the Newton’s coefficient of restitution on the response-history of the rocking oscillator.

Appendix: Analytical derivation of the equations of motion

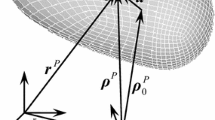
Consider a rocking oscillator (Fig. 1b) with a concentrated mass m on top, a total column mass $m_c$ uniformly distributed along its length and a rigid base with mass $m_b$. Assume the lumped mass m creates no moment of inertia, while the rigid base creates moment of inertia with respect to its center of mass equal to ${I_{{m_b}}} = {m_b}{\rho ^2}$, where $\rho$ is the radius of gyration of the base. Following Vassiliou et al. (2015), Chopra et al. (1995) the shape function that describes the deformation of the column is:

$$\begin{aligned} \psi \left( \xi \right) = \frac{{3{\xi ^2}}}{{2{h^2}}} - \frac{{{\xi ^3}}}{{2{h^3}}} \end{aligned}$$

(48)

where $\xi$ is the distance measured from the base of the column (Fig. 1b). Therefore, the deformation of the column at any arbitrary point is defined as: ${u_\xi }\left( {\xi ,t} \right) = u\left( t \right) \psi \left( \xi \right)$, where $u\left( t \right)$ denotes the generalized coordinate.

Before rocking initiates, the oscillator behaves as a generalized single degree of freedom system with generalized mass and stiffness respectively (Vassiliou et al. 2015):

$$\begin{aligned} {\tilde{m}}&= m + \int \limits _0^h {\frac{{{m_c}}}{h}{\left( {\psi \left( \xi \right) } \right) } ^2 d\xi } = m + \frac{{33}}{{140}}{m_c}\nonumber \\ {\tilde{k}}&= \int \limits _0^h {EI{{{\left( {\psi ^{\prime \prime } \left( \xi \right) } \right) }^2}}d\xi } = \frac{{3EI}}{{{h^3}}} \end{aligned}$$

(49)

After the initiation of rocking, the generalized coordinates vector for the planar rocking motion of the flexible rocking oscillator becomes: ${\mathbf{q}} = \left[ {\begin{array}{cccc} u&x&y&\phi \end{array}} \right] ^T$ (Fig. 1b). Therefore, at an arbitrary time-instant, the position of the lumped mass ($X_m$, $Y_m$), any point along the column ($X_{{m_c}}$, $Y_{{m_c}}$) and of the midpoint of the rigid base ($X_{{m_b}}$, $Y_{{m_b}}$) become respectively (Fig. 1b):

$$\begin{aligned} {X_m}&= {u_g}\left( t\right) + x - h\sin \phi + u\cos \phi \nonumber \\ {Y_m}&= y + h\cos \phi + u\sin \phi \nonumber \\ {X_{{m_c}}}&= {u_g}\left( t\right) + x - \xi \sin \phi + u\psi \cos \phi \nonumber \\ {Y_{{m_c}}}&= y + \xi \cos \phi + u\psi \sin \phi \nonumber \\ {X_{{m_b}}}&= {u_g}\left( t\right) + x \nonumber \\ {Y_{{m_b}}}&= y \end{aligned}$$

(50)

where $u_g\left( t\right)$ denotes the ground displacement measured from a reference point on the ground.

The equations of motion of the flexible rocking oscillator can be derived using the general form of the Lagrange’s equation:

$$\begin{aligned} \frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial {\dot{\phi }} }}} \right) - \frac{{\partial L}}{{\partial \phi }} = Q \end{aligned}$$

(51)

where $L = T - V$, with T the kinetic energy, V the potential energy and Q the generalized force. In particular, assuming positive (counter-clockwise) rotations, the kinetic energy of the system is:

$$\begin{aligned} T&= \frac{1}{2}m\left( \begin{array}{l} {h^2}{{\dot{\phi }}^2} + {{{\dot{u}}}^2} + {u^2}{{\dot{\phi }}^2} - 2h{\dot{u}}{\dot{\phi }} + {\dot{x}}^{2} - 2h{\dot{x}}\cos \phi {\dot{\phi }} + 2{\dot{x}}{\dot{u}}\cos \phi \\ -\, 2{\dot{x}}u\sin \phi {\dot{\phi }} + {\dot{y}}^{2} - 2h{\dot{y}}\sin \phi {\dot{\phi }} + 2{\dot{y}}{\dot{u}}\sin \phi + 2{\dot{y}}u\cos \phi {\dot{\phi }} \\ +\, {{{\dot{u}}}_g}^2 + 2{{{\dot{u}}}_g}{\dot{x}} - 2h{{{\dot{u}}}_g}\cos \phi {\dot{\phi }} + 2{{{\dot{u}}}_g}{\dot{u}}\cos \phi - 2{{{\dot{u}}}_g}u\sin \phi {\dot{\phi }} \end{array} \right) \nonumber \\&\quad +\, \frac{1}{2}{I_{{m_b}}}{{\dot{\phi }}^2} + \frac{1}{2}{m_b}\left( {{{{\dot{u}}}_g}^2 + 2{\dot{x}}{{{\dot{u}}}_g} + {\dot{x}}^{2} + {\dot{y}}^{2}} \right) \nonumber \\&\quad +\, \frac{1}{2}{m_c}\left( \begin{array}{l} \frac{{{h^2}}}{3}{{\dot{\phi }}^2} + \frac{{33}}{{140}}{{{\dot{u}}}^2} + \frac{{33}}{{140}}{u^2}{{\dot{\phi }}^2} - \frac{{11}}{{20}}h{\dot{u}}{\dot{\phi }} + {\dot{x}}^{2} - h{\dot{x}}\cos \phi {\dot{\phi }} + \frac{{3}}{{4}}{\dot{x}}{\dot{u}}\cos \phi \\ - \frac{{3}}{{4}}{\dot{x}}u\sin \phi {\dot{\phi }} + {\dot{y}}^{2} - h{\dot{y}}\sin \phi {\dot{\phi }} + \frac{{3}}{{4}}{\dot{y}}{\dot{u}}\sin \phi + \frac{{3}}{{4}}{\dot{y}}u\cos \phi {\dot{\phi }} \\ +\, {{{\dot{u}}}_g}^2 + 2{{{\dot{u}}}_g}{\dot{x}} - h{{{\dot{u}}}_g}\cos \phi {\dot{\phi }} + \frac{{3}}{{4}}{{{\dot{u}}}_g}{\dot{u}}\cos \phi - \frac{{3}}{{4}}{{{\dot{u}}}_g}u\sin \phi {\dot{\phi }} \end{array} \right) \end{aligned}$$

(52)

The potential energy due to the gravitational forces and the strain energy of the system becomes:

$$\begin{aligned} V&= \frac{1}{2} {\tilde{k}}{u^2} + mg\left( {y + h\cos \phi + u\sin \phi } \right) + {m_b}gy\nonumber \\&\quad +\, {m_c}g\left( {y + \frac{h}{2}\cos \phi + \frac{{3}}{{8}}u\sin \phi } \right) \end{aligned}$$

(53)

Finally, the work done by the non-conservative forces gives the generalized force Q:

$$\begin{aligned} {\delta } {W_{nc}} = Q{\delta } u = - 2{\zeta } \sqrt{{\tilde{m}}{\tilde{k}}} {{\dot{u}}}{\delta } u \end{aligned}$$

(54)

where $\zeta$ is the (structural) damping ratio responsible for the energy dissipation while the structure vibrates.

After substituting Eqs. (52), (53) and (54) into Eq. (51), the equations of motion of the flexible rocking oscillator become:

$$\begin{aligned} \left\{ \begin{array}{l} \left( {m + \frac{{33}}{{140}}{m_c}} \right) {\ddot{u}} + \left( {m + \frac{3}{8}{m_c}} \right) \cos \phi {\ddot{x}} + \left( {m + \frac{3}{8}{m_c}} \right) \sin \phi {\ddot{y}} - \left( {m + \frac{{11}}{{40}}{m_c}} \right) h{\ddot{\phi }} \\ =- 2\zeta \sqrt{{\tilde{m}} {\tilde{k}}} {{\dot{u}}} - {\tilde{k}}u + \left( {m + \frac{{33}}{{140}}{m_c}} \right) u{{\dot{\phi }}^2} - \left( {m + \frac{3}{8}{m_c}} \right) \cos \phi {{\ddot{u}}_g} - \left( {m + \frac{3}{8}{m_c}} \right) \sin \phi {g}\\ \\ \left( {m + \frac{3}{8}{m_c}} \right) \cos \phi {\ddot{u}} + \left( {m + {m_b} + {m_c}} \right) {\ddot{x}}\\ -\, \left( {mh\cos \phi + mu\sin \phi + \frac{1}{2}{m_c}h\cos \phi + \frac{3}{8}{m_c}u\sin \phi } \right) {\ddot{\phi }} \\= - \left( {mh\sin \phi - mu\cos \phi + \frac{1}{2}{m_c}h\sin \phi - \frac{3}{8}{m_c}u\cos \phi } \right) {{\dot{\phi }}^2}\\ +\, 2\left( {m + \frac{3}{8}{m_c}} \right) \sin \phi {\dot{u}}{\dot{\phi }} - \left( {m + {m_b} + {m_c}} \right) {{\ddot{u}}_g}\\ \\ \left( {m + \frac{3}{8}{m_c}} \right) \sin \phi {\ddot{u}} + \left( {m + {m_b} + {m_c}} \right) {\ddot{y}}\\ +\, \left( { - mh\sin \phi + mu\cos \phi - \frac{1}{2}{m_c}h\sin \phi + \frac{3}{8}{m_c}u\cos \phi } \right) {\ddot{\phi }} \\= \left( {mh\cos \phi + mu\sin \phi + \frac{1}{2}{m_c}h\cos \phi + \frac{3}{8}{m_c}u\sin \phi } \right) {{\dot{\phi }}^2}\\ -\, 2\left( {m + \frac{3}{8}{m_c}} \right) \cos \phi {{\dot{u}}}{\dot{\phi }} - \left( {m + {m_b} + {m_c}} \right) g\\ \\ -\, \left( {m + \frac{{11}}{{40}}{m_c}} \right) h{\ddot{u}} - \left( {mh\cos \phi + mu\sin \phi + \frac{1}{2}{m_c}h\cos \phi + \frac{3}{8}{m_c}u\sin \phi } \right) {\ddot{x}}\\ +\, \left( { - mh\sin \phi + mu\cos \phi - \frac{1}{2}{m_c}h\sin \phi + \frac{3}{8}{m_c}u\cos \phi } \right) {\ddot{y}}\\ +\, \left( {{I_{{m_b}}} + m{h^2} + \frac{1}{3}{m_c}{h^2} +\left( m + \frac{{33}}{{140}}{m_c}\right) {u^2}} \right) {\ddot{\phi }} \\= - 2\left( {m + \frac{{33}}{{140}}{m_c}} \right) u{{\dot{u}}}{\dot{\phi }} + \left( {mh\cos \phi + mu\sin \phi + \frac{1}{2}{m_c}h\cos \phi + \frac{3}{8}{m_c}u\sin \phi } \right) {{\ddot{u}}_g}\\ -\, g\left( { - mh\sin \phi + mu\cos \phi - \frac{1}{2}{m_c}h\sin \phi + \frac{3}{8}{m_c}u\cos \phi } \right) \end{array} \right. \end{aligned}$$

(55)