Spatio-temporal stiffness optimization with switching dynamics

Abstract

We address the optimal control problem of robotic systems with variable stiffness actuation (VSA) including switching dynamics and discontinuous state transitions. Our focus in this paper is to consider dynamic tasks that have multiple phases of movement, contacts and impacts with the environment with a requirement of exploiting passive dynamics of the system. By modelling such tasks as a hybrid dynamical system with time-based switching, we develop a systematic methodology to simultaneously optimize control commands, time-varying stiffness profiles and temporal aspect of the movement such as switching instances and total movement duration to exploit the benefits of VSA. Numerical evaluations on a brachiating robot driven with VSA and a hopping robot equipped with variable stiffness springs demonstrate the effectiveness of the proposed approach. Furthermore, hardware experiments on a two-link brachiating robot with VSA highlight the applicability of the proposed framework in a challenging task of brachiation.

Introduction

Towards the aim of achieving highly dynamic and flexible movements in close interaction with the environment, a number of variable stiffness actuators (VSAs) have been recently developed (Van Ham et al. 2007; Catalano et al. 2010; Hurst et al. 2010; Eiberger et al. 2010; Jafari et al. 2010) (see (Van Ham et al. 2009) for reviews). VSAs are composed of mechanically adjustable compliant (passive) mechanisms with the capability of simultaneous modulation of stiffness and output torque. In contrast to conventional stiff actuators, VSAs are expected to have desirable properties such as intrinsic compliance, energy storage capability with potential applications in human-robot interaction and improvements of task performance in dynamic tasks.

Despite potential benefits of variable stiffness joints, finding an appropriate control strategy to fully exploit the capabilities of VSAs is challenging due to the increased complexity of mechanical properties and the number of control variables (redundancy in actuation). Taking an optimal control approach, recent studies have investigated the benefits of VSA such as energy storage in explosive movements from a viewpoint of performance improvement (Braun et al. 2012, 2013; Garabini et al. 2011; Haddadin et al. 2011). Such benefits of VSAs in a ball throwing task has been demonstrated by simultaneously optimizing time-varying torque and stiffness profiles of the actuator (Braun et al. 2012) with a focus on an optimal control formulation under actuation constraints for complex hardware mechanisms in VSAs (Braun et al. 2013). An optimal control problem of maximizing link velocity with VSA models has been investigated by Garabini et al. (2011) and Haddadin et al. (2011). It is shown that much larger link velocity can be achieved than that of the motor in the VSA with the help of appropriate stiffness adjustment during a hitting movement. In a similar problem, Hondo and Mizuuchi (2011) have discussed the issue of determining the inertia parameter and spring constant in the design of series elastic actuators to increase peak velocity. In robot running, Karssen and Wisse (2011) have presented numerical studies to demonstrate that an optimized nonlinear leg stiffness profile could improve robustness against disturbances.

However, traditional approaches have focused on the optimal control formulation over a predetermined time horizon with smooth, continuous plant dynamics. When considering tasks that consist of multiple phases of movements including switching dynamics and discrete state transition (arising from interaction with the environment), an individual phase-by-phase optimization strategy could result in a suboptimal solution.

In this paper, we investigate spatio-temporal stiffness optimization in such problems in order to exploit the benefits of VSA. In addition to optimizing control commands and stiffness, we develop a systematic methdology to simultaneously optimize the temporal aspect of the movement (e.g., movement duration). We address optimization problems for tasks with multi-phase movements including switching dynamics, impacts and contacts with environments in tasks requiring exploitation of intrinsic dynamics in underactuated systems.

In order to demonstrate the effectiveness of the proposed approach, we present numerical evaluations of robot brachiation and hopping driven by VSA. In addition, we report hardware implementation of the proposed approach on a physical two-link brachiating robot with VSA to demonstrate its applicability in achieving highly dynamic movements under real-world conditions.

Spatio-temporal optimization of multi-phase movements

Dynamics with intermittent contacts and impacts such as locomotion and juggling are often modelled as hybrid dynamical systems which consist of (multiple sets of switching) continuous dynamics and discontinuous state transition determined by switching surfaces (state based switching) (Bätz et al. 2010; Grizzle et al. 2001; Rosa et al. 2012; Long et al. 2011). From a control theoretic perspective, a significant effort has been made to address optimal control problems of various class of hybrid systems (Branicky et al. 1998; Sussmann 1999; Xu and Antsaklis 2003, 2004). However, illustrative examples in the control literature are confined to low-dimensional and simple dynamical systems, and only a few robotic applications can be found for optimization of movements over multiple phases (Buss et al. 2002; Long et al. 2011). Instead of using hybrid dynamics modelling, different optimization approaches to dealing with multiple contact events have been proposed. Tassa et al. (2012) have proposed an iLQG (iterative linear quadratic Gaussian)-based (Li and Todorov 2007) model based predictive control with smooth approximation of contact forces for online motion synthesis of a simulated humanoid model without the need of switching dynamics. A direct trajectory optimization method for rigid body systems subject to collisions by sequential quadratic programming has been proposed (Posa et al. 2014). In the study by Posa et al. (2014), contact forces are explicitly included as constraint forces with complementarity conditions and directly optimized together with trajectories and control commands.

Solving hybrid optimal control problems with state based switching is non-trivial even if the number and the sequence of switching are known a priori. One of the reasons is that additional constraints need to be satisfied such that the states must lie on the switching surface at the instance of switching. Furthermore, it is necessary to find the time of the switching instance influenced by the control commands, whose analytical expression is difficult to obtain in general (Xu and Antsaklis 2004). These conditions are equivalent to having several interior-point constraints forming a multipoint boundary value problem, which is generally known to be hard to find solutions (Bryson and Ho 1975).

Thus, we suggest an approximate approach to the hybrid optimal control problem, where the multiple phases of movement are modelled as time-based switching hybrid dynamics assuming that the sequence of switching is known. Necessary conditions for optimality in the case of time-based switching is simpler than those of state-based switching (Xu and Antsaklis 2004) and can be dealt with based on the optimization method we use in this paper.

The main ingredients of the proposed optimal control framework in this paper are as follows:

• 1. use of nonlinear time-based switching dynamics with continuous control input to model the dynamics of multi-phase movements;

• 2. use of nonlinear discrete state transition to model contacts and impacts;

• 3. use of realistic plant dynamics with a VSA model;

• 4. introduction of a composite cost function to describe task objectives with multi-phase movements;

• 5. simultaneous optimization of joint torque and stiffness profiles across multiple phases;

• 6. optimization of switching instances and total movement duration.

We formulate this problem as an extension of an iterative linear quadratic regulator (iLQR) algorithm (Li and Todorov 2007) and generalization of switched LQ control with state jumps (Xu and Antsaklis 2003). iLQR is an effective method for iteratively solving optimal control problems and has been employed in our previous work, e.g, by Braun et al. (2012, 2013). To our knowledge, while there exists previous work separately addressing some of the specific points above (Xu and Antsaklis 2003, 2004; Egerstedt et al. 2003; Caldwell and Murphey 2012), we have yet to find a study which has considered all these issues in conjunction. In addition, the proposed formulation provides an optimal feedback control law, while many trajectory optimization algorithms typically compute only optimal feedforward controls. Discussions on alternative optimal control approaches such as indirect methods and direct methods can be found in (Braun et al. 2013).

Problem formulation

We present a general formulation of optimal control problems for tasks with multiple phase movements including switching dynamics and discrete state transition arising from interactions with an environment.

Robot dynamics with variable stiffness actuation

To describe multi-phase movements, we consider multiple sets of robot dynamics. An individual rigid body dynamics model is defined for each associated phase of the movement as a subsystem. The servo motor dynamics in the VSA is modelled as a critically damped second order dynamical system:

$$\begin{aligned}&\mathbf{M}_i(\mathbf{q})\ddot{\mathbf{q}} + \mathbf{C}_i(\mathbf{q},\dot{\mathbf{q}})\dot{\mathbf{q}} + \mathbf{g}_i(\mathbf{q}) + \mathbf{D}_i \dot{\mathbf{q}}=\varvec{\tau }_i(\mathbf{q},\mathbf{q}_m) \end{aligned}$$

(1)

$$\begin{aligned}&\ddot{\mathbf{q}}_m + 2 \varvec{\alpha }_i \dot{\mathbf{q}}_m+ \varvec{\alpha }_i^2 \mathbf{q}_m = \varvec{\alpha }_i^2 \mathbf{u}\end{aligned}$$

(2)

where i denotes the ith subsystem, $\mathbf{q}\in \mathbb {R}^n$ is the joint angle vector, $\mathbf{q}_m \in \mathbb {R}^m$ is the motor position vector of the VSA, $\mathbf{M}_i \in \mathbb {R}^{n \times n}$ is the inertia matrix, $\mathbf{C}_i \in \mathbb {R}^n$ is the Coriolis term, $\mathbf{g}_i \in \mathbb {R}^n$ is the gravity vector, $\mathbf{D}_i \in \mathbb {R}^{n \times n}$ is the viscous damping matrix, and $\varvec{\tau }\in \mathbb {R}^n$ are the joint torques from the variable stiffness mechanism. In the equations above, (1) denotes the rigid body dynamics of the robot and (2) denotes the servo motor dynamics in the VSA. In (2), $\varvec{\alpha }$ determines the bandwidth of the servo motors¹ and $\mathbf{u}\in \mathbb {R}^m$ is the motor position command (Braun et al. 2012). We assume that the range of the control command $\mathbf{u}$ is limited as $\mathbf{u}_{ min } \preceq \mathbf{u}\preceq \mathbf{u}_{ max }$. Note that since the motor dynamics (2) are critically damped, the range constraint on the servo motor positions $\mathbf{u}_{ min } \preceq \mathbf{q}_m \preceq \mathbf{u}_{ max }$ can also be imposed² (Braun et al. 2012).

In this paper, we consider a VSA model in which the joint torques are given in the form

$$\begin{aligned} \varvec{\tau }(\mathbf{q}, \mathbf{q}_m) = \mathbf{A}^T(\mathbf{q}, \mathbf{q}_m) \mathbf{F}(\mathbf{q}, \mathbf{q}_m) \end{aligned}$$

(3)

where $\mathbf{A}$ is the moment arm matrix and $\mathbf{F}$ is the forces generated by the elastic elements. The joint stiffness is defined as

$$\begin{aligned} \mathbf{K}(\mathbf{q}, \mathbf{q}_m) = -\frac{\partial \varvec{\tau }(\mathbf{q},\mathbf{q}_m)}{\partial \mathbf{q}}. \end{aligned}$$

(4)

State space representation

In order to formulate an optimal control problem, we consider the following state space representation of the combined plant dynamics composed of the rigid body dynamics (1) and the servo motor dynamics (2):

$$\begin{aligned} \dot{\mathbf{x}}= \mathbf{f}_i(\mathbf{x}, \mathbf{u}) \end{aligned}$$

(5)

where

$$\begin{aligned} \mathbf{f}_i=\left[ \begin{array}{c} \mathbf{x}_2\\ \mathbf{M}_i^{-1}(\mathbf{x}_1) \left( -\mathbf{C}_i (\mathbf{x}_1,\mathbf{x}_2)\mathbf{x}_2 - \mathbf{g}_i (\mathbf{x}_1) - \mathbf{D}_i \mathbf{x}_2 + \varvec{\tau }_i(\mathbf{x}_1,\mathbf{x}_3) \right) \\ \mathbf{x}_4 \\ -\varvec{\alpha }_i^2 \mathbf{x}_3 -2 \varvec{\alpha }_i\mathbf{x}_4+\varvec{\alpha }_i^2 \mathbf{u}\\ \end{array} \right] \nonumber \\ \end{aligned}$$

(6)

and $\mathbf{x}= [\;\mathbf{x}_1^T,\;\mathbf{x}_2^T,\;\mathbf{x}_3^T,\;\mathbf{x}_4^T\;]^T = [\;\mathbf{q}^T,\;\dot{\mathbf{q}}^T,\;\mathbf{q}_m^T,\;\dot{\mathbf{q}}_m^T\;]^T \in \mathbb {R}^{2(n+m)}$ is the state vector consisting of the robot state and the servo motor state. For more detailed treatment of modelling robot dynamics with compliantly actuated systems, please refer to (Braun et al. 2013).

Fig. 1

A hybrid system with time-based switching dynamics and discrete state transition with a known sequence. The objective is to find an optimal control command $\mathbf{u}$, switching instances $T_i$ and final time $T_f$ which minimizes the composite cost $J= J_1+ \cdots + J_{K+1}$

Hybrid dynamics with time-based switching and discrete state transition

In this paper, we employ a hybrid dynamics representation to model multi-phase movements having interactions with an environment. Hybrid dynamical systems consist of (multiple sets of) switching continuous dynamics and discrete state transition (Xu and Antsaklis 2004) and have been widely used to model robot dynamics with impacts and contacts (Bätz et al. 2010; Grizzle et al. 2001; Rosa et al. 2012; Long et al. 2011). In these physical systems, switching or discrete state transition occurs based on the state of the system, e.g., foot contact in the case of locomotion. However, as mentioned in Sect. 1.1, optimal control of state based switching hybrid dynamics is non-trivial due to difficulty in dealing with transversality conditions arising from multiple interior-point constraints. Thus, we consider the following class of hybrid systems with time-based switching to represent the movement with multiple phases (Xu and Antsaklis 2004; Caldwell and Murphey 2012):

$$\begin{aligned} \dot{\mathbf{x}}= & {} \mathbf{f}_{i_j}(\mathbf{x}, \mathbf{u}),\quad T_j \le t < T_{j+1} \end{aligned}$$

(7)

$$\begin{aligned} \mathbf{x}\left( T_j^+\right)= & {} \varvec{\Delta }^{i_{j-1},i_j} \left( \mathbf{x}\left( T_j^-\right) \right) \end{aligned}$$

(8)

where $\mathbf{f}_{i_j}: \mathbb {R}^n \times \mathbb {R}^m \rightarrow \mathbb {R}^n$ is the subsystem $i_j$, $\mathbf{x}\in \mathbb {R}^{n}$ is a state vector and $\mathbf{u}\in \mathbb {R}^{m}$ is a control input vector for subsystems. For $T_j \le t < T_{j+1}$, the subsystem $i_j$ is active and at $t=T_j$, the subsystem switches from $i_{j-1}$ to $i_j$. At the moment of dynamics switching, we assume an instantaneous discrete (discontinuous) state transition, which is denoted by a map $\varvec{\Delta }^{i_{j-1},i_j}$ in (8), where $\mathbf{x}(T_j^+)$ and $\mathbf{x}(T_j^-)$ denote the post- and pre-transition states, respectively. The indices are defined as $j=0,\ldots ,K$ for (7) and $j=1,\ldots ,K$ for (8), respectively.

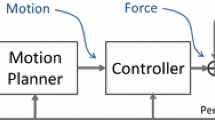
An example of an instantaneous state transition is an impact map arising from an inelastic collision of the rigid body with an environment (Grizzle et al. 2001; Rosa et al. 2012; Bätz et al. 2010). In the proposed framework, equality constraints at the moment of switching will be approximately imposed by the via-point cost and appropriate time for the event will be found by optimizing switching instances as we discuss below. In this paper, the sequence of switching is assumed to be given. Figure 1 depicts a schematic diagram of a hybrid system we consider in this paper.

Movement optimization of multiple phases

For the given hybrid dynamics (7) and (8), in order to describe the full movement with multiple phases, we consider the following composite cost function

$$\begin{aligned} J=\phi (\mathbf{x}(T_f)) + \sum _{j=1}^K \psi ^j\left( \mathbf{x}\left( T_j^-\right) \right) + \int _{T_0}^{T_f} h(\mathbf{x}, \mathbf{u}) dt \end{aligned}$$

(9)

where $\phi (\mathbf{x}(T_f))$ is the terminal cost, $\psi ^j(\mathbf{x}(T_j^-))$ is the via-point cost at the jth switching instance and $h(\mathbf{x}, \mathbf{u})$ is the running cost.

In our earlier work (Nakanishi and Vijayakumar 2012), we attempted to obtain multiple sequence of swing locomotion in a robot brachiation example by optimizing each cost function $J_i$ for each phase separately in a sequential manner, where

$$\begin{aligned} J_j = \psi ^j\left( \mathbf{x}\left( T_j^-\right) \right) + \int _{T_{j-1}}^{T_j} h(\mathbf{x}, \mathbf{u}) dt\quad \text {for } j=1, \ldots , K\nonumber \\ \end{aligned}$$

(10)

and

$$\begin{aligned} J_{K+1} = \phi (\mathbf{x}(T_f)) + \int _{T_K}^{T_f} h(\mathbf{x}, \mathbf{u}) dt \end{aligned}$$

(11)

using the terminal state for the jth sequence as the initial condition for the $(j+1)$-st sequence with the discrete state transition (8). In this case, each cost function can be (locally) optimized. However, the total cost $J = \sum _{j=1}^{K+1} J_j$ may be suboptimal.

For the given plant dynamics (7) and state transition (8), the optimization problem we consider is to a) find an optimal feedback control law $\mathbf{u}= \mathbf{u}(\mathbf{x}, t)$ which minimizes the composite cost (9) and b) simultaneously optimize switching instances $T_1, \ldots , T_k$ and the final time $T_f$ as well.

Spatio-temporal optimization algorithm for timed switching dynamics and discontinuous state transitions

In this section, first we extend iLQR—an approximate local optimal feedback control solver (similar arguments apply for the stochastic equivalent iLQG (Li and Todorov 2007)) with generalization of the switched LQ control with state jumps (Xu and Antsaklis 2003) in order to incorporate timed switching nonlinear dynamics with discrete and discontinuous state transitions. Then, we present a temporal optimization algorithm to optimize the switching instances and the total movement duration. Note that traditional single phase movement optimization can be simply treated as a single set of continuous time dynamics without switching and discontinuous state transition.

Optimal control of switching dynamics and discrete state transition

In brief, the iLQR method solves an optimal control problem of the locally linear quadratic approximation of the nonlinear dynamics and the cost function around a nominal trajectory $\bar{\mathbf{x}}$ and control sequence $\bar{\mathbf{u}}$ in discrete time, and iteratively improves the solutions.

In order to incorporate switching dynamics and discrete state transition, the hybrid dynamics (7) and (8) are linearized in discrete time around the nominal trajectory and control sequence as

$$\begin{aligned} \delta \mathbf{x}_{k+1}= & {} \mathbf{A}_k \delta \mathbf{x}_k + \mathbf{B}_k \delta \mathbf{u}_k \end{aligned}$$

(12)

$$\begin{aligned} \delta \mathbf{x}_{k_j}^{+}= & {} \varvec{\Gamma }_{k_j} \delta \mathbf{x}_{k_j}^{-} \end{aligned}$$

(13)

$$\begin{aligned} \mathbf{A}_k= & {} \mathbf{I}+ \Delta t_j \textstyle { \left. \frac{\partial \mathbf{f}_{i_j}}{\partial \mathbf{x}} \right| _{\mathbf{x}=\mathbf{x}_k}},\quad \mathbf{B}_k=\Delta t_j\textstyle {\left. \frac{\partial \mathbf{f}_{i_j}}{\partial \mathbf{u}} \right| _{\mathbf{u}=\mathbf{u}_k}} \end{aligned}$$

(14)

$$\begin{aligned} \varvec{\Gamma }_{k_j}= & {} \textstyle {\left. \frac{\partial \varvec{\Delta }^{i_{j-1},i_j}}{\partial \mathbf{x}} \right| _{\mathbf{x}=\mathbf{x}_{k_j}^{-}}} \end{aligned}$$

(15)

where $\delta \mathbf{x}_k = \mathbf{x}_k - \bar{\mathbf{x}}_k$, $\delta \mathbf{u}_k = \mathbf{u}_k - \bar{\mathbf{u}}_k$, k is the discrete time step, $\Delta t_j$ is the sampling time for the time interval $T_j \le t < T_{j+1}$, and $k_j$ is the jth switching instance in the discretized time step. The sampling time $\Delta t_j$ will be optimized for the purpose of temporal optimization as described in Sect. 3.2.

The composite cost function (9) is locally approximated in a quadratic form as³

$$\begin{aligned} \Delta J= & {} \delta \mathbf{x}_N^T \phi _{\mathbf{x}} + \frac{1}{2} \delta \mathbf{x}_N^T \phi _{\mathbf{x}\mathbf{x}} \delta \mathbf{x}_N \nonumber \\&+\sum _{j=1}^K \left( \left( \delta \mathbf{x}_{k_j}^-\right) ^T \psi ^j_{\mathbf{x}} + \frac{1}{2} \left( \delta \mathbf{x}_{k_j}^{-}\right) ^{T} \psi ^j_{\mathbf{x}\mathbf{x}} \delta \mathbf{x}_{k_j^-} \right) \nonumber \\&+\sum _{k=1}^N \left( \delta \mathbf{x}_k^T h_{\mathbf{x}} + \delta \mathbf{u}_k^T h_{\mathbf{u}} + \frac{1}{2} \delta \mathbf{x}_k^T h_{\mathbf{x}\mathbf{x}} \delta \mathbf{x}_k \right. \nonumber \\&+\left. \frac{1}{2} \delta \mathbf{u}_k^T h_{\mathbf{u}\mathbf{u}} \delta \mathbf{u}_k + \delta \mathbf{u}_k^T h_{\mathbf{u}\mathbf{x}} \delta \mathbf{x}_k \right) \Delta t_j \end{aligned}$$

(16)

and a local quadratic approximation of the optimal cost-to-go function is defined as

$$\begin{aligned} v_k(\delta \mathbf{x}_k) = \frac{1}{2} \delta \mathbf{x}_k^T \mathbf{S}_k \delta \mathbf{x}_k + \delta \mathbf{x}_k^T \mathbf{s}_k. \end{aligned}$$

(17)

The local control law $\delta \mathbf{u}_k$ of the form

$$\begin{aligned} \delta \mathbf{u}_k = \mathbf{l}_k + \mathbf{L}_k \delta \mathbf{x}_k \end{aligned}$$

(18)

is obtained from the Bellman equation

$$\begin{aligned} v_k(\delta \mathbf{x}_k) = \min _{\delta \mathbf{u}} \{ h_k(\delta \mathbf{x}_k,\delta \mathbf{u}_k) + v_{k+1}(\delta \mathbf{x}_{k+1}) \} \end{aligned}$$

(19)

by substituting (12) and (17) into the Eq.(19), where $h_k$ is the local approximation of the running cost in (16) (see Li and Todorov 2007 for details).

For the dynamics (12), the cost-to-go parameters $\mathbf{S}_k$, $\mathbf{s}_k$ in (17) are updated with a modified Riccati equation⁴

$$\begin{aligned} \mathbf{S}_k= & {} h_{\mathbf{x}\mathbf{x}} + \mathbf{A}_k^T \mathbf{S}_{k+1} \mathbf{A}_k + \mathbf{L}_k^T \mathbf{H}\mathbf{L}_k + \mathbf{L}_k^T \mathbf{G}+ \mathbf{G}^T \mathbf{L}_k \end{aligned}$$

(20)

$$\begin{aligned} \mathbf{s}_k= & {} h_{\mathbf{x}} + \mathbf{A}_k^T \mathbf{s}_{k+1} + \mathbf{L}_k^T \mathbf{H}\mathbf{l}_k + \mathbf{L}_k^T \mathbf{g}+ \mathbf{G}^T \mathbf{l}_k \end{aligned}$$

(21)

where

$$\begin{aligned} \mathbf{H}= & {} h_{\mathbf{u}\mathbf{u}} + \mathbf{B}_k^T \mathbf{S}_{k+1} \mathbf{B}_k \end{aligned}$$

(22)

$$\begin{aligned} \mathbf{G}= & {} h_{\mathbf{u}\mathbf{x}} + \mathbf{B}_k^T \mathbf{S}_{k+1} \mathbf{A}_k \end{aligned}$$

(23)

$$\begin{aligned} \mathbf{g}= & {} h_{\mathbf{u}} + \mathbf{B}_k^T \mathbf{s}_{k+1} . \end{aligned}$$

(24)

At the instance of discrete state transition $k=k_j$, the following cost-to-go parameter update is added (cf. Xu and Antsaklis 2003):

$$\begin{aligned} \mathbf{S}_{k_j}^{-}= & {} \psi ^j_{\mathbf{x}\mathbf{x}} + \varvec{\Gamma }_{k_j}^T \mathbf{S}_{k_j}^{+} \varvec{\Gamma }_{k_j} \end{aligned}$$

(25)

$$\begin{aligned} \mathbf{s}_{k_j}^{-}= & {} \psi ^j_{\mathbf{x}} + \varvec{\Gamma }_{k_j}^T \mathbf{s}_{k_j}^{+} \end{aligned}$$

(26)

which is derived from the Bellman equation

$$\begin{aligned} v_{k_j}(\delta \mathbf{x}_{k_j}^{-}) = \psi _{k_j}^j (\delta \mathbf{x}_{k_j}^-) + v_{k_j}(\delta \mathbf{x}_{k_j}^{+}) \end{aligned}$$

(27)

at $k=k_j$, where $\psi _{k_j}^j (\delta \mathbf{x}_{k_j}^-)$ is the local approximation of the via-point cost (16).

Once we have a locally optimal control command $\delta \mathbf{u}$, the nominal control sequence is updated as $\bar{\mathbf{u}} \leftarrow \bar{\mathbf{u}} + \delta \mathbf{u}$. Then, the new nominal trajectory $\bar{\mathbf{x}}$ is computed by running the obtained control $\bar{\mathbf{u}}$ and the above process is iterated until convergence (no further improvement in the cost within certain threshold). In (Tassa et al. 2012), methods for improving convergence and robustness properties of the iLQR/iLQG algorithms are presented in the context of online trajectory optimization.

Temporal optimization

In our prior work, a temporal optimization algorithm has been proposed to simultaneously optimize the control commands and temporal parameters (Rawlik et al. 2010). A mapping $\beta (t)$ from the real time t to a canonical time $t'$ is introduced as

$$\begin{aligned} t' = \int _0^t \frac{1}{\beta (s)} ds, \end{aligned}$$

(28)

and then $\beta (t)$ is optimized to scale the temporal aspect of the movement. In the case of single phase movement optimization, (28) can be discretized with an assumption that $\beta (t)$ and $\Delta t$ are constant throughout the movement as $\Delta t' = \frac{1}{\beta } \Delta t$.

In order to optimize the switching instances and the total movement duration, we introduce a scaling parameter and sampling time for each duration between switching as (cf. (14), (16))

$$\begin{aligned} \Delta t_j' = \frac{1}{\beta _j} \Delta t_j\quad \text { for } \quad T_j \le t < T_{j+1} \end{aligned}$$

(29)

where $j=0, \ldots , K$. By optimizing the vector of temporal scaling factors $\varvec{\beta }= [\;\beta _0,\;\ldots ,\;\beta _K\;]^T$ via gradient descent

$$\begin{aligned} \varvec{\beta }\leftarrow \varvec{\beta }- \eta \nabla _{\beta } J \end{aligned}$$

(30)

where $\eta >0$ is a learning rate, we can obtain each switching instance

$$\begin{aligned} T_{j+1} = (k_{j+1}-k_j) \Delta t_j' + T_j \end{aligned}$$

(31)

and total movement duration

$$\begin{aligned} T_f = \sum _{j=0}^K (k_{j+1}-k_j) \Delta t_j' + T_0 \end{aligned}$$

(32)

where $k_0=1$ and $k_{K+1} = N$. In the complete optimization, computation of optimal feedback control law and temporal scaling parameter update are iteratively performed until convergence. A pseudocode of the complete algorithm is summarized in Algorithm 1.

This iterative temporal optimization algorithm with alternative update of control commands and temporal parameters has been proposed in the general context of an inference based stochastic optimal control framework in (Rawlik et al. 2010; Rawlik 2013). As discussed in (Rawlik 2013), because it is generally intractable to obtain the combined optimal policy at once, the idea of the two step procedure has been introduced. In each iteration, improvement of control commands and temporal parameters will be performed to jointly reduce the cost function. In addition, in the control theoretic literature, a similar iterative two stage strategy has been proposed for a class of switching systems to optimize control commands and switching instances (Xu and Antsaklis 2004).

As a result of these iterative optimization procedures, at best, convergence to a locally optimal solution could be expected. Effectiveness of this approach has been illustrated in variable distance and via-point reaching tasks (Rawlik et al. 2010; Rawlik 2013) and in simple numerical examples of a class of switching systems (Xu and Antsaklis 2004).

Exploitation of passive dynamics with spatio-temporal optimization of stiffness

We explore the benefit of simultaneous variable stiffness and temporal optimization for tasks exploiting intrinsic dynamics of the system. We consider brachiation (Saito et al. 1994; Nakanishi et al. 2000; Gomes and Ruina 2005; Rosa et al. 2012) as an example of highly dynamic maneuver requiring utilization of passive dynamics for successful task execution.

Brachiating robot dynamics with VSA

The equation of motion of the two-link brachiating robot shown in Fig. 2 (See Sect. 5.3 for the description of the hardware platform) takes the standard form of rigid body dynamics where only the second joint has actuation:

$$\begin{aligned} \mathbf{M}(\mathbf{q}) \ddot{\mathbf{q}} + \mathbf{C}(\mathbf{q}, \dot{\mathbf{q}})\dot{\mathbf{q}} + \mathbf{g}(\mathbf{q}) + \mathbf{D}\dot{\mathbf{q}} = \left[ \begin{array}{c} 0\\ \tau (\mathbf{q}, \mathbf{q}_m)\\ \end{array} \right] \end{aligned}$$

(33)

where $\mathbf{q}= [\;q_1,\;q_2\;]^T$ is the joint angle vector, $\mathbf{M}$ is the inertia matrix, $\mathbf{C}$ is the Coriolis term, $\mathbf{g}$ is the gravity vector, $\mathbf{D}$ is the viscous damping matrix, $\tau$ is the joint torque acting on the second joint given by the VSA, and $\mathbf{q}_m$ is the motor positions in the VSA as described below.

Fig. 2

Two-link brachiating robot model with the VSA joint with the inertial and geometric parameters. See Sect. 5.3 for the description of the hardware platform. The parameters of the robot are given in Table 1. Note that the indices i denote the link number in this figure and Table 1

We use MACCEPA (Van Ham et al. 2007) as our VSA implementation of choice. MACCEPA is one of the designs of mechanically adjustable compliant actuators with a passive elastic element (cf. Fig. 2). This actuator design has the desirable characteristics that the joint can be very passively compliant. This allows free swinging with a large range of movement by relaxing the spring. Thus, it is highly suitable for the brachiation task we consider. MACCEPA is equipped with two position controlled servo motors, $\mathbf{q}_m=[\;q_{m1},\;q_{m2}\;]^T$, which control the equilibrium position and the spring pre-tension, respectively.

The joint torque for this actuator model is given by

$$\begin{aligned} \tau = \frac{BC \sin (q_{m1} - q)}{\gamma }\,F \end{aligned}$$

(34)

where $\gamma = \sqrt{B^2 + C^2-2 B C \cos \left( q_{m1}-q\right) }$, q is the joint angle⁵, F is the spring tension,

$$\begin{aligned} F = \kappa (l-l_0) \end{aligned}$$

(35)

$\kappa$ is the spring constant, $l = \gamma + r_d q_{m2}$ is the current spring length, $l_0 = C-B$ is the spring length at rest and $r_d$ is the drum radius (see Fig. 2 for the definition of the model parameters). The joint stiffness can be computed as

$$\begin{aligned} k = -\frac{\partial \tau }{\partial q}. \end{aligned}$$

(36)

Note that MACCEPA has a relatively simple configuration in terms of actuator design compared to other VSAs, however, the torque and stiffness relationships in (34) and (36) are dependent on the current joint angle and two servo motor angles in a complicated manner and its control is not straightforward.

In addition, we include position controlled servo motor dynamics approximated by a second order system with a PD feedback control (Braun et al. 2012)

$$\begin{aligned} \ddot{\mathbf{q}}_{m} + 2 \varvec{\alpha }\dot{\mathbf{q}}_{m} +\varvec{\alpha }^2 \mathbf{q}_{m} = \varvec{\alpha }^2 \mathbf{u}\end{aligned}$$

(37)

where $\mathbf{u}=[\;u_1,\;u_2\;]^T$ is the motor position command, $\varvec{\alpha }$ determines the bandwidth of the actuator. In this study, we use $\varvec{\alpha }=\mathrm {diag}(20, 25)$. The range of the commands of the servo motors are limited as $u_1 \in [-\pi /2, \pi /2]$ and $u_2 \in [0, \pi /2]$.

We use the model parameters of the hardware platform (see Sect. 5.3 for details) shown in Table 1 and the MACCEPA parameters with the spring constant $\kappa = 771$ N/m, the lever length $B = 0.03$ m, the pin displacement $C=0.125$ m and the drum radius $r_d = 0.01$ m.

Table 1 Model parameters of the two-link brachiating robot

Optimization of single phase movement in brachiation task

A natural and desirable strategy for a swing movement in brachiation would be to make good use of gravity by making the joints passive and compliant. For a system with VSAs, our idea in exploiting passive dynamics is to frame the control problem in finding an appropriate (preferably small) stiffness profile to modulate the system dynamics only when necessary and compute the virtual equilibrium trajectory (Shadmehr 1990) to fulfill the specified task requirement.

To implement this idea of passive control strategy, we consider the following cost function to encode the task (the specific reason will be explained below)

$$\begin{aligned}&J=(\mathbf{y}(T) - \mathbf{y}^*)^T \mathbf{Q}_T (\mathbf{y}(T) - \mathbf{y}^*) \nonumber \\&\quad +\int _{0}^T \left( \mathbf{u}^T \mathbf{R}_1 \mathbf{u}+ R_2 F^2 \right) dt \end{aligned}$$

(38)

where $\mathbf{y}= [\;\mathbf{r},\;\dot{\mathbf{r}}\;]^T \in \mathbb {R}^4$ is the position and the velocity of the gripper in the Cartesian coordinates, $\mathbf{y}^*$ is the target value when reaching the target $\mathbf{y}^* = [\;\mathbf{r}^*,\;\mathbf{0}\;]^T$ and F is the spring tension in the VSA. This objective function is designed in order to reach the target located at $\mathbf{r}^*$ at the specified time T while minimizing the spring tension F in the VSA. Note that the main component in the running cost is to minimize the spring tension F by the second term while the first term $\mathbf{u}^T \mathbf{R}_1 \mathbf{u}$ is added for regularization with a small choice of the weights in $\mathbf{R}_1$. In practice, this is necessary since F is a function of the state and iLQR requires a control cost in its formulation to compute the optimal control law.

Notice that the actuator torque (34) can be expressed in the form

$$\begin{aligned} \tau = - F \sin (q - q_{m1})/\gamma ' \end{aligned}$$

(39)

where $\gamma ' = \gamma / BC$. In this Eq. (39), it can be conceived that F has a similar role to the stiffness parameter k as in the simplified actuator model $\tau = -k(q-q_m)$. Another interpretation can be considered in such a way that if we linearize (34) around the equilibrium position assuming that $q_{m1}-q \ll 1$, the relationship between the joint stiffness k in (36) and the spring tension F can be approximated as

$$\begin{aligned} k \approx \frac{1}{\sqrt{B^2+C^2-2BC}} F. \end{aligned}$$

(40)

Thus, effectively, minimizing the spring tension F corresponds to minimizing the stiffness k in an approximated way. Note that it is possible to directly use k in the cost function. However, in practice, first and second derivatives of k are needed to implement the iLQG algorithm which become significantly more complex than those of F.

Benefit of temporal optimization

This section numerically explores the benefit of temporal optimization in exploiting natural dynamics of the system. One of the issues in a conventional optimal control formulation is that the time horizon needs to be given in advance for a given task. While on fully actuated systems, control can be used to enforce a pre-specified timing, it is not possible to choose an arbitrary time horizon on underactuated systems. In a brachiation task, determination of an appropriate movement horizon, i.e., matching the movement duration corresponding to the property of the natural dynamics of the pendulum-like swing motion, is essential for successful task execution with reduced control effort.

Consider the swing locomotion task on a ladder with the intervals starting from the bar at $d_{ start }=0.42$ m to the target located at $d_{ target }=0.46$ m (cf. Fig. 2). We optimize both the control command $\mathbf{u}$ and the movement duration T. We use $\mathbf{Q}_T = \mathrm {diag}(10000, 10000, 10, 10)$, $\mathbf{R}_1 = \mathrm {diag}(0.0001, 0.0001)$ and $R_2 = 0.01$ for the cost function in (38). The optimized movement duration was $T=0.806$ s.

Figure 3 shows the simulation result of (a) the optimized robot movement, (b) joint trajectories and servo motor positions, and (c) joint torque, spring tension and joint stiffness. In the plots, trajectories of the fixed time horizon ranging $T \in [0.7, 0.75, \ldots , 0.9]$ s are also overlayed for comparison in addition to the case of the optimal movement duration $T = 0.806$ s. In the movement with temporal optimization, the spring tension and the joint stiffness are kept small at the beginning and end of the movement resulting in nearly zero joint torque. This allows the joint to swing passively. The joint torque is exerted only during the middle of the swing by increasing the spring tension as necessary. In contrast, with non-optimal time horizon, larger joint torque and spring tension as well as higher joint stiffness can be observed resulting in the requirement of increased control effort. This result suggests that the natural plant dynamics are fully exploited for the desirable task execution with simultaneous stiffness and temporal optimization.

Fig. 3

Simulation result of the single phase brachiation task with temporal optimization. a Movement of the robot (simulation) with optimal variable stiffness control (optimized duration $T = 0.806$ s). b Joint trajectories and servo motor positions. c Joint torque, spring tension and joint stiffness. In b, c, gray thin lines show the plots for non-optimized T in the range of $T=[0.7, 0.75, \ldots , 0.9]$ s and blue thick lines show the plots for optimized $T=0.806$ s. Note that with temporal optimization, at the beginning and the end of the movement, joint torque, spring tension and joint stiffness are kept small allowing the joint to swing passively in comparison to the non-optimal time cases (Color figure online)

Benefit of stiffness variation

In this section, we investigate the benefit of time-varying stiffness modulation. One of the characteristics of VSAs is its ability to simultaneously modulate joint torque and stiffness. Modulating stiffness effectively alters the properties of the system dynamics such as natural frequency. Thus, the capability of modulating stiffness during the motion can be beneficial for improving the task performance.

We demonstrate the benefit of time-varying modulation of stiffness by comparing optimal variable stiffness control and optimal fixed stiffness control. In optimal variable stiffness control, both the control commands $u_1(t)$ and $u_2(t)$ in $\mathbf{u}=[\;u_1(t),\;u_2(t)\;]^T$ are optimized in a time-varying manner during the movement to independently control the joint torque and the joint stiffness. In optimal fixed stiffness control, the command to the spring pre-tensioning servomotor is fixed to the optimal constant value throughout the movement, i.e., $\mathbf{u}= [\;u_1(t),\;u_2\;]^T$ where $u_2 = \mathrm {const.}$ Note that constant command to the pre-tensioning servomotor $u_2$ does not necessarily mean constant joint stiffness with MACCEPA (Braun et al. 2012). In the case of optimal fixed stiffness control, it was possible to achieve the comparable swing movement for the same intervals of $d_{ start }=0.42$ m and $d_{ target }=0.46$ m as in Sect. 4.3 above. However, in optimal fixed stiffness control incurs a higher cost $J=9.528$ than that of the corresponding optimal variable stiffness case with $J=2.979$.

In addition, we compare the performance of variable and fixed optimal stiffness control in terms of the range of distances that can be reached with the robot. Starting from the bar at the nominal distance $d_{ start }=0.42$ m, we vary the target positions $d_{ target }$ by 0.01 m and optimize control commands and movement duration. When the endeffector position at $t=T_f$ is within a tolerance of 0.01 m from the location of the target, we assume that the trial is successful. With optimal variable stiffness control, the robot was able to reach the target in the range of $d_{ target } \in [0.39, 0.59]$ m (the range of 0.20 m) while with optimal fixed stiffness control, it was $d_{ target } \in [0.42, 0.52]$ m (the range of 0.10 m). These numerical explorations illustrate the benefit of optimal variable stiffness control in terms of the cost and range of distances achieved in swing locomotion in comparison to optimal fixed stiffness control.

Spatio-temporal optimization of multiple swings in brachiation

We evaluate the effectiveness of the proposed approach in robot brachiation that incorporates switching dynamics and multiple phases of the movement. We present numerical simulations and experimental implementation on a physical two-link brachiating robot with VSA.

Brachiating robot model in hybrid dynamics formulation

The dynamics of a two-link brachiating robot with a VSA model including switching (cf. (1)) are given by

$$\begin{aligned} \mathbf{M}_i(\mathbf{q}) \ddot{\mathbf{q}} + \mathbf{C}_i(\mathbf{q}, \dot{\mathbf{q}})\dot{\mathbf{q}} + \mathbf{g}_i(\mathbf{q}) + \mathbf{D}_i \dot{\mathbf{q}} = \left[ \begin{array}{c} 0\\ \tau (\mathbf{q}, \mathbf{q}_m)\\ \end{array} \right] . \end{aligned}$$

(41)

When considering multi-phase movement optimization, we assume that the robot has an asymmetric structure in the dynamics (unequal mass and/or link length), where we have two sets of subsystems denoted by the subscripts $i=1$ (hand 1 grasping) and $i=2$ (hand 2 grasping) as depicted in Fig. 4. The model $i=2$ is the flipped configuration of the model $i=1$ with the parameters used in Sect. 4.1. In this model, the robot has asymmetric configuration with respect to its unequal inertial parameters.

The joint torque by VSA $\tau$ is given in (34) and the system includes the servo motor dynamics in (37). The effective model switches between $i=1$ and $i=2$ interchangeably at the switching instance $T_k$ when the robot grasps the bar (see Fig. 4).

Fig. 4

Hybrid dynamics modelling of a brachiating robot with generic asymmetric structure. The dynamics switches at the transition from a handhold to the next with a discrete state mapping

To formulate the optimization problem, we use the state space representation in (6). At the transition at handhold, an affine discrete state transition $\mathbf{x}^+ = \varvec{\Delta }(\mathbf{x}^-) = \varvec{\Gamma }\mathbf{x}^- + \varvec{\gamma }$ is introduced to shift the coordinate system for the next handhold and reset the joint velocities of the robot to zero, which is defined as

$$\begin{aligned} \varvec{\Gamma }= \mathrm {diag}(\varvec{\Gamma }_1, \ldots , \varvec{\Gamma }_4) \end{aligned}$$

(42)

where

$$\begin{aligned} \varvec{\Gamma }_1 = \left[ \begin{array}{cc} 1 &{} 1\\ 0 &{} -1\\ \end{array} \right] , \varvec{\Gamma }_2 = \left[ \begin{array}{cc} 0 &{} 0\\ 0 &{} 0\\ \end{array} \right] , \varvec{\Gamma }_3 = \varvec{\Gamma }_4 = \left[ \begin{array}{cc} -1 &{} 0\\ 0 &{} 1\\ \end{array} \right] \end{aligned}$$

(43)

and $\varvec{\gamma }= [\;-\pi ,\;0,\;\cdots ,\;0\;]^T$. Note that in this example, we have $\varvec{\Delta }=\varvec{\Delta }^{1,2}=\varvec{\Delta }^{2,1}$.

Simulation results

We consider a brachiating task with multiple phases of the movement as follows: First, the robot swings up from the suspended posture to the target at $d_1=0.40$ m and subsequently moves to the target located at $d_2= 0.42$ m and $d_3=0.46$ m, respectively. The composite cost function to encode this task is given by

$$\begin{aligned} J= & {} \left( \mathbf{y}(T_f) - \mathbf{y}_f^*\right) ^T \mathbf{Q}_{T_f} \left( \mathbf{y}(T_f) - \mathbf{y}_f^*\right) \nonumber \\&+\sum _{j=1}^K \left( \mathbf{y}\left( T_j^-\right) - \mathbf{y}^*_j\right) ^T \mathbf{Q}_{T_j} \left( \mathbf{y}\left( T_j^-\right) - \mathbf{y}^*_j\right) \nonumber \\&+\int _{0}^{T_f} \left( \mathbf{u}^T \mathbf{R}_1 \mathbf{u}+ R_2 F^2 \right) dt + w_T T_1 \end{aligned}$$

(44)

where $K=3$ is the number of phases, $\mathbf{y}= [\;\mathbf{r},\;\dot{\mathbf{r}}\;]^T \in \mathbb {R}^4$ is the position and the velocity of the gripper in the Cartesian coordinates measured from the origin at current handhold, $\mathbf{y}^*$ is the target value when reaching the target $\mathbf{y}^* = [\;\mathbf{r}^*,\;\mathbf{0}\;]^T$ and F is the spring tension in the VSA. Note that this cost function includes the time cost $w_T T_1$ for the swing up maneuver. We use $\mathbf{Q}_T = \mathbf{Q}_{T_j} = \mathrm {diag}(10000, 10000, 10, 10)$, $\mathbf{R}_1 = \mathrm {diag}(0.0001, 0.0001)$ and $R_2 = 0.01$ and $w_T=1$. In addition, we impose constraints on the range of the angle of the second joint during the course of the swing up maneuver as $q_{2_{ min }} \le q_2 \le q_{2_{ max }}$, where $[q_{2_{ min }},q_{2_{ max }}]=[-1.745, 1.745]$ rad, by adding a penalty term to the cost (44). This is introduced considering the physical joint limit of the hardware platform used in this paper.

Fig. 5

Simulation result of the multi-phase brachiation task with temporal optimization. a Optimized multi-phase movement of the robot (simulation). b Joint trajectories and servo motor positions of complete optimization with temporal optimization

Figure 5a shows the sequence of the multi-phase movement of the robot optimized by the proposed algorithm including temporal optimization. The optimized switching instance and total movement duration are $T_1 = 5.259$, $T_2 = 6.033$ and $T_f = 6.835$ s and the total cost is $J = 37.815$. Figure 5b shows the optimized joint trajectories and servo motor positions. Note that at the instance of switching denoted by vertical lines, discrete state transition can be observed in these trajectories due to the definition of the coordinate transformation.

To illustrate the benefit of the proposed multi-phase formulation, we performed movement optimization with a pre-specified nominal (fixed, non-optimal) time horizon with $T_1=5.2$, $T_2=5.9$ and $T_f=6.7$ s using the same cost parameters both in sequential and multi-phase optimization. With sequential individual movement optimization, large overshoot was observed at the end of the final phase movement (distance from the target at $t=T_f$ was 0.0697 m) incurring significantly large total cost of $J=101.053$. In contrast, for the same pre-specified time horizon, by employing multi-phase movement optimization, it was possible to find a feasible solution to reach the target bars. The error at the final swing at $t=T_f$ was 0.0020 m, which was significant improvement compared to the case of individual optimization. The largest error observed in this sequence was 0.0109 m at the end of the first swing up phase. In this case, the total cost was $J = 50.228$. These results demonstrate the benefit of the multi-phase movement optimization in finding optimal control commands and temporal aspect of the movement using the proposed method resulting in lower cost.

Fig. 6

Configuration of the two-link brachiating robot with VSA in CAD drawing

Fig. 7

Experimental result of the single phase locomotion task with the brachiating robot hardware. a Optimized movement of the robot (single phase locomotion). b Joint trajectories and servo motor positions. In b, red and blue thick lines show the experimental data, and gray thin lines show the corresponding simulation result with the optimized planned movement duration $T=0.806$ s presented in Sect. 4.3 (Color figure online)

Hardware platform of a brachiating robot with VSA

The configuration of the brachiating robot with VSA is depicted in Fig. 6. The elbow joint is actuated with a VSA (MACCEPA (Van Ham et al. 2007)) having two servo motors (Hitec HS-7940TH). Each link is equipped with a gripper driven by a single servo motor (Hitec HSR-5990TG) to open and close it through a gear mechanism. The angle of the first link is obtained through an IMU unit (InvenSense MPU-6050) attached to the link. The angle of the second link is measured by a rotary potentiometer (Alps RDC503013A) at the elbow joint. The servo motor positions are measured through direct access to its internal potentiometer. The operating frequency of control and measurement is 1KHz. The length of each link is 0.46 m and the total mass is 1.92 kg. The link parameters are obtained from the CAD model while friction coefficients and the servo motor bandwidth parameters are estimated by fitting the actual responses of the robot. Our numerical exploration showed that with an inadequate mass distribution, it was difficult to find an optimal solution in achieving desired swing locomotion behavior. By this reason, the mass distribution of the robot was chosen to resemble the desirable natural dynamics required for the task (see Table 1 for the parameters).

Experimental results

Figure 7 shows the experimental result of swing locomotion on the ladder with the intervals of $d_{ start }=0.42$ m and $d_{ target }=0.46$ m. The optimized control commands with the optimal movement duration obtained in the corresponding simulation in Sect. 4.3 are used. In Fig. 7a, the movement of the robot is depicted while in Fig. 7b the joint trajectories and servo motor positions are shown. This result corresponds to the simulation in Fig. 3 with the optimal movement duration. In the experiments, we only use the open-loop optimal control command to the servo motors without state feedback as in (Braun et al. 2012).

Figure 8 shows the experimental result of multi-phase movements consisting of swing-up followed by two additional swings which corresponds to the simulation in Fig. 5. The intervals between the target bars are $d_1=0.40$ m, $d_2=0.42$ m and $d_3=0.46$ m. Figure 8a illustrates the movement of the robot moving from left to right while Fig. 8b shows the joint trajectories and servo motor positions. The joint trajectories in the experiment closely match the planned movement in the simulation. The discrepancy is mainly due to the inevitable difference between the analytical model and the hardware system. Due to practical reasons, instantaneous switching cannot be performed with the gripper mechanism of the hardware. Thus, a short halt at the end of each phase was introduced to ensure firm grasping.

Fig. 8

Experimental result of the multi-phase locomotion task with the brachiating robot hardware. a Optimized movement of the robot (multi-phase movement). b Joint trajectories and servo motor positions. In b, red and blue lines show the actual hardware behavior, and gray lines show the corresponding simulation result presented in Sect. 5.2 (Color figure online)

The experiments above are presented in the accompanied video. These results demonstrate the effectiveness and feasibility of the proposed framework in achieving highly dynamic tasks in compliantly actuated robots with variable stiffness capability under real-world conditions.

Multi-phase optimization in hopping with VSA

In this section, we demonstrate the feasibility of the proposed approach on an increasingly challenging task of hopping which includes switching of different mode of dynamics (flight and stance) and more complex discontinuous state transition arising from impact at touch-down. Additional difficulty in this task is to find the flight and stance time for successful task execution which is highly restricted by the underactuated nature of the intrinsic dynamics and the desired task specifications.

We consider the hopping robot model in (Hyon and Emura 2004) with an augmentation of variable compliance elements in the hip and the leg actuators. The objective of optimization is to find appropriate leg and hip stiffness to exploit the passive dynamics and also the required flight and stance time during one locomotion cycle in a periodic movement based on a time-based switching approximation. The obtained controller is then applied to achieve multiple hopping cycles of locomotion on event based switching dynamics. Robustness of the obtained optimal feedback controller will be evaluated by applying external disturbances during the multiple hopping cycles to demonstrate the feasibility of the optimized controller.

Dynamics model of a hopping robot

The hopping dynamics switch between the flight phase and stance phase (with $i=1$: flight and $i=2$: stance) at the switching instance $T_j$ when either touch-down or lift-off conditions are met. The configuration vector of the system is defined as $\mathbf{q}=[x_{ com },y_{ com },\theta ,\phi ,r]^T$ (see Fig. 9).

Fig. 9

Hybrid dynamics of a hopping robot model and locomotion phases during one cycle

The flight dynamics ($i=1$) are given as

$$\begin{aligned} \left\{ \begin{array}{ll} M \ddot{x}_{ com } = 0, &{} M \ddot{y}_{ com } = - Mg \\ J_l\ddot{\theta } = -\tau _{ hip }, &{}J_b\ddot{\phi } = \tau _{ hip } \end{array}\right. \end{aligned}$$

(45)

with $r=r_0$. The stance dynamics ($i=2$) are given as

$$\begin{aligned} \left\{ \begin{array}{l} (J_l+Mr^2) \ddot{\theta }+2 M r \dot{r}\dot{\theta }-Mrg\sin \theta = -\tau _{ hip }\\ J_b\ddot{\phi } = \tau _{ hip } \\ M \ddot{r} - M r \dot{\theta }^2 + Mg\cos \theta = \tau _{ leg } \end{array}\right. \end{aligned}$$

(46)

with $x_{ com }=-r \sin \theta + x_{ foot }$ and $y_{ com } = r \cos \theta + y_{ foot }$. M is the mass of the body, $J_l$ is the leg inertia, $J_b$ is the body inertia, g is the gravitational constant, $r_0$ is the nominal length of the leg spring. $\tau _{ hip }$ and $\tau _{ leg }$ are the torque applied to the hip joint and the force applied to the leg by the VSAs as given in (48) and (49) below, respectively. We use the parameters $M=11.0$ kg, $J_b=2.5$ kgm$^2$, $J_l=0.25$ kgm$^2$ and $r_0=0.7$ m adopted from (Ahmadi and Buehler 1997).

In a general form, the flight and stance dynamics can be written as

$$\begin{aligned} \mathbf{M}_i\ddot{\mathbf{q}}_i + \mathbf{C}_i(\mathbf{q}_i,\dot{\mathbf{q}}_i)\dot{\mathbf{q}}_i + \mathbf{g}_i(\mathbf{q}_i) = \varvec{\tau }_i(\mathbf{q}_i,\mathbf{u}_i) \end{aligned}$$

(47)

where $\mathbf{q}_1 = [x_{ com }, y_{ com }, \theta , \phi ]^T$ and $\mathbf{q}_2 = [\theta , \phi , r]^T$ are the partial configuration vector for the flight and stance phase, respectively.

$\varvec{\tau }_1(\mathbf{q},\mathbf{u}) = [0, 0, -\tau _{ hip }, \tau _{ hip }]^T$ and $\varvec{\tau }_2(\mathbf{q},\mathbf{u}) = [-\tau _{ hip }, \tau _{ hip }, \tau _{ leg }]^T$ are the VSA torque/force applied to each degree of freedom where

$$\begin{aligned} \tau _{ hip }(\mathbf{q},\mathbf{u})= & {} u_1 - u_3(\phi -\theta ) \end{aligned}$$

(48)

$$\begin{aligned} \tau _{ leg }(\mathbf{q},\mathbf{u})= & {} u_2 - u_4(r - r_0) \end{aligned}$$

(49)

and $\mathbf{u}=[u_1,u_2,u_3,u_4]^T$ is the control command vector defined, where $u_1$ is the hip torque, $u_2$ is the leg force, $u_3$ is the hip joint stiffness and $u_4$ is the leg stiffness. The range of the control and stiffness is limited as $\mathbf{u}_{ min } \preceq \mathbf{u}\preceq \mathbf{u}_{ max }$ where $\mathbf{u}_{ min } =[\;-100,\;-100,\;10,\;2000\;]^T$ and $\mathbf{u}_{ max } =[\;100,\;100,\;150,\;25000\;]^T$.

For the purpose of optimization, the dynamics will be formulated in a state space representation of the form of $\dot{\mathbf{x}}=\mathbf{f}_i(\mathbf{x}, \mathbf{u})$ as in (5) with the full state vector $\mathbf{x}=[\;\mathbf{q}^T,\;\dot{\mathbf{q}}^T\;]^T$ and $\mathbf{q}=[x_{ com },y_{ com },\theta ,\phi ,r]^T$. In this hopping robot, we consider a simplified parallel elastic VSA model with direct force/torque and stiffness control as in (Hyon and Emura 2004), which does not include the motor dynamics⁶ (2).

The discontinuous impact map at touch-down is defined as

$$\begin{aligned} \mathbf{x}^{+}=\varvec{\Delta }^{1,2}(\mathbf{x}^{-}) = \left[ \begin{array}{cc} \mathbf{I} &{} \mathbf{0}\\ \mathbf{0} &{} \varvec{\Lambda }(\mathbf{q})\\ \end{array} \right] \mathbf{x}^{-} \end{aligned}$$

(50)

where $\mathbf{x}=[\mathbf{q}^T,\dot{\mathbf{q}}^T]^T$, $\mathbf{q}^+=\mathbf{q}^-$ and $\dot{\mathbf{q}}^+=\varvec{\Lambda }(\mathbf{q}) \dot{\mathbf{q}}^-$. The matrix $\varvec{\Lambda }(\mathbf{q})$ is the transition map between the pre-impact to post-impact velocities based on a rigid body collision model (Grizzle et al. 2001; Rosa et al. 2012). The specific form of the velocity transition map is given in the study of passive running with an additional analysis of energy dissipation at impact (Hyon and Emura 2004). At lift-off, the velocity of the leg is reset to zero as $\dot{r} =0$ at $r=r_0$.

Design of composite cost function

In this paper, we consider a task of achieving periodic movement of continuous hopping which is a repetition of one hopping cycle while exploiting the passive dynamics and the benefits of stiffness modulation. For this purpose, first, we design a composite cost function for one hopping cycle including both the flight and stance phases and the desirable touch-down condition. Then, the obtained controller is applied to achieve multiple cycles.

Consider the following cost function:

$$\begin{aligned} J= & {} (\mathbf{x}(T_f)-\mathbf{x}_0)^T \mathbf{Q}_{T_f}(\mathbf{x}(T_f)-\mathbf{x}_0)+ \Psi \left( \mathbf{x}\left( T_1^-\right) \right) \nonumber \\&+\int _{0}^{T_f}\mathbf{u}^T\mathbf{R}\mathbf{u}\,dt \end{aligned}$$

(51)

where $\mathbf{Q}_{T_f}$ is a positive semi-definite matrix and $\mathbf{R}$ is a positive definite matrix. The purpose of the first term is to achieve periodicity of the trajectory where $\mathbf{x}_0$ denotes the initial state. The second term consists of two criteria:

$$\begin{aligned} \Psi \left( \mathbf{x}\left( T_1^-\right) \right) = Q_{T_1,1} \left( y^{-}_{ foot } - y_{ ground }\right) ^2 + Q_{T_1,2} (\mu ^{-})^2 \end{aligned}$$

(52)

where $Q_{T_1,1}$ and $Q_{T_1,2}$ are positive weights. The first term $Q_{T_1,1} (y^{-}_{ foot } - y_{ ground })^2$ penalizes the height of the foot from the ground $y_{ ground }=0$ to approximately encode the touch-down condition in a time-based formulation. In order to minimize this term, it is important to find an appropriate flight time $T_1$ as the trajectory of the center of mass cannot be directly controlled in the flight phase for a given initial lift-off condition. The second term $Q_{T_2,2} (\mu ^{-})^2$ minimizes energy loss at touch-down where $\mu ^-$ is called the energy dissipation coefficient

$$\begin{aligned} \mu ^{-}&= \dot{x}^{-}_{ com } \cos \theta ^{-} + \dot{y}^{-}_{ com } \sin \theta ^{-}+ r_0 \dot{\theta }^{-}\nonumber \\&=\dot{x}^{-}_{ foot } \cos \theta ^- + \dot{y}^{-}_{ foot } \sin \theta ^- \end{aligned}$$

(53)

motivated from the study of passive running by Hyon and Emura (2004) to find an appropriate leg angle and foot velocity relative to the ground at touch-down. Note that if $\mu ^{-}=0$, there is no energy loss at impact. In the running cost, we minimize the control effort $u_1$ and $u_2$ while small weights are used for penalizing the magnitude of stiffness $u_3$ and $u_4$ for regularization.

The initial conditions are obtained by choosing the desired initial horizontal velocity and lift-off angle of the leg $(\dot{x}_0, \theta _0)$ and computing the remaining parameters with the assumption of synchronization between the oscillatory movements of the leg swing and compression in the passive running model (Ahmadi and Buehler 1997; Hyon and Emura 2004).

Fig. 10

Application of the optimized controller to achieve steady state hopping with multiple cycles. a Movement of the hopping robot (simulation). b Forward velocity, body height, joint angles. c Control commands, and hip and leg stiffness. External perturbations were applied in order to evaluate the robustness of the obtained optimal feedback control law. The robot was able to continue to run after the application of the perturbations without falling over

Simulation results

We choose the desired initial condition at lift off as $\dot{x}_0=2.0$m and $\theta _0=-6.0$ deg ($-0.105$ rad). The rest is obtained based on an approximated condition of passive running (Hyon and Emura 2004) for the nominal model of Ahmadi and Buehler (1997). With this initial condition, the passive dynamics (no control) of the robot can achieve several steps of running as reported by Ahmadi and Buehler (1997) and Hyon and Emura (2004). However, eventually, it will fail since passive running is intrinsically unstable.

Using the proposed method, we simultaneously obtained the optimal feedback control for the control commands $(u_1,u_2)$ and stiffness $(u_3, u_4)$, and found the flight time $T_1$ and the period for one complete cycle $T_f$ for one hopping cycle. The optimized flight time and one hopping cycle were $T_1 = 0.410$ s and $T_f = 0.487$ s. Since the obtained controller is based on an assumption of time-based switching, there could be some mismatch in the exact timing in the switching condition when applied to realistic event based switching dynamics (flight to stance at touch-down $y_{ foot }= y_{ ground }$, stance to flight when $r=r_0$) to achieve multiple cycles of locomotion. One of the benefits of our approach is that it provides a locally optimal feedback control, deviations from the optimal trajectory can be corrected, which will be illustrated in the following examples. These simulation results are presented in the accompanied video.

Comparison to individual phase optimization As a comparison, we optimized the control command, stiffness and the movement duration in a sequential manner individually for the flight phase subsequently followed by the stance phase for one cycle of the movement. The optimized movement duration for the flight phase was $T_{1, ind } = 0.410$ s and for the stance phase was $T_{ stance,ind }=0.080$ s, i.e., the total duration was $T_{ f,ind }=0.490$ s. The total cost for this individual optimization was $J_{ ind }=1.686$ which is comparable to the complete optimization case $J_{ comp }=1.624$ mentioned above. The optimized trajectories, control commands and stiffness profiles are similar between these two cases. However, interestingly, there are notable difference in the robustness of the controller when these two were applied to the event based switching dynamics where the role of the feedback control becomes prominent.

The controller with complete cycle optimization was able to achieve continuous stable running over multiple cycles. However, with the controller obtained by individual optimization, the robot failed to continue to run after 25 steps of hopping. Although this is an empirical observation, this difference presumably came from the difference in the optimal feedback gains. In the complete cycle optimization, the optimal feedback gains take the future goal until the end of the hopping cycle into account including both the flight and stance phases with the via-point and terminal costs. However, in the individual optimization, corrections are made only considering the immediate goal specified by the terminal cost in each phase. This result highlights the benefits of optimizing the whole cycle of the movement in comparison to individually optimizing the movement in a sequential manner. This comparison is demonstrated in the accompanied video.

Robustness against perturbations In this simulation, we evaluate the robustness of the obtained optimal feedback controller by applying external perturbations while the robot is running. At $t=1.0$ s, the robot is pushed forward with $F_x=150$ N and at $t=2.0$ s, a backward perturbation is applied $F_x=-250$ N for the duration of 0.05 s, respectively. Figure 10a depicts the movement of the robot from $t=0.7$ to $t=3.9$ s. Figure 10b show the forward velocity $\dot{x}$ (top), body height $y_{ com }$ (middle), and leg angle $\theta$ and hip angle $\phi$ (bottom) from $t=0$ to $t=6$ s. Figure 10c show the control commands $u_1$ and $u_2$ (top), hip stiffness $u_3$ (center) and leg stiffness $u_4$ (bottom). The simulation result illustrate that after the perturbations, the robot was able to stabilize the periodic running behavior without falling over demonstrating the robustness of the optimal feedback controller and the feasibility of the proposed approach in this problem setting. This result is illustrated in the accompanied video.

Discussion

In this section, we discuss the benefit, practical considerations and possible limitations of the proposed approach.

In Sect. 4.3, benefit of temporal optimization was presented with an example of swing locomotion in a VSA actuated brachiating robot in order to exploit the intrinsic dynamics of the system. Much more significant effect of temporal optimization with a torque controlled brachiating robot in our previous work (Nakanishi et al. 2011) was illustrated in terms of the required control torque to achieve swing motion. With the optimized movement duration, only a very small amount of torque was needed to achieve the task. However, slight change in the movement time resulted in significant increase in the required control command. Furthermore, in the case of periodic movement optimization (Nakanishi et al. 2011), finding an appropriate frequency of the motion matching the natural frequency of the system could reduce the required control effort. These results highlight the benefit of temporal optimization in exploiting the natural dynamics.

In Sect. 5.2, benefit of multi-phase movement optimization was presented in a brachiation example in terms of the improvement in the cost and performance in comparison to individual phase optimization. The main difference from individual phase optimization is that multi-phase optimization takes the future goals into account. The effect of multi-phase optimization in the brachiation example may be less intuitive since every time the robot grasps the bar, joint velocities are reset. In this case, the final positions of the VSA servomotors in each phase can be appropriately determined considering the next phase movement to adjust the spring tension. The example of a via-point reaching task in (Rawlik et al. 2010; Rawlik 2013) demonstrates the benefit of multi-phase optimization more clearly where the velocity and the resultant curvature of the trajectory when passing the via-point can be determined considering the next target position.

One of the practical considerations of the time-based switching approach is the feasibility and accuracy of approximation of the switching condition. In general, accuracy of this approximation largely depends on the nature of the task and the design of the cost function since the switching condition is effectively imposed by the via-point and terminal costs at their corresponding time. In the case of brachiation, considering the design of the gripper in the physical robot, empirically, small error at the endpoint was tolerated assuming that the robot was able to grasp the bar. In the hopping example, as the ground contact condition is more critical, the weights of the cost were empirically adjusted in order to reduce the mismatch. In addition, temporal optimization was helpful in reducing the error by finding an appropriate movement duration which cannot be arbitrarily predetermined. Our empirical results suggest the small mismatch in the switching condition can be alleviated by the use of proper state feedback. It would be of our future interest to evaluate the robustness of the obtained optimal controller against such a mismatch in a more systematic manner.

In terms of feasibility, application of the proposed spatio-temporal optimization approach could be limited to the cases where the switching condition can be represented by a cost function (penalty) with an assumption of known order of switching and we have a reasonable initial estimate of the desirable duration of the movement. If the sequence of the switching is not given a priori, direct trajectory optimization approaches with state-based switching could be more suitable, e.g., (Posa et al. 2014). If we do not consider multi-phase movement optimization as a whole, i.e., when only individual movement optimization is considered, it would be possible to use the event based first-exit strategy as in (Kulchenko and Todorov 2011). However, this would result in a sub-optimal solution overall as discussed in (Rawlik 2013). In these methods, temporal optimization becomes more difficult since the movement time (switching instance) depends on the resultant system’s trajectory as discussed in (Xu and Antsaklis 2004).

Conclusion

In this paper, we have presented a systematic methodology for movement optimization with multiple phases and switching dynamics in robotic systems with VSA with the focus on exploiting intrinsic dynamics of the system. Tasks including switching dynamics and interaction with an environment are approximately modelled as a hybrid dynamical system with time-based switching. We have demonstrated the benefit of simultaneous temporal and variable stiffness optimization leading to reduction in control effort and improved performance. With an appropriate choice of the composite cost function to encode the task, we have demonstrated the effectiveness of the proposed approach in various example tasks in numerical simulations and hardware implementation in a brachiating robot with VSA. Future work will aim at investigation of optimization in biped locomotion with VSA including variable damping (Enoch and Vijayakumar 2016; Radulescu et al. 2012) as well as an extension to learning approaches to address modelling uncertainties of the system dynamics (Mitrovic 2010).