Skip to main content
SpringerLink
Log in

Artificial equilibrium points in binary asteroid systems with continuous low-thrust

  • Original Article
  • Published:
Astrophysics and Space Science Aims and scope Submit manuscript

Abstract

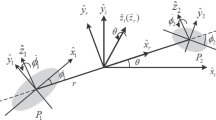
The positions and dynamical characteristics of artificial equilibrium points (AEPs) in the vicinity of a binary asteroid with continuous low-thrust are studied. The restricted ellipsoid–ellipsoid model of binary system is employed for the binary asteroid system. The positions of AEPs are obtained by this model. It is found that the set of the point \(L_{1}\) or \(L_{2}\) forms a shape of an ellipsoid while the set of the point \(L_{3}\) forms a shape like a “banana”. The effect of the continuous low-thrust on the feasible region of motion is analyzed by zero velocity curves. Because of using the low-thrust, the unreachable region can become reachable. The linearized equations of motion are derived for stability’s analysis. Based on the characteristic equation of the linearized equations, the stability conditions are derived. The stable regions of AEPs are investigated by a parametric analysis. The effect of the mass ratio and ellipsoid parameters on stable region is also discussed. The results show that the influence of the mass ratio on the stable regions is more significant than the parameters of ellipsoid.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

References

  • Aliasi, G., Mengali, G., Quarta, A.A.: Artificial equilibrium points for a generalized sail in the circular restricted three-body problem. Celest. Mech. Dyn. Astron. 110(4), 343–368 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Aliasi, G., Mengali, G., Quarta, A.A.: Artificial equilibrium points for electric sail with constant attitude. J. Spacecr. Rockets 50(6), 1295–1298 (2013)

    Article  ADS  MATH  Google Scholar 

  • Aliasi, G., Mengali, G., Quarta, A.A.: Artificial periodic orbits around L1-type equilibrium points for a generalized sail. J. Guid. Control Dyn. 38(9), 1847–1852 (2015)

    Article  ADS  Google Scholar 

  • Baig, S.M., McInnes, C.R.: Artificial three-body equilibria for hybrid low-thrust propulsion. J. Guid. Control Dyn. 31(6), 1644–1655 (2008)

    Article  ADS  Google Scholar 

  • Baig, S.M., Mcinnes, C.R.: Artificial halo orbits for low-thrust propulsion spacecraft. Celest. Mech. Dyn. Astron. 104(4), 321–335 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Bellerose, J., Scheeres, D.J.: Restricted full three-body problem: application to binary system 1999 KW4. J. Guid. Control Dyn. 31(1), 162–171 (2008)

    Article  ADS  Google Scholar 

  • Bombardelli, C., Peláez, J.: On the stability of artificial equilibrium points in the circular restricted three-body problem. Celest. Mech. Dyn. Astron. 109(1), 13–26 (2011)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  • Bookless, J., McInnes, C.R.: Control of Lagrange point orbits using solar sail propulsion. Acta Astronaut. 62(62), 159–176 (2008)

    Article  ADS  Google Scholar 

  • Broschart, S.B., Scheeres, D.J.: Control of hovering spacecraft near small bodies: application to Asteroid 25143 Itokawa. J. Guid. Control Dyn. 28(2), 343–354 (2005)

    Article  ADS  Google Scholar 

  • Dusek, H.M.: Motion in the vicinity of libration points of a generalized restricted three-body model. Prog. Astronaut. Rocket. 17, 37–54 (1966)

    Article  MATH  Google Scholar 

  • Fan, S.: A new extracting formula and a new distinguishing means on the one variable cubic equation. Nat. Sci. J. Hainan Teach. Coll. 2(2), 91–98 (1989)

    Google Scholar 

  • Heiligers, J., Macdonald, M., Parker, J.S.: Extension of Earth–Moon libration point orbits with solar sail propulsion. Astrophys. Space Sci. 361(7), 241 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  • Hou, X.Y., Liu, L.: Collinear libration points with continuous low thrust. Chin. J. Theor. Appl. Mech. 45(2), 265–273 (2013)

    Google Scholar 

  • Kunitsyn, A.L., Perezhogin, A.A.: On the stability of triangular libration points of the photogravitational restricted circular three-body problem. Celest. Mech. Dyn. Astron. 18(4), 395–408 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  • McInnes, C.R.: Artificial Lagrange points for a partially reflecting flat solar sail. J. Guid. Control Dyn. 22(1), 185–187 (1999)

    Article  ADS  Google Scholar 

  • McInnes, C.R., McDonald, A.J.C., Simmons, J.F.L.: Solar sail parking in restricted three-body systems. J. Guid. Control Dyn. 17(2), 399–406 (1994)

    Article  ADS  MATH  Google Scholar 

  • Morimoto, M.Y., Yamakawa, H., Uesugi, K.: Artificial equilibrium points in the low-thrust restricted three-body problem. J. Guid. Control Dyn. 30(5), 1563–1568 (2007)

    Article  ADS  Google Scholar 

  • Ostro, S.J., Margot, J.L., Benner, L.A.: Radar imaging of binary near-Earth asteroid (66391) 1999 KW4. Science 314(5803), 1276–1280 (2006)

    Article  ADS  Google Scholar 

  • Perezhogin, A.A.: Stability of the sixth and seventh libration points in the photogravitational restricted circular three-body problem. J. Vet. Diagn. Invest. 2(4), 481–484 (1976)

    Google Scholar 

  • Perezhogin, A.A., Tureshbaev, A.T.: Stability of coplanar libration points in the photo gravitational restricted three-body problem. Sov. Astron. Lett. 33(4), 445–448 (1989)

    MATH  Google Scholar 

  • Ranjana, K., Kumar, V.: On the artificial equilibrium points in a generalized restricted problem of three bodies. Int. J. Astron. Astrophys. 3(4), 508–516 (2013)

    Article  Google Scholar 

  • Schuerman, D.W.: The restricted three-body problem including radiation pressure. Astrophys. J. 238 337–342 (1980)

    Article  ADS  MathSciNet  Google Scholar 

  • Simmons, J.F., McDonald, A.J.C., Brown, J.C.: The restricted 3-body problem with radiation pressure. Celest. Mech. Dyn. Astron. 35(2), 145–187 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  • Wang, Y.K.: Research on orbit design and optimization of asteroid exploration mission (2016)

  • Waters, T.J., McInnes, C.R.: Solar sail dynamics in the three-body problem: homoclinic paths of points and orbits. Int. J. Non-Linear Mech. 43(6), 490–496 (2008)

    Article  ADS  MATH  Google Scholar 

  • Williams, T., Abate, M.: Capabilities of furlable solar sails for asteroid proximity operations. J. Spacecr. Rockets 46(5), 967–975 (2009)

    Article  ADS  Google Scholar 

  • Yang, H.W., Zeng, X.Y., Baoyin, H.X.: Feasible region and stability analysis for hovering around elongated asteroids with low thrust. Res. Astron. Astrophys. 15(9), 1571–1586 (2015)

    Article  ADS  Google Scholar 

  • Zeng, X.Y., Jiang, F.H., Li, J.F.: Asteroid body-fixed hovering using non-ideal solar sails. Res. Astron. Astrophys. 15(4), 597–607 (2015)

    Article  ADS  Google Scholar 

  • Zeng, X.Y., Gong, S.P., Li, J.F., Alfriend, K.T.: Solar sail body-fixed hovering over elongated asteroids. J. Guid. Control Dyn. 39, 1223–1231 (2016)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The work described in this paper was supported by the National Natural Science Foundation of China (Grant No. 11672126), Innovation Funded Project of Shanghai Aerospace Science and Technology (Grant No. SAST2015036), the Opening Grant from the Key Laboratory of Space Utilization, Chinese Academy of Sciences (LSU-2016-07-01). The authors fully appreciate their financial supports.

Author information

Authors and Affiliations

  1. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Shichao Bu, Shuang Li & Hongwei Yang

  2. Laboratory of Space New Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

    Shichao Bu, Shuang Li & Hongwei Yang

Authors
  1. Shichao Bu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongwei Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuang Li.

Appendix

Appendix

$$\begin{aligned} &{\frac{\partial V}{\partial x} = \frac{\partial U_{s}}{\partial x} + \frac{\partial U_{e}}{\partial x} + \omega^{2}x + u_{x}} \\ &{\phantom{\frac{\partial V}{\partial x}}=\frac{5C_{20s} \{ y^{2} - 2z^{2} + [ x - r ( 1 - \mu ) ]^{2} \} [ x - r ( 1 - \mu ) ]\mu}{ 2 \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial x}=} - \frac{C_{20s} [ x - r ( 1 - \mu ) ]\mu}{ \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial x}=} - \frac{ [ x - r ( 1 - \mu ) ]\mu}{ \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{3}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial x}=} - \frac{15C_{22e} ( 1 - \mu ) ( x + r\mu ) [ - y^{2} + ( x + r\mu )^{2} ]}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{7}{2}}} }\\ &{ \phantom{\frac{\partial V}{\partial x}=}+ \frac{5C_{20e} ( 1 - \mu ) ( x + r\mu ) [ y^{2} - 2z^{2} + ( x + r\mu )^{2} ]}{2 [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial x}=} - \frac{C_{20e} ( 1 - \mu ) ( x + r\mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial x}=} + \frac{6C_{22e} ( 1 - \mu ) ( x + r\mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial x}=} - \frac{ ( 1 - \mu ) ( x + r\mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{3}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial x}=}+ \omega^{2}x + u\cos \theta \cos \varphi }\\ &{\phantom{\frac{\partial V}{\partial x}}= 0, }\\ &{\frac{\partial V}{\partial y} = \frac{\partial U_{s}}{\partial y} + \frac{\partial U_{e}}{\partial y} + \omega^{2}y + u_{y} }\\ &{\phantom{\frac{\partial V}{\partial y}}= \frac{5C_{20s}y \{ y^{2} - 2z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}\mu}{2 \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} - \frac{C_{20s}y\mu}{ \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} - \frac{y\mu}{ \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{3}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} - \frac{15C_{22e}y ( 1 - \mu ) [ - y^{2} + ( x + r\mu )^{2} ]}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} + \frac{5C_{20e}y ( 1 - \mu ) [ y^{2} - 2z^{2} + ( x + r\mu )^{2} ]}{2 [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} - \frac{C_{20e}y ( 1 - \mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} - \frac{6C_{22e}y ( 1 - \mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} - \frac{y ( 1 - \mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{3}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial y}=} + \omega^{2}y + u\cos \theta \sin \varphi }\\ &{\phantom{\frac{\partial V}{\partial y}}= 0, }\\ &{\frac{\partial V}{\partial z} = \frac{\partial U_{s}}{\partial z} + \frac{\partial U_{e}}{\partial z} + u_{z} }\\ &{\phantom{\frac{\partial V}{\partial z}}= \frac{5C_{20s}z \{ y^{2} - 2z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}\mu}{2 \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial z}=} + \frac{2C_{20s}z\mu}{ \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial z}=} - \frac{z\mu}{ \{ y^{2} + z^{2} + [ x - r ( 1 - \mu ) ]^{2} \}^{\frac{3}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial z}=} - \frac{15C_{22e}z ( 1 - \mu ) [ - y^{2} + ( x + r\mu )^{2} ]}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial z}=} + \frac{5C_{20e}z ( 1 - \mu ) [ y^{2} - 2z^{2} + ( x + r\mu )^{2} ]}{2 [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{7}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial z}=}+ \frac{2C_{20e}z ( 1 - \mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{5}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial z}=} - \frac{z ( 1 - \mu )}{ [ y^{2} + z^{2} + ( x + r\mu )^{2} ]^{\frac{3}{2}}} }\\ &{\phantom{\frac{\partial V}{\partial z}=} + u\sin \theta }\\ &{\phantom{\frac{\partial V}{\partial z}}= 0.} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bu, S., Li, S. & Yang, H. Artificial equilibrium points in binary asteroid systems with continuous low-thrust. Astrophys Space Sci 362, 137 (2017). https://doi.org/10.1007/s10509-017-3119-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10509-017-3119-7

Keywords

Search

Navigation