Skip to main content
SpringerLink
Log in

Modeling of migrating grains on asteroid’s surface

  • Original Article
  • Published:
Astrophysics and Space Science Aims and scope Submit manuscript

Abstract

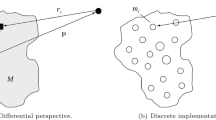
We present a numerical method based on the polyhedral data of asteroid shape for simulation of individual grain’s dynamics around the asteroid surface, with application to migration of regolith material on specific asteroid. Surface gravitational attraction and potential are computed using polyhedral method with a correction on possible singularities; asteroid surface is approximated with continuous quartic Bézier patches based on the division of polyhedral mesh, which provides sufficient geometrical information for the simulation. Orbital motion and surface motion are processed separately by checking if the particle touches or leaves the surface. Collisions are treated as instantaneous point-contact events with the local quartic curved surface. The subpoint is recorded throughout the process to track the ID of the particle. We provide full description of this method including very detailed treatments in numeric. Several basic tests are conducted to examine the performance of this method, and the potential application of this method is also discussed. The test results of seismic regolith migration on crater walls show consistent conclusions with former investigation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Barnett, C.T.: Theoretical modeling of the magnetic and gravitational fields of an arbitrarily shaped three-dimensional body. Geophysics 41, 1353–1364 (1976)

    Article  ADS  Google Scholar 

  • Bellerose, J., Scheeres, D.J.: Dynamics and control for surface exploration of small bodies. In: AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Hawaii, the United States (2008)

    Google Scholar 

  • Belton, M.J.S., Veverka, J., Thomas, P., Helfenstein, P., Simonelli, D., et al.: Galileo encounter with 951 Gaspra: first pictures of an asteroid. Science 257, 1647–1652 (1992)

    Article  ADS  Google Scholar 

  • Belton, M.J.S., Chapman, C.R., Veverka, J., Klaasen, K.P., Harch, A., et al.: First images of asteroid 243 Ida. Science 265, 1543–1547 (1994)

    Article  ADS  Google Scholar 

  • Carr, M., Kirk, R., McEwan, A., Veverka, J., Thomas, P., et al.: The geology of Gaspra. Icarus 107, 61–71 (1994)

    Article  ADS  Google Scholar 

  • Chapman, C.R.: Near-Earth asteroid rendezvous: Eros as the key to the s-type conundrum. Lunar Planet. Sci. XXVI, 229–230 (1995)

    ADS  Google Scholar 

  • Chapman, C.R.: S-type asteroids, ordinary chondrites, and space weathering: the evidence from Galileo’s fly-bys of Gaspra and Ida. Meteorit. Planet. Sci. 31, 699–725 (1996)

    Article  ADS  Google Scholar 

  • Chapman, C.R.: Space weathering of asteroid surfaces. Annu. Rev. Earth Planet. Sci. 32, 539–567 (2004)

    Article  ADS  Google Scholar 

  • Cheng, A.F., Izenberg, N., Chapman, C.R., Zuber, M.T.: Ponded deposits on asteroid 433 Eros. Meteorit. Planet. Sci. 37, 1095–1105 (2002)

    Article  ADS  Google Scholar 

  • Clark, B.E., Fanale, F., Salisbury, J.: Meteorite-asteroid spectral comparison: the effects of comminution, melting and recrystallization. Icarus 97, 288–297 (1992)

    Article  ADS  Google Scholar 

  • Clark, B.E., Hapke, B., Pieters, C., Britt, D.: Asteroid space weathering and regolith evolution. In: Bottke, W.F. Jr., Cellino, A., Paolicchi, P., Binzel, R.P. (eds.) Asteroids III, pp. 585–599. Univ. of Arizona Press, Tucson (2002)

    Google Scholar 

  • Cottingham, C.M., Deininger, W.D., Dissly, R.W., Epstein, K.W., Waller, D.M., et al.: Asteroid surface probes: a low-cost approach for the in situ exploration of small solar system objects. In: IEEE Aerospace Conference, Big Sky, Montana (2009)

    Google Scholar 

  • Farquhar, R., Kawaguchi, J., Russell, C., Schwehm, G., Veverka, J., et al.: Spacecraft exploration of asteroids: the 2001 perspective. In: Bottke, W.F. Jr., Cellino, A., Paolicchi, P., Binzel, R.P. (eds.) Asteroids III, pp. 367–376. Univ. of Arizona Press, Tucson (2002)

    Google Scholar 

  • Feierberg, M.A., Larson, H.P., Chapman, C.R.: Spectroscopic evidence for undifferentiated s-type asteroids. Astrophys. J. 257, 361–372 (1982)

    Article  ADS  Google Scholar 

  • Forsberg, R.: A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modeling. The Department of Geodetic Science and Surveying, Ohio State University, No. 3.55 (1984)

  • Gaffey, M.J., Bell, J.F., Brown, R.H., Burbine, T.H., Piatek, J.L., et al.: Mineralogical variations within the s-type asteroid class. Icarus 106, 573–602 (1993)

    Article  ADS  Google Scholar 

  • Gaskell, R., Neese, C.: NEAR-A-MSI-5-EROSSHAPE-V1.0. NASA Planetary Data System (2008)

  • Geissler, P., Petit, J.M., Durda, D., Greenberg, R., Bottke, W., et al.: Erosion and ejecta reaccretion on 243 Ida and its moon. Icarus 120, 140–157 (1996)

    Article  ADS  Google Scholar 

  • Hamayun, Prutkin, I., Tenzer, R.: The optimum expression for the gravitational potential of polyhedral bodies having a linearly varying density distribution. J. Geod. 83, 1163–1170 (2009)

    Article  ADS  Google Scholar 

  • Housen, K.R., Wilkening, L.L.: Regoliths on small bodies in the solar system. Annu. Rev. Earth Planet. Sci. 10, 355–376 (1982)

    Article  ADS  Google Scholar 

  • Housen, K.R., Wilkening, L.L., Chapman, C.R., Greenberg, R.J.: Asteroidal regoliths. Icarus 39, 317–351 (1979)

    Article  ADS  Google Scholar 

  • Housen, K.R., Schmidt, R.M., Holsapple, K.A.: Crater ejecta scaling laws: fundamental forms based on dimensional analysis. J. Geophys. Res. 88, 2485–2499 (1983)

    Article  ADS  Google Scholar 

  • Hubbert, M.K.: A line-integral method of computing the gravimetric effects of two-dimensional masses. Geophysics 13, 215–225 (1948)

    Article  ADS  Google Scholar 

  • Hudson, R.S.: Three-dimensional reconstruction of asteroids from radar observations. Remote Sens. Rev. 8, 195–203 (1993)

    Article  Google Scholar 

  • Kawaguchi, J., et al.: Hayabusa (MUSES-C)-rendezvous and proximity operation. In: International Astronautic Congress, Fukuoka, Japan (2005)

    Google Scholar 

  • Landshof, J.A., Cheng, A.F.: NEAR mission and science operations. J. Astronaut. Sci. 43, 477–489 (1995)

    Google Scholar 

  • Mantz, A., Sullivan, R., Veverka, J.: Regolith transport in craters on Eros. Icarus 167, 197–203 (2004)

    Article  ADS  Google Scholar 

  • Miyamoto, H., Yano, H., Scheeres, D.J., Abe, S., Barnouin-Jha, O., et al.: Regolith migration and sorting on asteroid Itokawa. Science 316, 1011–1014 (2007)

    Article  ADS  Google Scholar 

  • Moroz, L.V., Fisenko, A.V., Semjonova, L.F.: Optical effects of regolith processes on s-asteroids as simulated by laser shots on ordinary chondrite and other mafic materials. Icarus 122, 366–382 (1996)

    Article  ADS  Google Scholar 

  • Nagy, D., Papp, G., Benedek, J.: The gravitational potential and its derivatives for the prism. J. Geod. 74, 552–560 (2000)

    Article  ADS  MATH  Google Scholar 

  • Neese, C.: Small Body Radar Shape Models V2.0. EAR-A-5-DDR-RADARSHAPE-MODELS-V2.0. NASA Planetary Data System (2004)

  • Nesvorny, D., Bottke, W.F., Vokrouhlicky, D., Chapman, C.R., Rafkin, S.: Do planetary encounters reset surfaces of near Earth asteroids? Icarus 209, 510–519 (2010)

    Article  ADS  Google Scholar 

  • Ostro, S.J., Hudson, R.S., Benner, L.A.M., Giorgini, J.D., Magri, C., et al.: Asteroid radar astronomy. In: Bottke, W.F. Jr., Cellino, A., Paolicchi, P., Binzel, R.P. (eds.) Asteroids III, pp. 151–168. Univ. of Arizona Press, Tucson (2002)

    Google Scholar 

  • Paul, M.K.: The gravity effect of a homogeneous polyhedron for three-dimensional interpretation. Pure Appl. Geophys. 112, 553–561 (1974)

    Article  ADS  Google Scholar 

  • Petrović, S.: Determination of the potential of homogeneous polyhedral bodies using line integrals. J. Geod. 71, 44–52 (1996)

    Article  ADS  MATH  Google Scholar 

  • Plouff, D.: Gravity and magnetic fields of polygonal prisms and application to magnetic terrain corrections. Geophysics 41, 727–741 (1976)

    Article  ADS  Google Scholar 

  • Pohánka, V.: Optimum expression for computation of the gravity field of a homogeneous polyhedral body. Geophys. Prospect. 36, 733–751 (1988)

    Article  ADS  Google Scholar 

  • Rausenberger, O.: Lehrbuch der Analytischen Mechanik I.B.G. Teubner, Leipzig (1888)

    MATH  Google Scholar 

  • Richard, P.B., Alessandro, M., Sihane, M., Francesca, E.D., Mirel, B., et al.: Earth encounters as the origin of fresh surfaces on near-Earth asteroids. Nature 463, 331–334 (2010)

    Article  Google Scholar 

  • Richardson, J.E.: Cratering saturation and equilibrium: a new model looks at an old problem. Icarus 204, 697–712 (2009)

    Article  ADS  Google Scholar 

  • Richardson, J.E.: Regolith generation, retention, and movement on asteroid surfaces: early modeling results. In: 42nd Lunar and Planetary Science Conference, Texas, the United States (2011)

    Google Scholar 

  • Richardson, D.C., Leinhardt, Z.M., Melosh, H.J., Bottke, J.W.F., Asphaug, E.: Gravitational aggregates: evidence and evolution. In: Bottke, W.F. Jr., Cellino, A., Paolicchi, P., Binzel, R.P. (eds.) Asteroids III, pp. 501–515. Univ. of Arizona Press, Tucson (2002)

    Google Scholar 

  • Richardson, J.E., Melosh, H.J., Greenberg, R.: Imapct-induced seismic activity on asteroid 433 Eros: a surface modification process. Science 306, 1526–1529 (2004)

    Article  ADS  Google Scholar 

  • Richardson, J.E., Melosh, H.J., Lisse, C.M., Carcich, B.: A ballistics analysis of the deep impact ejecta plume: determining comet Tempel 1’s gravity, mass, and density. Icarus 190, 357–390 (2007)

    Article  ADS  Google Scholar 

  • Richardson, D.C., Walsh, K.J., Murdoch, N., Michel, P.: Numerical simulations of granular dynamics: I. Hard-sphere discrete element method and tests. Icarus 212, 427–437 (2011)

    Article  ADS  Google Scholar 

  • Rosato, A., Strandburg, K.J., Prinz, F., Swendsen, R.H.: Why the Brazil nuts are on top: size segregation of particulate matter by shaking. Phys. Rev. Lett. 58, 1038–1040 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  • Russel, C.T., Raymond, C.A., Fraschetti, T.C., Rayman, M.D., Polanskey, C.A., et al.: Dawn mission and operations. In: Asteroids, Comets, Meteors Proceedings IAU Symposium, Búzios, Brazil (2005)

    Google Scholar 

  • Saito, J., et al.: Detailed images of asteroid 25143 Itokawa from Hayabusa. Science 312, 1341–1344 (2006)

    Article  ADS  Google Scholar 

  • Scheeres, D.J., Ostro, S.J., Hudson, R.S., De Jong, E.M., Suzuki, S.: Dynamics of orbits close to asteroid 4179 Toutatis. Icarus 132, 53–79 (1998)

    Article  ADS  Google Scholar 

  • Scheeres, D.J., Abe, M., Yoshikawa, M., Nakamura, R., Gaskell, R.W., et al.: The effect of YORP on Itokawa. Icarus 188, 425–429 (2007)

    Article  ADS  Google Scholar 

  • Scheeres, D.J., Hartzell, C.M., Sánchez, P., Swift, M.: Scaling forces to asteroid surfaces: the role of cohesion. Icarus 210, 968–984 (2010)

    Article  ADS  Google Scholar 

  • Schwartz, S.R., Richardson, D.C., Michel, P.: An implementation of the soft-sphere discrete element method in a high-performance parallel gravity tree-code. Granul. Matter 14, 363–380 (2012)

    Article  Google Scholar 

  • Shirman, L.A., Séquin, C.H.: Local surface interpolation with Bézir patches. Comput. Aided Geom. Des. 4, 279–295 (1987)

    Article  MATH  Google Scholar 

  • Shirman, L.A., Séquin, C.H.: Local surface interpolation with Bézir patches: errata and improvements. Comput. Aided Geom. Des. 8, 217–221 (1991)

    Article  MATH  Google Scholar 

  • Sullivan, R., Greeley, R., Pappalardo, R., Asphaug, E., Moore, J., et al.: Geology of 243 Ida. Icarus 120, 119–139 (1996)

    Article  ADS  Google Scholar 

  • Thomas, F.B., Stephen, T.L.: Differential Geometry of Curves and Surfaces. AK Peters, Wellesley (2010)

    MATH  Google Scholar 

  • Thomas, P.C., et al.: Eros: shape, topography, and slope processes. Icarus 155, 18–37 (2002)

    Article  ADS  Google Scholar 

  • Tsoulis, D., Petrović, S.: On the singularities of the gravity field of a homogeneous polyhedral body. Geophysics 66, 535–539 (2001)

    Article  ADS  Google Scholar 

  • Veverka, J., et al.: Imaging of small-scale features on 433 Eros from NEAR: evidence for a complex regolith. Science 292, 484–488 (2001a)

    Article  ADS  Google Scholar 

  • Veverka, J., Thomas, P.C., Robinson, M., Murchie, S., Chapman, C., et al.: Imaging of small-scale features on 433 Eros from NEAR: evidence for a complex regolith. Science 292, 484–488 (2001b)

    Article  ADS  Google Scholar 

  • Werner, R.A.: The gravitational potential of a homogeneous polyhedron or don’t cut corners. Celest. Mech. Dyn. Astron. 59, 253–278 (1994)

    Article  ADS  MATH  Google Scholar 

  • Werner, R.A., Scheeres, D.J.: Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia. Celest. Mech. Dyn. Astron. 65, 313–344 (1997)

    Article  ADS  MATH  Google Scholar 

  • Wilson, J.P.: The Handbook of Geographic Information Science. Wiley/Blackwell (2007)

  • Yeomans, D.K., et al.: Estimating the mass of asteroid 253 Mathilde from tracking data during the near flyby. Science 278, 2106–2109 (1997)

    Article  ADS  Google Scholar 

  • Zuber, M.T., et al.: The shape of 433 Eros from the NEAR-shoemaker laser rangefinder. Science 289, 2097–2101 (2000)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Basic Research Program of China (973 Program, 2012CB720000).

Author information

Authors and Affiliations

  1. School of Aerospace, Tsinghua University, Mengminwei Sci.&Tech. Building N904, 100084, Beijing, China

    Yang Yu

  2. School of Aerospace, Tsinghua University, Mengminwei Sci.&Tech. Building N903, 100084, Beijing, China

    Hexi Baoyin

Authors
  1. Yang Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hexi Baoyin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yang Yu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, Y., Baoyin, H. Modeling of migrating grains on asteroid’s surface. Astrophys Space Sci 355, 43–56 (2015). https://doi.org/10.1007/s10509-014-2140-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10509-014-2140-3

Keywords

Search

Navigation