Skip to main content
SpringerLink
Log in

Resonance in the earth-moon system around the sun including earth’s equatorial ellipticity

  • Original Article
  • Published:
Astrophysics and Space Science Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

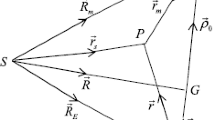
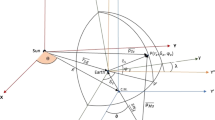
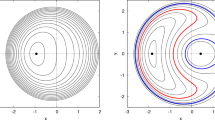
We have investigated the resonances in the earth-moon system around the sun including earth’s equatorial ellipticity. The resonance resulting from the commensurability between the mean motion of the moon and Γ (angle measured from the minor axis of the earth’s equatorial ellipse to the projection of the moon on the plane of the equator) is analyzed. The amplitude and the time period of the oscillation have been determined by using the procedure of Brown and Shook. We have shown the effects of Γ on the amplitude and the time period of the resonance oscillation using the data of the moon. It is observed that the amplitude decreases and the time period also decreases as Γ increases from 0∘ to 45∘.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Abd EI-Salam, F.A., Abdel-Aziz, Y.A., EI-Saftawy, M., Radwan, M.: Analysis of lunisolar resonances in an artificial satellite orbits. Appl. Math. Sci. 2(21), 1013–1021 (2008)

    MathSciNet  Google Scholar 

  • Bhatnagar, K.B., Mehra, M.: The motion of a geosynchronous satellite-I. Indian J. Pure Appl. Math. 17(12), 1438–1452 (1986)

    ADS  MATH  Google Scholar 

  • Breiter, S.: Lunisolar apsidal resonances at low satellite orbits. Celest. Mech. Dyn. Astron. 74, 253–274 (1999)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Breiter, S.: The prograde C7 resonance for Earth and Mars satellite orbits. Celest. Mech. Dyn. Astron. 77, 201–214 (2000)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Breiter, S.: On the coupling of lunisolar resonances for Earth satellite orbits. Celest. Mech. Dyn. Astron. 80, 1–20 (2001)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Brown, E.W., Shook, C.A.: Planetary Theory. Cambridge University Press, Cambridge (1933)

    MATH  Google Scholar 

  • Cook, G.E.: Luni-solar perturbations of the orbit of an Earth satellite. Geophys. J. R. Astron. Soc. 6(3), 271–291 (1962)

    Article  MATH  Google Scholar 

  • Hughes, S.: Earth satellite orbits with resonant lunisolar perturbations. 1. Resonances dependent only on inclination. Proc. R. Soc. Lond. Ser. A 372, 243–264 (1980)

    Article  ADS  Google Scholar 

  • Radwan, M.: Résonance caused by the Luni-Solar Attractions on a Satellite of the Oblate Earth. Astrophys. Space Sci. 282, 551–562 (2002)

    Article  ADS  Google Scholar 

  • Yadav, S., Aggarwal, R.: Resonance in a geo-centric satellite due to Earth’s equatorial ellipticity. Astrophys. Space Sci. (2013). doi:10.1007/s10509-013-1515-1

    Google Scholar 

Download references

Acknowledgement

We are thankful to the Centre for Fundamental Research in Space Dynamics and Celestial Mechanics (CFRSC) for providing all facilities for this research work.

Author information

Authors and Affiliations

  1. Maharaja Agrasen College, Department of Mathematics, University of Delhi, Delhi, India

    Sushil Yadav

  2. Sri Aurobindo College, Department of Mathematics, University of Delhi, New Delhi, India

    Rajiv Aggarwal

Authors
  1. Sushil Yadav
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rajiv Aggarwal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajiv Aggarwal.

Appendices

Appendix A

$$\begin{aligned} &{P_{1} = 2 - 3\sin^{2}\alpha_{m}, } \\ &{P_{2} = \bigl( 2 - 3\sin^{2}\alpha_{m} \bigr)^{2}, } \\ &{P_{3} = \bigl( 1 + \cos^{2}\alpha_{m} \bigr) \bigl( 1 + \cos^{2}\varepsilon \bigr),} \\ &{P_{4} = 2\sin^{2}\varepsilon \sin^{2} \alpha_{m}, } \\ &{P_{5} = - \frac{1}{2}\sin 2\varepsilon \sin 2 \alpha_{m}, } \\ &{P_{6} = \frac{1}{2}\sin^{2}\varepsilon \sin^{2}\alpha_{m},} \\ &{P_{7} = \sin^{2}\varepsilon \sin^{4} \frac{\alpha_{m}}{2},} \\ &{P_{8} = - \sin 2\varepsilon \sin \alpha_{m} \sin^{2}\frac{\alpha_{m}}{2},} \\ &{P_{9} = \frac{1}{2} \bigl( 2 - 3\sin^{2} \varepsilon \bigr)\sin^{2}\alpha_{m}, } \\ &{P_{10} = \sin 2\varepsilon \sin \alpha_{m} \cos^{2}\frac{\alpha_{m}}{2}, } \\ &{P_{11} = \sin^{2}\varepsilon \cos^{4} \frac{\alpha_{m}}{2}, } \\ &{P_{12} = \sin^{2}\alpha_{m}, } \\ &{P_{13} = \sin^{2}\alpha_{m} \bigl( 2 - 3 \sin^{2}\alpha_{m} \bigr), } \\ &{P_{14} = \frac{1}{2}\sin^{2} \alpha_{m}, } \\ &{P_{15} = \cos^{4}\frac{\alpha_{m}}{2}, } \\ &{P_{16} = \sin^{4}\frac{\alpha_{m}}{2}, } \\ &{P_{17} = \frac{3}{8} \bigl( 2 - \sin^{2} \alpha_{m} \bigr) \bigl( 2 + 3\sin^{2}\alpha_{m} \bigr), } \\ &{P_{18} = \frac{3}{8}\sin^{2} \alpha_{m} \bigl( 2 - 3\sin^{2}\alpha_{m} \bigr), } \\ &{P_{19} = P_{5} + P_{6}, } \\ &{P_{20} = P_{7} + P_{8} + P_{9} + P_{10} + P_{11}. } \end{aligned}$$

Appendix B

$$\begin{aligned} &{Q_{1} = \cos \varepsilon \cos \alpha_{m}, } \\ &{Q_{2} = - \sin^{2}\varepsilon \sin^{4} \frac{\alpha_{m}}{2}, } \\ &{Q_{3} = \sin 2\varepsilon \sin \alpha_{m} \sin^{2}\frac{\alpha_{m}}{2}, } \\ &{Q_{4} = - \frac{1}{2} \bigl( 2 - 3\sin^{2} \varepsilon \bigr)\sin^{2}\alpha_{m}, } \\ &{Q_{5} = - \sin 2\varepsilon \sin \alpha_{m} \cos^{2}\frac{\alpha_{m}}{2}, } \\ &{Q_{6} = - \sin^{2}\varepsilon \cos^{4} \frac{\alpha_{m}}{2}, } \\ &{Q_{7} = \sin^{2}\alpha_{m}, } \\ &{Q_{8} = \sin^{2}\alpha_{m} \bigl( 2 - 3 \sin^{2}\alpha_{m} \bigr), } \\ &{Q_{9} = \cos^{4}\frac{\alpha_{m}}{2}, } \\ &{Q_{10} = \sin^{4}\frac{\alpha_{m}}{2}, } \\ &{Q_{11} = \frac{1}{4}\sin^{2} \alpha_{m} \bigl( 2 - 3\sin^{2}\alpha_{m} \bigr), } \\ &{Q_{12} = \sin \alpha_{m}\sin \varepsilon. } \end{aligned}$$

Appendix C

$$\begin{aligned} &{K_{1} = \frac{ ( GM_{E} )}{a^{4} ( 1 - e^{2} )^{4}} - \frac{P_{1}\dot{\phi}^{2}}{4a ( 1 - e^{2} )} - \frac{9 ( GM_{E} )J_{2}^{ ( 2 )}R_{0}^{2}P_{3}}{4a^{6} ( 1 - e^{2} )^{6}}, } \\ &{\begin{aligned} K_{2} & = \biggl[ \frac{4 ( GM_{E} )}{a^{4} ( 1 - e^{2} )^{4}} - \frac{P_{1}\dot{\phi}^{2}}{4a ( 1 - e^{2} )} - \frac{27 (GM_{E} )J_{2}^{ ( 2 )}R_{0}^{2}P_{3}}{2a^{6} ( 1 - e^{2} )^{6}} \\ &\quad {}- \frac{3P_{12}\dot{\phi}^{2}}{8a ( 1 - e^{2} )} \biggr]e,\end{aligned} } \\ &{K_{3} = - \frac{3P_{12}\dot{\phi}^{2}}{4a ( 1 - e^{2} )}, } \\ &{K_{4} = - \frac{3eP_{12}\dot{\phi}^{2}}{8a ( 1 - e^{2} )},} \\ &{K_{5} = - \frac{9 ( GM_{E} )J_{2}^{ ( 2 )}R_{0}^{2}P_{4}}{4a^{6} ( 1 - e^{2} )^{6}} - \frac{27n^{2}J_{2}^{ ( 2 )}R_{0}^{2}P_{19}}{2a^{3} ( 1 - e^{2} )^{3}},} \\ &{\begin{aligned}K_{6} = K_{7} & = - \frac{27 ( GM_{E} )J_{2}^{ ( 2 )}R_{0}^{2}eP_{4}}{4a^{6} ( 1 - e^{2} )^{6}} \\ &\quad {}-\frac{81n^{2}J_{2}^{ ( 2 )}R_{0}^{2}e}{4a^{3} ( 1 - e^{2} )^{3}} \biggl( P_{19} + \frac{1}{2}P_{20} \biggr), \end{aligned}} \\ &{K_{8} = - \frac{81n^{2}J_{2}^{ ( 2 )}R_{0}^{2}e}{8a^{3} ( 1 - e^{2} )^{3}}P_{20},} \\ &{K_{9} = - \frac{3P_{14}\dot{\phi}^{2}}{2a ( 1 - e^{2} )}, } \end{aligned}$$
$$\begin{aligned} &{K_{10} = - \frac{3P_{15}\dot{\phi}^{2}}{2a ( 1 - e^{2} )}, } \\ &{K_{11} = - \frac{3P_{16}\dot{\phi}^{2}}{2a ( 1 - e^{2} )}, } \\ &{K_{12} = - \frac{3e\dot{\phi}^{2}}{4a ( 1 - e^{2} )} ( P_{14} + P_{16} ), } \\ &{K_{13} = - \frac{3e\dot{\phi}^{2}}{4a ( 1 - e^{2} )} ( P_{14} + P_{15} ), } \\ &{K_{14} = - \frac{3e\dot{\phi}^{2}P_{15}}{4a ( 1 - e^{2} )}, } \\ &{K_{15} = - \frac{3e\dot{\phi}^{2}P_{16}}{4a ( 1 - e^{2} )}. } \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yadav, S., Aggarwal, R. Resonance in the earth-moon system around the sun including earth’s equatorial ellipticity. Astrophys Space Sci 348, 367–375 (2013). https://doi.org/10.1007/s10509-013-1587-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10509-013-1587-y

Keywords

Search

Navigation