1 Introduction

The omnipresence of dusty plasmas has engendered a lot of interest over the past two decades (Goertz 1989; Shukla 2001). A dusty plasma is defined as a normal electron-ion plasma with an additional constituent of micron or submicron sized particles. A dusty plasma distinguishes itself from ordinary plasmas in various ways. The charged dust particles introduce a wide spectrum of new phenomena associated with waves and instabilities (Shukla and Mamun 2002, 2003; Rao et al. 1990; Shukla and Silin 1992; Varma et al. 1993; Melandso 1996; Salimullah 1996), and give rise to different interesting phenomena in astrophysical and space environments. Examples include cometary comae and tails, planetary rings, the interstellar medium, the lower ionosphere, plasma processing devices, limiter regions of fusion plasmas, etc. (Mendis 1991; Nakano 1998; Zweibel 1999). It has been found both theoretically and experimentally that the presence of these extremely massive and highly charged dust grains in a plasma can modify the behavior of the usual waves and instabilities (de Angelis et al. 1989, 1994; Bingham et al. 1991), whereas the dust charge dynamics gives rise to the introduction of new eigen modes (D’Angelo 1990, 1995; Rosenberg 1993; Shukla 1993; Rao 1995; Barkan et al. 1995). The low frequency dust-acoustic mode is among one of them where the dust particle mass provides the inertia and the pressures of inertialess ions and electrons provide the restoring force.

It is fairly well established that all plasma systems, particularly the dusty plasma systems, always contain some region of inhomogeneity capable of causing drift motions and associated waves in a magnetized dusty plasma. The conventional electrostatic drift waves involve a two-dimensional ion motion in a plane perpendicular to the external magnetic field \(B_{0} \hat{\mathbf{z}}\), along with the Boltzmann distributed inertialess electrons. Thus, the low-frequency (by comparison with the ion gyrofrequency ω ci =eB 0/m i c) waves having parallel (meaning along B 0) phase velocity much smaller than the electron thermal velocity arise due to a balance between the time derivative density fluctuations and the E×B 0 convection of the unperturbed density. The dispersion of the drift waves is provided by the ion polarization drift.

Shock waves are formed owing to the delicate balance between the non-linearity (causing wave steepening) and dissipation (e.g., caused by viscosity, collisions, wave particle interaction, etc.). When the wave breaking due to non-linearity is balanced by the combined effect of dispersion and dissipation, a monotonic or oscillatory dispersive shock wave is generated in a plasma (Shukla and Mamun 2003). Numerous papers have investigated the effects of various dissipative processes on the propagation of ion inertia driven waves both in homogeneous and inhomogeneous plasmas. Ostrikov et al. (1999) studied the current driven ion acoustic instability in a collisional dusty plasma and found that the threshold for the excitation of the dust ion-acoustic waves could become higher on account of the large dissipation rate induced by the dust particles. The effects of the electrons, ions, and neutrals as well the dust charge fluctuation on the ion acoustic waves have also been investigated (Vladimirov et al. 1999, 2003). The nonlinear propagation of drift waves in multicomponent plasmas has also been studied in recent years with regard to space, astrophysical, and laboratory plasmas (Saleem 2005; Mirza et al. 2007; Masood et al. 2008, 2009a, 2009b; Masood 2010).

The satellite observations of space plasmas clearly indicate the presence of ion and electron populations which are far away from their thermodynamic equilibrium (Shukla et al. 1986; Ghosh and Bharuthram 2008; Smets et al. 1998; Berthomier et al. 2000). Over the last two decades, a great deal of attention has been paid to nonextensive statistic mechanics based on the deviations of Boltzmann–Gibbs–Shannon (BGS) entropic measure. A suitable nonextensive generalization of the BGS entropy for statistical equilibrium was first recognized by Renyi (1955) and subsequently proposed by Tsallis (1988), suitably extending the standard additivity of the entropies to the nonlinear, nonextensive case where one particular parameter, the entropic index q, characterizes the degree of nonextensivity of the considered system (q=1 corresponds to the standard, extensive, B-G-S statistics). The two commonly adopted distribution functions for describing the plasmas that are removed from the Maxwellian profile are the kappa distribution, characterized by the κ parameter, and the highly non-Maxwellian distribution profile with bump on the tail proposed by Cairns et al. (1995). The κ distribution has the power-law form and deviates only moderately in the tail from the Maxwellian profile while the distribution of Cairns et al. (1995) exhibits non-monotonic feature in the suprathermal components. Both distributions have been observed to exist in space plasma environments (Christon et al. 1988; Smets et al. 1998; Lui 2006) and applied to the study of certain types of acoustic solitons. Cairns et al. (1995) showed that the presence of a non-Maxwellian distribution of electrons could change the nature of ion acoustic solitary structures to allow for the existence of structures observed by the Freja and Viking satellites (Dovner et al. 1994). The superthermal particles are also well described by the kappa distributions, which involve the Maxwellian core and a high-energy tail component of the power-law form. The use of the kappa-distribution function was first introduced by Vasyliunas (1968) to fit OGO 1 and OGO 2 solar wind data. This is an empirical fit to the observed particle distributions. Since then, it has been widely adopted by various researchers (Hellberg et al. 2009) (and the references therein) to examine the effect of superthermal distributions on linear and nonlinear structures in ion and dust-acoustic regimes. Very recently, the nonlinear structures in electron-ion plasmas with kappa distributed electrons have also been studied (Choi et al. 2011). However such investigations have not been made in inhomogeneous plasmas.

In this paper, we study the linear and nonlinear propagation characteristics of electrostatic waves in dust-electron-ion (DEI) inhomogeneous magnetoplasmas in the presence of non-Maxwellian ions and Maxwellian electrons. The dissipative effect appears due to the collisions of the dust with the neutrals in the background. This paper is organized as follows. In Sect. 2, we present the basic set of fluid equations for the system under consideration and the linear propagation characteristics of the dispersive dust drift waves are presented in Sect. 3. In Sect. 4, a nonlinear equation is derived in the small amplitude limit which reduces to a Korteweg-de Vries-Burgers (KdVB)-like equation in the comoving frame whose solution is found using the tangent hyperbolic method. In Sect. 5, the results are presented and discussed. Finally, in Sect. 6, the conclusion of the present investigation is presented.

2 Basic set of equations

We consider the plasma consisting of electrons, ions and negatively charged dust fluids immersed in a constant external magnetic field \(\mathbf{B}_{0}=B_{0}\hat{z}\). We use Cartesian coordinates (x, y, z). The wave propagation is assumed to be in the y-direction and the equilibrium density gradient is assumed to be in the x-direction. In steady state plasma quasineutrality remains valid. In equilibrium, we have

$$ n_{i0}\simeq n_{e0}+Z_{d}n_{d0}, $$
(1)

where Ω d =eZ d B 0/m d c is the dust Larmor frequency, n i0, n e0, and n d0 are the equilibrium number densities of ions, electrons, and negatively charged dust particles respectively, and Z d is the charge of the dust.

The equation of motion for dust particles is

$$ m_{d}n_{d}\frac{d\mathbf{v}_{d}}{dt}=-en_{d}Z_{d} \biggl(\mathbf{E}+\frac{1}{c}\mathbf{v}_{d}\times \mathbf{B}_{0}\biggr)-m_{d}n_{d} \nu_{nd}\mathbf{v}_{d}, $$
(2)

where ν nd is dust-neutral collision frequency. The frequency of collisions is ν nd ≈n〈σv〉 where n is the number density of particles, denotes the average over particles of all random velocities v in a Maxwellian-like distribution, and the particles are imagined to be identical spheres of cross-sectional area σ.

The perpendicular velocity component of dust gives

(3)

using the drift approximation |∂/∂t|≪Ω d which gives the ordering as given in the above equation. is the E×B drift, is the dust polarization drift, is the collisional drift, and . Ignoring the parallel motion, the dust continuity equation can be written as

(4)

where \(\tilde{n}_{d}\) is the perturbed dust number density. Ions are taken as non-Maxwellian and electrons are assumed to follow Boltzmann distribution on the dust time scale and are expressed as

$$ n_{i}= \left\{\begin{array}{l} n_{i0} [ 1-\varTheta_{1} \frac{e\varphi }{T_{i}}+\frac{\varTheta_{2}}{2}\frac{e^{2}\varphi^{2}}{T_{i}^{2}} ]\\[4pt] \quad \text{for Cairns distributed ions}\\[4pt] n_{i0} [ 1- \varTheta_{1}\frac{e\varphi }{T_{i}}+\frac{\varTheta_{2}}{2}\frac{e^{2}\varphi^{2}}{T_{i}^{2}}]\\[4pt] \quad \text{for Kappa distributed ions} \end{array}\right. $$

where

where Γ=4α/(1+3α), and α is a parameter that determines the population of the non-thermal ions, and

$$ n_{e}=n_{e0} \biggl[ 1+\frac{e\varphi }{T_{e}}+ \frac{1}{2}\frac{e^{2}\varphi^{2}}{T_{e}^{2}} \biggr] $$

where n i and n e are the total number densities (which contains both the equilibrium and perturbed values) of ions and electrons. The quasineutrality condition i.e. \(\tilde{n}_{i}-\tilde{n}_{e}=Z_{d}\tilde{n}_{d}\) in the normalized form becomes

$$ \frac{\tilde{n}_{d}}{n_{d0}}=-\varPhi +\frac{1}{2}\beta \varPhi^{2} $$
(5)

where

3 Linear wave analysis

Assuming that the perturbations are proportional to exp[i(k y y−ωt)] in the linear case, the algebraic manipulation of (4) and (5) yields the following general dispersion relation for the dust drift waves

$$ \omega \bigl(1+\rho_{d}^{2}k_{\bot }^{2} \bigr)-\omega_{d}^{\ast }+i\nu_{nd} \rho_{d}^{2}k_{\bot }^{2}=0, $$
(6)

where ρ d =c d /Ω d is the dust Larmor radius, \(c_{d}= \sqrt{T_{eff}/m_{d}}\) is the dust acoustic speed, \(\omega_{d}^{\ast }=v_{d}^{\ast }k_{y}\) is the drift frequency, \(v_{d}^{\ast }\) is the diamagnetic drift velocity and is given by (cT eff /eB 0)κ nd , where κ nd =(1/n d0)dn d0/dx or d(lnn d0)/dx, and k ⊥=k y . If we ignore the dissipation, we obtain

$$ \omega =\frac{\omega_{d}^{\ast }}{ ( 1+\rho_{d}^{2}k_{\bot }^{2} ) }. $$
(7)

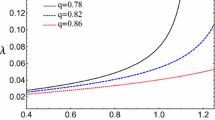
Since the dust Larmor radius contains the dust acoustic speed, therefore, it can easily be seen that a change in the effective temperature, T eff , owing to the non-Maxwellian distributions would alter the frequency of the dust drift waves. The effect of the Cairns, Kappa and Maxwellian distributed ions on dust drift wave as a function of k y is shown in Fig. 1. It is observed that the frequency of the dust drift wave is greatest for the Cairns, intermediate for Kappa and the least for the Maxwellian distributed ions. We have plotted the dispersion relations derived above for some typical plasma parameters found in Saturn’s E rings (Shukla and Mamun 2002) i.e., n d0=10−7 cm−3, n e0=10 cm−3, m d =10−16 g, B 0=0.2 G, T e =105–106 K. We also assume that T i =0.1T e , κ nd =k y /10.

Fig. 1
figure 1

Dispersion relation for the dust drift wave as a function of k y , where α=0.2 (thin solid), α=0.3 (thin dotted) and α=0.4 (thick dotted) for Cairns distributed ions (a) and κ=1.5 (thin solid) and κ=3.0 (dotted) for Kappa distributed ions (b) and the thick solid line is for Maxwellian distribution for both the cases

Full size image

4 Nonlinear wave analysis

In order to investigate the nonlinear structure formation, we proceed as follows. Using (5), the dust continuity equation (i.e. Eq. (4)) becomes

(8)

where χ=[(Θ 1 n i0/T i +n e0/T e )κ nd −(Θ 1 κ ni n i0/T i +κ ne n e0/T e )]/(Θ 1 n i0/T i +n e0/T e ). To find the stationary solution of (8), we transform by introducing the variable ξ=(y−ut) (Where the variable ξ is normalized by the dust Larmor radius and u is the velocity of the nonlinear structure) and obtain the following Korteweg-de Vries-Burgers (KdVB)-like equation for the nonlinear dispersive dust drift shock waves,

(9)

There are a number of methods to solve the nonlinear partial differential equations (NLPDE’s), for instance, inverse scattering method (Ablowitz and Clarkson 1991), Hirota bilinear formalism (Hirota 1971), Backlund transformation (Miura 1978), tanh (Malfliet 1992) etc. However, when the partial differential equation in a system is formed by the combined effect of dispersion and dissipation, the most convenient and efficient method to solve the NLPDE is tanh method (Malfliet 2004). Using the tangent hyperbolic method, (9) in the comoving frame of the nonlinear structure admits the following shock solution

(10)

where the nonlinear velocity u is

$$ u=\frac{1}{2} \biggl[ v_{d}^{\ast }+\sqrt{ \frac{24}{25}\rho_{d}^{2}\nu_{nd}^{2}+ \bigl( v_{d}^{\ast } \bigr)^{2}} \biggr] $$
(11)

Note that the advantage of using tangent hyperbolic method is that it gives us the velocity of the nonlinear structure in terms of the plasma parameters of the system under consideration. The above equation shows that the nonlinear dispersive drift wave potential depends upon the temperatures of electrons and ions, magnetic field strength, density inhomogeneity and the propagation velocity of the nonlinear structure. Note that if the ratio \(v_{d}^{\ast }\) equals the nonlinear velocity, u, in Eq. (9), then the above solution ceases to exist.

5 Results and discussion

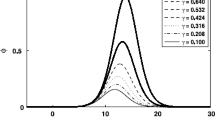
We have numerically investigated the dependence of nonlinear dispersive dust drift shock waves on the non-Maxwellian population of ions (both Cairns and Kappa distributed), collisional frequency, and the inverse dust inhomogeneity scale length. It is observed that the system under consideration admits compressive shocks unlike the electron-ion (e-i) case where rarefactive shocks are obtained owing to the negative charge of the dust as opposed to the positive ions in the e-i case. Moreover, it is found that unlike the acoustic waves in a homogeneous plasma case (Cairns et al. 1995), the drift shock wave never turns into a rarefactive shock for any set of plasma parameters. Figure 2a shows the graphical representation of the compressive dust drift shock potential obtained by varying the non-Maxwellian. population of ions for the Cairns distribution. It is observed that the increasing the non-Maxwellian. population of the Cairns distributed ions mitigates the dust drift shock wave. Figure 2b explores the same for the Kappa distributed ions. It is observed that as opposed to the Cairns distributed ions, the Kappa distributed ions enhance the dust drift shock wave. This is due to the difference of shapes of both the distribution functions which eventually result into the difference in the density expressions which we know is the zero order moment of the distribution function. The top grey shock wave in both Figs. 2a and 2b represents the case when the ions are considered Maxwellian. It is evident that for both the Cairns and Kappa distributed electrons the strength of the dust drift shock wave is weaker by comparison with the Maxwellian distributed ions.

Fig. 2
figure 2

Variation of the electrostatic drift potential Φ with non-Maxwellian. ion population parameters α (a) and κ (b). Other parameters are κ nd =0.01,ν nd /Ω d =0.01,n e0/n i0=0.1 and T i /T e =0.01

Full size image

Figure 3a exhibits the effect of increasing dust neutral collision frequency on the structure of dust drift shock waves when the Cairns distributed ions are taken. It is observed that the increasing dust neutral collisional frequency enhances the shock strength of the nonlinear dust drift waves. This is due to the fact that the increase in the collision frequency is tantamount to increasing the dissipation and hence the observed increase in the shock wave results. The similar trend is obtained for Kappa distributed ions as shown in Fig. 3b.

Fig. 3
figure 3

Variation of the electrostatic drift potential Φ with decreasing dust-neutral collision frequency i.e. ν nd for Cairns distributed ions (a) and for Kappa distributed ions (b). Other parameters are κ nd =0.01,α=0.1,κ=2,n e0/n i0=0.1 and T i /T e =0.01

Full size image

Finally, Figs. 4a and 4b explore the effect of increasing inverse density inhomogeneity scale length, κ nd , on the nonlinear dust drift shock wave with both Cairns and Kappa distributed ions respectively. It is found that the increasing κ nd decreases the shock strength in both the cases. This is due to the dependence of nonlinear velocity of the shock structure on the diamagnetic drift velocity which in turn is a function of κ nd . It is worth mentioning that the non-Maxwellian ion population modifies the expression for T eff which in turn changes the acoustic speed and the Larmor radius, consequently, changing the scale lengths over which the nonlinear structures are formed.

Fig. 4
figure 4

Variation of the electrostatic shock potential Φ with inverse density inhomogeneity scale length, i.e. κ nd for Cairns distributed ions (a) and for Kappa distributed ions (b). Other parameters are ν nd /Ω d =0.01,α=0.1,κ=2,n e0/n i0=0.1 and T i /T e =0.01

Full size image

6 Conclusion

In this paper, we have investigated the nonlinear propagation characteristics of the dust drift shock waves in the presence of Maxwellian, Cairns, and Kappa distributed ions whereas the electrons have been assumed to follow the Boltzmann’s distribution throughout. The linear dispersion relation for the system under consideration has also been derived and it has been shown that the frequency of the dust drift wave is greatest for the Cairns, intermediate for Kappa and the least for the Maxwellian distributed ions. Using the drift approximation, a nonlinear equation has been derived for the dust drift shock waves which reduces to a KdVB-like equation in the comoving frame of reference. The solution of the KdVB-like equation has been obtained using the tanh method. It has been found that the non-Maxwellian ion population, dust neutral collision frequency as well as the inverse dust density scale length inhomogeneity alter the propagation characteristics of the nonlinear dust drift shock waves. It has been found that the drift shock strength is weaker for non-Maxwellian population of ions by comparison with the Maxwellian population. Most importantly, it has been found that the non-Maxwellian distribution alters the scale lengths over which the nonlinear structures are formed. The present investigation may have relevance to understand the nonlinear propagation of shock waves in inhomogeneous plasmas with non-Maxwellian population of ions such as those found in the planetary magnetospheres.