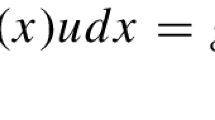Skip to main content
SpringerLink
Log in

Long-time behavior of small solutions to quasilinear dissipative hyperbolic equations

  • Published:
Applications of Mathematics Aims and scope Submit manuscript

Abstract

We give sufficient conditions for the existence of global small solutions to the quasilinear dissipative hyperbolic equation

$u_{tt} + 2u_t - a_{ij} (u_t ,\nabla u)\partial _i \partial _j u = f$

corresponding to initial values and source terms of sufficiently small size, as well as of small solutions to the corresponding stationary version, i.e. the quasilinear elliptic equation

$ - a_{ij} (0,\nabla v)\partial _i \partial _j v = h$

. We then give conditions for the convergence, as t → ∞, of the solution of the evolution equation to its stationary state.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. Adams, J. Fournier: Sobolev Spaces, 2nd ed. Academic Press, New York, 2003.

    MATH  Google Scholar 

  2. C. Cattaneo: Sulla Conduzione del Calore. Atti Semin. Mat. Fis., Univ. Modena 3 (1949), 83–101. (In Italian.)

    MathSciNet  MATH  Google Scholar 

  3. KP. Hadeler: Random walk systems and reaction telegraph equations. In: Dynamical Systems and their Applications (S. van Strien, S.V. Lunel, eds.). Royal Academy of the Netherlands, 1995.

  4. H.A. Haus: Waves and Fields in Optoelectronics. Prentice Hall, 1984.

  5. T. Kato: Abstract Differential Equations and Nonlinear Mixed Problems. Fermian Lectures. Academie Nazionale dei Licei, Pisa, 1985.

    Google Scholar 

  6. S. Klainerman: Global existence for nonlinear wave equations. Commun. Pure Appl. Math. 33 (1980), 43–101.

    Article  MathSciNet  MATH  Google Scholar 

  7. Ta-Tsien Li: Nonlinear Heat Conduction with Finite Speed of Popagation. Proceedings of the China-Japan Symposium on Reaction Diffusion Equations and their Applcations to Computational Aspects. World Scientific, Singapore, 1997.

    Google Scholar 

  8. A. Matsumura: On the asymptotic behavior of solutions to semi-linear wave equations. Publ. Res. Inst. Mat. Sci., Kyoto Univ. 12 (1976), 169–189.

    Article  MathSciNet  MATH  Google Scholar 

  9. A. Matsumura: Global existence and asymptotics of the solutions of second-order quasilinear hyperbolic equations with first-order dissipation. Publ. Res. Inst. Mat. Sci., Kyoto Univ. 13 (1977), 349–379.

    Article  MathSciNet  MATH  Google Scholar 

  10. A. Milani: The quasi-stationary Maxwell equations as singular limit of the complete equations: The quasi-linear case. J. Math. Anal. Appl. 102 (1984), 251–274.

    Article  MathSciNet  MATH  Google Scholar 

  11. A. Milani: Global existence via singular perturbations for quasilinear evolution equations. Adv. Math. Sci. Appl. 6 (1996), 419–444.

    MathSciNet  MATH  Google Scholar 

  12. S. Mizohata: The Theory of Partial Differential Equations. Cambridge University Press, London, 1973.

    MATH  Google Scholar 

  13. J. Moser: A rapidly convergent iteration method and non-linear differential equations. Ann. Sc. Norm. Super. Pisa, Sci. Fis. Mat., III. Ser. 20 (1966), 265–315.

    Google Scholar 

  14. G. Ponce: Global existence of small solutions to a class of nonlinear evolution equations. Nonlin. Anal., Theory Methods Appl. 9 (1985), 399–418.

    Article  MathSciNet  MATH  Google Scholar 

  15. R. Racke: Non-homogeneous nonlinear damped wave equations in unbounded domains. Math. Methods Appl. Sci. 13 (1990), 481–491.

    Article  MathSciNet  MATH  Google Scholar 

  16. R. Racke: Lectures on Nonlinear Evolution Equations. Initial Value Problems. Vieweg, Braunschweig, 1992.

    MATH  Google Scholar 

  17. S. Schochet: The instant-response limit in Whitham’s nonlinear traffic flow model: Uniform well-posedness and global existence. Asymptotic Anal. 1 (1988), 263–282.

    MathSciNet  MATH  Google Scholar 

  18. H. Yang, A. Milani: On the diffusion phenomenon of quasilinear hyperbolic waves. Bull. Sci. Math. 124 (2000), 415–433.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Milwaukee, USA

    Albert Milani & Hans Volkmer

  2. Department of Mathematics, University of Wisconsin, P.O.Box 413, Milwaukee, WI, 53201, USA

    Albert Milani

Authors
  1. Albert Milani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hans Volkmer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Albert Milani.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Milani, A., Volkmer, H. Long-time behavior of small solutions to quasilinear dissipative hyperbolic equations. Appl Math 56, 425–457 (2011). https://doi.org/10.1007/s10492-011-0025-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10492-011-0025-0

Keywords

MSC 2010

Search

Navigation