Skip to main content
SpringerLink
Log in

An ensemble discrete water wave optimization algorithm for the blocking flow-shop scheduling problem with makespan criterion

  • Published:
Applied Intelligence Aims and scope Submit manuscript

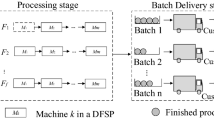
Abstract

Production scheduling plays a pivotal role in smart factories due to the development of intelligent manufacturing. As a typical scheduling problem, the blocking flow-shop scheduling problem (BFSP) has attracted enormous attention from researchers. In this paper, an ensemble discrete water wave optimization algorithm (EDWWO) is proposed with the criterion to minimize the makespan. In the proposed algorithm, a constructive heuristic is presented to suit the needs of initial solutions quality. The constructive heuristic is based on a new dispatching rule combined with the well-known NEH heuristic. The algorithmic characteristics are explored and effective technologies, such as data-driven mechanism in the propagation phase, a block-shifting operator based on the framework of the variable neighborhood search in the breaking phase, and perturbation strategy, are employed to improve the performance of the algorithm. The effectiveness of operators and parameters in EDWWO are analyzed and calibrated based on the design of experiments. To evaluate the algorithmic performance, the well-known benchmark problem is adopted for comparison with five other state-of-the-art algorithms. Meanwhile, the statistical validity of the results is investigated by introducing the Friedman-test and Wilcoxon-test. The statistical results demonstrate the effectiveness of EDWWO for solving the BFSP.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Wikarek J, Sitek P (2021) Proactive and reactive approach to employee competence configuration problem in planning and scheduling processes. Appl Intell 2021:1–20. https://doi.org/10.1007/S10489-021-02594-X

    Article  Google Scholar 

  2. Ivanov D, Dolgui A, Sokolov B et al (2016) A dynamic model and an algorithm for short-term supply chain scheduling in the smart factory industry 4.0. Int J Prod Res 54:386–402. https://doi.org/10.1080/00207543.2014.999958

    Article  Google Scholar 

  3. Zhou G, Zhou Y, Zhao R (2021) Hybrid Social Spider Optimization Algorithm with Differential Mutation Operator for the Job-Shop Scheduling Problem. J Ind Manag Optim 17:533–548. https://doi.org/10.3934/JIMO.2019122

    Article  MathSciNet  MATH  Google Scholar 

  4. Wan J, Chen B, Wang S et al (2018) Fog Computing for Energy-Aware Load Balancing and Scheduling in Smart Factory. IEEE Trans Ind Informatics 14:4548–4556. https://doi.org/10.1109/TII.2018.2818932

    Article  Google Scholar 

  5. Fang CJ, Wang L, Ping PZ (2019) A collaborative optimization algorithm for energy-efficient multi-objective distributed no-idle flow-shop scheduling. Swarm Evol Comput:50. https://doi.org/10.1016/J.SWEVO.2019.100557

  6. Zhao F, Ma R, Wang L (2021) A Self-Learning Discrete Jaya Algorithm for Multiobjective Energy-Efficient Distributed No-Idle Flow-Shop Scheduling Problem in Heterogeneous Factory System. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2021.3086181

  7. Lu C, Huang Y, Meng L et al (2022) A Pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers. Robot Comput Integr Manuf 74:102277. https://doi.org/10.1016/J.RCIM.2021.102277

    Article  Google Scholar 

  8. Shao Z, Shao W, Pi D (2020) Effective Constructive Heuristic and Metaheuristic for the Distributed Assembly Blocking Flow-shop Scheduling Problem. Appl Intell 50(12):4647–4669. https://doi.org/10.1007/S10489-020-01809-X

    Article  Google Scholar 

  9. Hamzadayı A, Arvas MA, Elmi A (2021) Distributed assembly permutation flow shop problem; Single seekers society algorithm. J Manuf Syst 61:613–631. https://doi.org/10.1016/J.JMSY.2021.10.012

    Article  Google Scholar 

  10. Chen S, Pan QK, Gao L (2021) Production scheduling for blocking flowshop in distributed environment using effective heuristics and iterated greedy algorithm. Robot Comput Integr Manuf:71. https://doi.org/10.1016/J.RCIM.2021.102155

  11. Zhao F, He X, Wang L (2020) A Two-Stage Cooperative Evolutionary Algorithm With Problem-Specific Knowledge for Energy-Efficient Scheduling of No-Wait Flow-Shop Problem. IEEE Trans Cybern:1–13. https://doi.org/10.1109/tcyb.2020.3025662

  12. Rossi FL, Nagano MS (2021) Heuristics and iterated greedy algorithms for the distributed mixed no-idle flowshop with sequence-dependent setup times. Comput Ind Eng:157. https://doi.org/10.1016/J.CIE.2021.107337

  13. Shao Z, Pi D, Shao W (2019) A novel multi-objective discrete water wave optimization for solving multi-objective blocking flow-shop scheduling problem. Knowledge-Based Syst 165:110–131. https://doi.org/10.1016/j.knosys.2018.11.021

    Article  Google Scholar 

  14. Chen Q, Pan Q, Zhang B, et al. (2019) Algorithms in Compact Strip Production 16:1933–1951

  15. Merchan AF, Maravelias CT (2016) Preprocessing and tightening methods for time-indexed MIP chemical production scheduling models. Comput Chem Eng 84:516–535. https://doi.org/10.1016/J.COMPCHEMENG.2015.10.003

    Article  Google Scholar 

  16. Riahi V, Khorramizadeh M, Newton MAH, Sattar A (2017) Scatter search for mixed blocking flowshop scheduling. Expert Syst Appl 79:20–32. https://doi.org/10.1016/j.eswa.2017.02.027

    Article  Google Scholar 

  17. Miyata HH, Nagano MS (2019) The blocking flow shop scheduling problem: A comprehensive and conceptual review. Expert Syst. Appl. 137:130–156

    Article  Google Scholar 

  18. Zhao F, Xue F, Zhang Y et al (2019) A discrete gravitational search algorithm for the blocking flow shop problem with total flow time minimization. Appl Intell 499(49):3362–3382. https://doi.org/10.1007/S10489-019-01457-W

    Article  Google Scholar 

  19. He X, Pan Q, Gao L et al (2021) A Greedy Cooperative Co-evolution ary Algorithm with Problem-specific Knowledge for Multi-objective Flowshop Group Scheduling Problems. IEEE Trans Evol Comput:1–1. https://doi.org/10.1109/TEVC.2021.3115795

  20. Nawaz M, Enscore EE, Ham I (1983) A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 11:91–95. https://doi.org/10.1016/0305-0483(83)90088-9

    Article  Google Scholar 

  21. McCormick ST, Pinedo ML, Shenker S, Wolf B (1989) Sequencing in an assembly line with blocking to minimize cycle time. Oper Res 37:925–935. https://doi.org/10.1287/OPRE.37.6.925

    Article  MATH  Google Scholar 

  22. Wang L, Pan QK, Suganthan PN et al (2010) A novel hybrid discrete differential evolution algorithm for blocking flow shop scheduling problems. Comput Oper Res 37:509–520. https://doi.org/10.1016/j.cor.2008.12.004

    Article  MathSciNet  MATH  Google Scholar 

  23. Liang JJ, Pan QK, Tiejun C, Wang L (2011) Solving the blocking flow shop scheduling problem by a dynamic multi-swarm particle swarm optimizer. Int J Adv Manuf Technol 55:755–762. https://doi.org/10.1007/S00170-010-3111-7

    Article  Google Scholar 

  24. Wang L, Pan QK, Tasgetiren MF (2011) A hybrid harmony search algorithm for the blocking permutation flow shop scheduling problem. Comput Ind Eng 61:76–83. https://doi.org/10.1016/J.CIE.2011.02.013

    Article  Google Scholar 

  25. Han YY, Gong D, Sun X (2015) A discrete artificial bee colony algorithm incorporating differential evolution for the flow-shop scheduling problem with blocking. Eng Optim 47:927–946. https://doi.org/10.1080/0305215X.2014.928817

    Article  MathSciNet  Google Scholar 

  26. Han Y, Gong D, Li J, Zhang Y (2016) Solving the blocking flow shop scheduling problem with makespan using a modified fruit fly optimisation algorithm. Int J Prod Res 54:6782–6797. https://doi.org/10.1080/00207543.2016.1177671

    Article  Google Scholar 

  27. Eddaly M, Jarboui B, Siarry P (2016) Combinatorial particle swarm optimization for solving blocking flowshop scheduling problem. J Comput Des Eng 3:295–311. https://doi.org/10.1016/j.jcde.2016.05.001

    Article  Google Scholar 

  28. Shao Z, Pi D, Shao W (2018) Estimation of distribution algorithm with path relinking for the blocking flow-shop scheduling problem. Eng Optim 50:894–916. https://doi.org/10.1080/0305215X.2017.1353090

    Article  MathSciNet  Google Scholar 

  29. Shao Z, Pi D, Shao W (2018) A multi-objective discrete invasive weed optimization for multi-objective blocking flow-shop scheduling problem. Expert Syst Appl 113:77–99. https://doi.org/10.1016/j.eswa.2018.06.020

    Article  Google Scholar 

  30. Abu Doush I, Al-Betar MA, Awadallah MA et al (2019) Flow shop scheduling with blocking using modified harmony search algorithm with neighboring heuristics methods. Appl Soft Comput J. https://doi.org/10.1016/J.ASOC.2019.105861

  31. Shao Z, Pi D, Shao W (2017) Self-adaptive discrete invasive weed optimization for the blocking flow-shop scheduling problem to minimize total tardiness. Comput Ind Eng 111:331–351. https://doi.org/10.1016/j.cie.2017.07.037

    Article  Google Scholar 

  32. Shao Z, Pi D, Shao W (2018) A novel discrete water wave optimization algorithm for blocking flow-shop scheduling problem with sequence-dependent setup times. Swarm Evol Comput 40:53–75. https://doi.org/10.1016/j.swevo.2017.12.005

    Article  Google Scholar 

  33. Han Y, Li J, Sang H et al (2020) Discrete evolutionary multi-objective optimization for energy-efficient blocking flow shop scheduling with setup time. Appl Soft Comput J 93. https://doi.org/10.1016/J.ASOC.2020.106343

  34. Ribas I, Companys R, Tort-Martorell X (2017) Efficient heuristics for the parallel blocking flow shop scheduling problem. Expert Syst Appl 74:41–54. https://doi.org/10.1016/j.eswa.2017.01.006

    Article  Google Scholar 

  35. Ribas I, Companys R, Tort-Martorell X (2019) An iterated greedy algorithm for solving the total tardiness parallel blocking flow shop scheduling problem. Expert Syst Appl 121:347–361. https://doi.org/10.1016/j.eswa.2018.12.039

    Article  Google Scholar 

  36. Shao Z, Pi D, Shao W (2020) Hybrid enhanced discrete fruit fly optimization algorithm for scheduling blocking flow-shop in distributed environment. Expert Syst Appl 145:113147. https://doi.org/10.1016/j.eswa.2019.113147

    Article  Google Scholar 

  37. Shao Z, Shao W, Pi D (2020) Effective heuristics and metaheuristics for the distributed fuzzy blocking flow-shop scheduling problem. Swarm Evol Comput:59. https://doi.org/10.1016/J.SWEVO.2020.100747

  38. Shao Z, Shao W, Pi D (2021) Effective constructive heuristic and iterated greedy algorithm for distributed mixed blocking permutation flow-shop scheduling problem. Knowledge-Based Syst:221. https://doi.org/10.1016/J.KNOSYS.2021.106959

  39. Ribas I, Companys R (2021) A computational evaluation of constructive heuristics for the parallel blocking flow shop problem with sequence-dependent setup times. Int J Ind Eng Comput 12:321–328. https://doi.org/10.5267/J.IJIEC.2021.1.004

    Article  Google Scholar 

  40. Ribas I, Companys R, Tort-Martorell X (2021) An iterated greedy algorithm for the parallel blocking flow shop scheduling problem and sequence-dependent setup times. Expert Syst Appl:184. https://doi.org/10.1016/J.ESWA.2021.115535

  41. Zhao F, Zhao L, Wang L, Song H (2020) An ensemble discrete differential evolution for the distributed blocking flowshop scheduling with minimizing makespan criterion. Expert Syst Appl 160:113678. https://doi.org/10.1016/j.eswa.2020.113678

    Article  Google Scholar 

  42. Li YY, Lin J, Wang ZJ (2021) Multi-skill resource constrained project scheduling using a multi-objective discrete Jaya algorithm. Appl Intell. https://doi.org/10.1007/S10489-021-02608-8

  43. Tasgetiren MF, Kizilay D, Pan QK, Suganthan PN (2017) Iterated greedy algorithms for the blocking flowshop scheduling problem with makespan criterion. Comput Oper Res 77:111–126. https://doi.org/10.1016/j.cor.2016.07.002

    Article  MathSciNet  MATH  Google Scholar 

  44. Sang H, Pan Q, Li J et al (2019) Effective invasive weed optimization algorithms for distributed assembly permutation flowshop problem with total flowtime criterion. Swarm Evol Comput 44:64–73. https://doi.org/10.1016/j.swevo.2018.12.001

    Article  Google Scholar 

  45. Zhou Y, Zhang J, Yang X, Ling Y (2019) Optimization of PID controller based on water wave optimization for an automatic voltage regulator system. Inf Technol Control 48:160–171. https://doi.org/10.5755/J01.ITC.48.1.20296

    Article  Google Scholar 

  46. Zheng Y (2015) Water wave optimization: A new nature-inspired metaheuristic. Comput Oper Res 55:1–11. https://doi.org/10.1016/j.cor.2014.10.008

    Article  MathSciNet  MATH  Google Scholar 

  47. Zhang J, Zhou Y, Luo Q (2018) An improved sine cosine water wave optimization algorithm for global optimization. J Intell Fuzzy Syst 34:2129–2141. https://doi.org/10.3233/JIFS-171001

    Article  Google Scholar 

  48. Zhang J, Zhou Y, Luo Q (2019) Nature-inspired approach: a wind-driven water wave optimization algorithm. Appl Intell 49:233–252. https://doi.org/10.1007/S10489-018-1265-4

    Article  Google Scholar 

  49. Medara R, Singh RS, Amit (2021) Energy-aware workflow task scheduling in clouds with virtual machine consolidation using discrete water wave optimization. Simul Model Pract Theory 110:102323. https://doi.org/10.1016/j.simpat.2021.102323

    Article  Google Scholar 

  50. Yan Z, Zhang J, Tang J (2021) Path planning for autonomous underwater vehicle based on an enhanced water wave optimization algorithm. Math Comput Simul 181:192–241. https://doi.org/10.1016/j.matcom.2020.09.019

    Article  MathSciNet  MATH  Google Scholar 

  51. Lu XQ, Yan HF, Su ZL et al (2021) Metaheuristics for homogeneous and heterogeneous machine utilization planning under reliability-centered maintenance. Comput Ind Eng 151:106934. https://doi.org/10.1016/j.cie.2020.106934

    Article  Google Scholar 

  52. Zhou Y, Zhang J, Yang X, Ling Y (2020) Optimal reactive power dispatch using water wave optimization algorithm. Oper Res 20:2537–2553. https://doi.org/10.1007/S12351-018-0420-3

    Article  Google Scholar 

  53. Yun X, Feng X, Lyu X et al (2016) A novel water wave optimization based memetic algorithm for flow-shop scheduling. IEEE Congr Evol Comput 2016:1971–1976

  54. Zhao F, Liu H, Zhang Y et al (2018) A discrete Water Wave Optimization algorithm for no-wait flow shop scheduling problem. Expert Syst Appl 91:347–363. https://doi.org/10.1016/j.eswa.2017.09.028

    Article  Google Scholar 

  55. Zhao F, Zhang L, Zhang Y et al (2020) A hybrid discrete water wave optimization algorithm for the no-idle flowshop scheduling problem with total tardiness criterion. Expert Syst Appl 146. https://doi.org/10.1016/j.eswa.2019.113166

  56. Zhao F, Zhang L, Cao J, Tang J (2021) A cooperative water wave optimization algorithm with reinforcement learning for the distributed assembly no-idle flowshop scheduling problem. Comput Ind Eng 153:107082. https://doi.org/10.1016/j.cie.2020.107082

    Article  Google Scholar 

  57. Zhao F, Zhang L, Liu H et al (2019) An improved water wave optimization algorithm with the single wave mechanism for the no-wait flow-shop scheduling problem. Eng Optim 51:1727–1742. https://doi.org/10.1080/0305215X.2018.1542693

    Article  MathSciNet  Google Scholar 

  58. Lawler EL, Lenstra JK, Rinnooy Kan AHG (1982) Recent Developments in Deterministic Sequencing and Scheduling: A Survey. Determ Stoch Sched:35–73. https://doi.org/10.1007/978-94-009-7801-0_3

  59. Bhatt KC, Malav PK, Gore PG et al (2021) A note on distribution and potential of Japanese wild adzuki bean [Vigna angularis var. nipponensis (Ohwi) Ohwi and H. Ohashi] in India. Genet Resour Crop Evol 68:2157–2166. https://doi.org/10.1007/s10722-021-01130-7

    Article  Google Scholar 

  60. Zhao F, Zhao J, Wang L, Tang J (2021) An optimal block knowledge driven backtracking search algorithm for distributed assembly No-wait flow shop scheduling problem. Appl Soft Comput 112:107750. https://doi.org/10.1016/j.asoc.2021.107750

    Article  Google Scholar 

  61. Ding JY, Song S, Zhang R et al (2015) A novel Block-shifting simulated annealing algorithm for the no-wait flowshop scheduling problem. IEEE Congr Evol Comput 2015:2768–2774. https://doi.org/10.1109/CEC.2015.7257232

    Article  Google Scholar 

  62. Rossi FL, Nagano MS (2020) Heuristics and metaheuristics for the mixed no-idle flowshop with sequence-dependent setup times and total tardiness minimisation. Swarm Evol Comput 55:100689. https://doi.org/10.1016/j.swevo.2020.100689

    Article  Google Scholar 

  63. Khare A, Agrawal S (2020) Effective heuristics and metaheuristics to minimise total tardiness for the distributed permutation flowshop scheduling problem. Int J Prod Res 0:1–17. https://doi.org/10.1080/00207543.2020.1837982

    Article  Google Scholar 

  64. Smith JR, Larson C (2019) Statistical approaches in surface finishing. Part 3. Design-of-experiments. Trans Inst Met Finish 97:289–294. https://doi.org/10.1080/00202967.2019.1673530

    Article  Google Scholar 

  65. Jaeger TF (2008) Categorical data analysis: Away from ANOVAs (transformation or not) and towards logit mixed models. J Mem Lang 59:434–446. https://doi.org/10.1016/j.jml.2007.11.007

    Article  Google Scholar 

  66. Pan QK, Gao L, Xin-Yu L, Framinan JM (2019) Effective constructive heuristics and meta-heuristics for the distributed assembly permutation flowshop scheduling problem. Appl Soft Comput 81:105492. https://doi.org/10.1016/j.asoc.2019.105492

    Article  Google Scholar 

  67. Zhang G, Xing K, Cao F (2018) Discrete differential evolution algorithm for distributed blocking flowshop scheduling with makespan criterion. Eng Appl Artif Intell 76:96–107. https://doi.org/10.1016/j.engappai.2018.09.005

    Article  Google Scholar 

  68. Ying KC, Lin SW, Cheng CY, He CD (2017) Iterated reference greedy algorithm for solving distributed no-idle permutation flowshop scheduling problems. Comput Ind Eng 110:413–423. https://doi.org/10.1016/j.cie.2017.06.025

    Article  Google Scholar 

  69. Ruiz R, Pan QK, Naderi B (2019) Iterated Greedy methods for the distributed permutation flowshop scheduling problem. Omega (United Kingdom) 83:213–222. https://doi.org/10.1016/j.omega.2018.03.004

    Article  Google Scholar 

  70. Ribas I, Companys R, Tort-Martorell X (2017) Efficient heuristics for the parallel blocking flow shop scheduling problem. Expert Syst Appl 74:41–54. https://doi.org/10.1016/j.eswa.2017.01.006

    Article  Google Scholar 

  71. Naderi B, Ruiz R (2014) A scatter search algorithm for the distributed permutation flowshop scheduling problem. Eur J Oper Res 239:323–334. https://doi.org/10.1016/j.ejor.2014.05.024

    Article  MathSciNet  MATH  Google Scholar 

  72. Garcia S, Molina D, Lozano M, Herrera F (2009) A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: a case study on the CEC’2005 Special Session on Real Parameter Optimization. J Heuristics 15:617–644. https://doi.org/10.1007/s10732-008-9080-4

    Article  MATH  Google Scholar 

Download references

Funding

This work was financially supported by the National Natural Science Foundation of China under grant 62063021. It was also supported by the Key talent project of Gansu Province (ZZ2021G50700016), the Key Research Programs of Science and Technology Commission Foundation of Gansu Province (21YF5WA086), Lanzhou Science Bureau project (2018-rc-98), and Project of Gansu Natural Science Foundation (21JR7RA204), respectively.

Author information

Authors and Affiliations

  1. School of Computer and Communication, Lanzhou University of Technology, Lanzhou, 730050, China

    Fuqing Zhao, Dongqu Shao, Tianpeng Xu & Ningning Zhu

  2. Department of Industrial Engineering, Universitas Andalas, Padang, 25163, Indonesia

    Jonrinaldi

Authors
  1. Fuqing Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dongqu Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tianpeng Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ningning Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jonrinaldi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fuqing Zhao.

Ethics declarations

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Conflict of interest

All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript.

Informed Consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, F., Shao, D., Xu, T. et al. An ensemble discrete water wave optimization algorithm for the blocking flow-shop scheduling problem with makespan criterion. Appl Intell 52, 15824–15843 (2022). https://doi.org/10.1007/s10489-022-03236-6

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-022-03236-6

Keywords

Search

Navigation