1 Introduction

Methods for handling uncertainty have been extensively studied for many real world applications such as approximate reasoning and decision making. The first and key step is to reasonably describe and model the uncertain information. One of the most common theories is Dempster-Shafer evidence theory, which is also called Dempster-Shafer theory or evidence theory. Since it was first proposed by Dempster [6] and then developed by Shafer [46], it has continually attracted an increasing amount of interest [2–4, 7, 8, 13, 15, 16, 19–21, 23, 27, 29–31, 34, 36–39, 41, 50, 52, 53, 55–58, 60, 63].

One open issue in evidence theory is conflict management when evidence is highly conflicting. A famous example was illustrated by Zadeh [62]. Since then, hundreds of methods have been proposed to address this issue [14, 17, 25, 32, 33, 35, 40, 42, 44, 45, 59, 61]. The Dempster combination rule is important to Dempster-Shafer theory, but, in its classical form, it is incapable of dealing with highly conflicting evidence.

Many researchers have investigated the Dempster combination rule and conflict management. Yager [54] pointed out that the normalization step in Dempster combination rule is questionable, and that it should be deleted so as to assign the conflict to the whole set under the closed-world assumption where the frame of discernment is exhaustive. The transferable belief model (TBM) [47, 48] was proposed to represent quantified beliefs based on belief functions. TBM was constructed using two levels: the credal level, where beliefs are entertained and quantified by belief functions; and the pignistic level, where beliefs can be used to make decisions and are quantified by probability functions. Compared with Yager’s rule of combination that concerns the assignment of the conflicting mass, Dubois and Prade [22] proposed a new combination rule that is more adaptable and specific. Lefevre et al. [33] reviewed existing work and proposed a unified model for handling conflicting evidence. They noted that the main idea behind previous methods was to determine which hypothesis the conflict will be assigned to, and how it will be assigned.

Essentially, the idea of assigning the conflict to different hypotheses has changed Dempster combination rule, which was questioned by Haenni [24]. When a model X with method Y leads to a counter-intuitive result Z, Haenni argued that is not appropriate to modify method Y, because a counter-intuitive result may be caused by model X. Some methods coincide with Haenni’s opinion. For example, Murphy [40] averaged the conflict evidence and then combined the averaged evidence itself several times. A weighted average method was proposed by Deng et al. [14], which had a better convergence rate. In the weighted average method, the evidence distance function presented in [28] (instead of the commonly used conflict coefficient in evidence theory) was used to model the conflict degree. Moreover, Liu [35] noted that the commonly used conflict coefficient in evidence theory is not appropriate for representing the degree of conflict between two pieces of evidence. To address this issue, we propose a two dimensional conflict measure, which is combined with the classical conflict coefficient and the pignistic betting distance. We also investigated the applicability of Dempster combination rule, and the present three cases according to the two-dimensional conflict measure.

Although various methods have been proposed by either introducing new combination operators or modifying the data models, there is lack of systemic and comprehensive analyses and explanations on the origin of conflict in conflict management. Conflict management can only be effectively conducted if it is based on reasonable explanations on the cause of conflict. Based on this, we propose a novel theory called generalized evidence theory (GET). GET concludes that there are two main causes for evidence conflicts. One is questionable sensor reliability caused by disturbances or the condition of equipment. The other is that the system is in open world where our knowledge is not complete. In contrast with a closed world, open world means that the frame of discernment in traditional Dempster-Shafer theory is incomplete. GET provides the generalized basic probability assignment (GBPA) concept for data expression and modeling. It also provides a generalized combination rule (GCR) for combining conflicting or inconsistent evidence, and a new conflict model. Based on this new concept, rule, and model, GET actually generalizes traditional Dempster-Shafer theory. In other words, Dempster-Shafer theory becomes a special case of GET. We have used many numerical examples to demonstrate the effectiveness and appropriateness of the proposed GET.

The remainder of this paper is organized as follows. In Section 2, we briefly introduce some background knowledge, including Dempster-Shafer theory [6, 46], the pignistic probability transformation [49], Jousselme’s evidence distance [28], and Liu’s evidence conflict model [35]. In Section 3, we present GET, the generalized evidence distance, the GCR, and their applications. We discuss the ∅ generalized conflict model and its application in Section 4. Finally, our conclusions are given in Section 5.

2 Preliminaries

2.1 Dempster-Shafer theory

For completeness, we introduce the following basic concepts of Dempster-Shafer theory [6, 46].

For a finite nonempty set Ω={H 1,H 2,⋯,H N }, Ω is called a frame of discernment when it satisfies

$$ H_{i} \cap H_{j} = \emptyset , \quad \forall i,j = \{ 1, \cdots, N\}. $$
(1)

Let 2Ω be the set of all subsets of Ω, namely

$$ 2^{\Omega} = \{ A \;\; | \;\; A \subseteq {\Omega} \}. $$
(2)

2Ω is called the power set of Ω. For FOD Ω, a mass function is a mapping m from 2Ω to [0,1], formally defined as

$$ m: \quad 2^{\Omega} \to [0,1], $$
(3)

which satisfies the condition

$$\begin{array}{@{}rcl@{}} \sum\limits_{A \in {2^{\Omega} }} {m(A) = 1} \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} m(\emptyset ) = 0. \end{array} $$
(5)

In Dempster-Shafer theory, a mass function is also called a basic probability assignment (BPA). Given a BPA, the belief function B e l : 2Ω→[0,1] is defined as

$$ Bel(A) = \sum\limits_{B \subseteq A} {m(B)}. $$
(6)

The plausibility function P l : 2Ω→[0,1] is defined as

$$ Pl(A) = 1 - Bel(\bar A) = \sum\limits_{B \cap A \ne \emptyset } {m(B)}, $$
(7)

where \(\bar A = {\Omega } - A\). The functions B e l and P l express the lower and upper bounds of the support of subset A, respectively.

Dempster combination rule (denoted by m=m 1⊕m 2) is used to combine two independent BPAs (m 1 and m 2). It is defined as

$$ m(A) = \left\{ \begin{array}{l} \frac{1}{{1 - K}}\sum\limits_{A = B \cap C} {m_{1} (B)m_{2} (C)} ,\quad A \ne \emptyset ; \\ 0,\quad \quad \quad \quad \quad \quad \qquad \quad \qquad \quad A = \emptyset . \\ \end{array} \right. $$
(8)

where

$$ K = \sum\limits_{B \cap C = \emptyset } {m_{1} (B) \cdot m_{2} (C)}. $$
(9)

Note that Dempster combination rule is only applicable to two BPAs that satisfy K<1.

2.2 Pignistic probability transformation

In the transferable belief model (TBM) [47], pignistic probabilities are typically used to make decisions.

Let m be a BPA on the frame of discernment Ω. Its associated pignistic probability transformation (PPT), B e t P m :Ω→[0,1], is defined as

$$ BetP_{m} (\omega) \,=\, \sum\limits_{A \subseteq P({\Omega} ),\omega \in A} {\frac{1}{{|A|}}} \frac{{m(A)}}{{1 - m(\emptyset )}},\quad m(\emptyset ) \ne 1, $$
(10)

where |A| is the cardinality of subset A. The PPT process transforms basic probability assignments to probability distributions. Therefore, the pignistic betting distance [49] can be easily obtained using the PPT.

Let m 1 and m 2 be two BPAs on the frame of discernment Ω. Then, the pignistic probability transformations are \(BetP_{m_{1}}\) and \(BetP_{m_{2}}\). The pignistic betting distance, \({d{\kern -.5pt}i{}f{\kern -2.5pt}BetP}_{{m_{1}}}^{{m_{2}}}\) (d i f B e t P for short), between \(BetP_{m_{1}}\) and \(BetP_{m_{2}}\) is

$$ {d{\kern-.5pt}i{}f{\kern-2.5pt}BetP} = {\max\limits_{A \subseteq {\Omega} }}(\left| {Bet{P_{{m_{1}}}}(A) - Bet{P_{{m_{2}}}}(A)} \right|) $$
(11)

\(\left | {Bet{P_{{m_{1}}}}(A) - Bet{P_{{m_{2}}}}(A)} \right |\) indicates the support degree of the BPAs.

2.3 Jousselme’s evidence distance

Jousselme et al. [28] proposed a new distance measure for the conflict between two bodies of evidence, which is also called the evidence distance.

Let m 1 and m 2 be two BPAs defined on the same frame of discernment, Ω, which contain N mutually exclusive and exhaustive hypotheses. Let d B P A (m 1,m 2) represent the distance between two bodies of evidence, defined as

$$ d_{BPA} (m_{1} ,m_{2} ) = \sqrt {\frac{1}{2}\left( {{m_{1} } - {m_{2} } } \right)^{T} \underline{\underline D} \left( { {m_{1} } - {m_{2} } } \right)}, $$
(12)

where m 1 and m 2 are two BPAs. \({\underline {\underline D} } \) is a 2N×2N matrix whose elements are \( \underline {\underline D} (A,B) = \frac {{|A \cap B|}}{{|A \cup B|}} \), where A,B∈P(Ω) are derived from m 1 and m 2, respectively.

2.4 Liu’s evidence conflict model

In traditional Dempster-Shafer evidence theory, the conflict coefficient K represents the degree of conflict between two bodies of evidence. Liu [35] noted that K cannot effectively measure the disagreement between two bodies of evidence. In the conflict model proposed by Liu [35], the pignistic betting distance and coefficient K are united to represent the degree of conflict.

Let m 1 and m 2 be two BPAs on the same frame of discernment, Ω. Then, the conflict model proposed by Liu is

$$ cf({m_{1}},{m_{2}}) = \left\langle {K,{d{\kern-.5pt}i{}f{\kern-2.5pt}BetP}} \right\rangle, $$
(13)

where K is the classical conflict coefficient of Dempster combination rule in (9), and d i f B e t P is the pignistic betting distance in (11). When K>ε and d i f B e t P>ε, m 1 and m 2 are regarded as being in conflict, where ε∈[0,1] is the threshold of the conflict tolerance. Because there does not exist an “absolutely meaningful threshold” of conflict tolerance that satisfies all pairs of BPAs [1], the value of ε is subjective and not fixed. Generally speaking, the closer ε is to 1, the greater the conflict tolerance.

3 The generalized theory

Dempster-Shafer theory has many merits in information fusion. It is similar to Bayesian theory, but has some large improvements. However, it still has some shortcomings. The computational complexity increases with the number of elements in the frame of discernment, which limits its real-world applications. Additionally, highly conflicting evidence causes counter-intuitive results. In the frame of discernment, the following two points may be the causes of the highly conflicting results. One is the incompleteness of the frame of discernment. For example, in military applications, suppose there are three targets (a, b, and c) on the frame of discernment. Then, the sensors can only recognize the different unions of these three targets. However, if there exists a new unknown target (d), the sensors cannot distinguish whether it is one of the previous three targets. In this situation, the recognition results will be multifarious, after combination, and there will be incorrect results. Another factor is the reliability of the sensors. Condition, disturbances, and other aspects of the sensor will influence the judgment results. There are some alternatives that overcome these shortcomings. Preprocessing the information or using approximation algorithms [26, 51] can reduce the computational complexity. Researchers have made significant efforts to solve the highly conflicting problem in recent years. Two typical solutions are the transferable belief model (TBM) [48] and Dezert-Smarandache theory (DSmT) [18]. One characteristic of the TBM model is related to the concepts of closed and open worlds. However, to the best of our knowledge, the TBM has only been applied to closed worlds. DSmT provides a new solution to the highly conflicting problem, but it is computationally complex. In summary, we still need a more reasonable model for solving for the highly conflicting problem. The new model should be able to handle incomplete frames of discernment, and should be no more computationally complex than traditional Dempster-Shafer theory. Taking this into consideration, we propose the new GET in this paper.

Note that traditional Dempster-Shafer theory is based on the frame of discernment, and has a constraint that the BPA m(∅) must be equal to 0. This is why classic Dempster-Shafer theory can only function in a closed world. In this paper, closed world means that the elements in the frame of discernment are exhaustive and complete. There are many cases of this in real-life. For example, a dice roll only has six possibilities (1, 2, 3, 4, 5 and 6). However, some applications lack complete knowledge, so we can only obtain a partial frame of discernment. As previously mentioned, the known enemy targets may be “a”, “b” and “c”, but there may exist a secret undeclared target, “d”. Then, the sensors cannot effectively recognize target “d”. In this situation, the frame of discernment {a, b, c} is incomplete. This is an open world situation. Along with enriched knowledge, an open world is absolute and a closed world is relative. Another example is SARS (severe acute respiratory syndrome). Before the appearance of SARS, the frame of discernment of pneumonia was not complete. Obviously, traditional Dempster-Shafer theory can only represent and process uncertain information in a closed world, which limits its applications. In this paper, we propose generalized evidence theory, which can be applied in an open world.

3.1 Basic concepts of generalized evidence theory

Definition 1

Suppose that U is a frame of discernment in an open world. Its power set, \({2_{G}^{U}}\), is composed of 2U propositions, ∀A⊂U. A mass function is a mapping \(m_{G}: {2_{G}^{U}} \to [0, 1]\) that satisfies

$$ \sum\limits_{A \in {2_{G}^{U}}} {{m_{G}}(A) = 1}. $$
(14)

Then, m G is the GBPA of the frame of discernment, U. The difference between GBPA and traditional BPA is the restriction of ∅, as shown in (5). Note that m G (∅)=0 is not necessary in GBPA. In other words, the empty set can also be a focal element. If m G (∅)=0, the GBPA reduces to a traditional BPA.

The ∅ is used to model an open world in GET. We should emphasize that the ∅ in GET is not a common empty set, it also can be a focal element or represents the union of focal elements that are out of the given frame of discernment. The \(m_{G}: {2_{G}^{U}} \to [0, 1]\) in Definition 1 indicates that the ∅ is the focal element outside of the frame of discernment, not the empty set in traditional BPA. Likewise, m G in (14) means that GBPA assigns some probability to the propositions beyond the frame of discernment. For simplicity, in the remainder of this paper, we have abbreviated GBPA to BPA, the mass function m G to m, and \({2_{G}^{U}}\) to 2U.

Similar to Dempster-Shafer theory, the generalized belief function (GBF) and generalized plausible function (GPL) in GET are defined as follows.

Definition 2

Given a GBPA m, the GBF is GBel: 2U→[0,1], and satisfies

$$\begin{array}{@{}rcl@{}} GBel(A) &=& \sum\limits_{B \subseteq A}{m(B)}, \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} GBel(\emptyset ) &=& m(\emptyset ). \end{array} $$
(16)

Definition 3

Given a GBPA m, the GPF is GPl: 2U→[0,1], and satisfies

$$\begin{array}{@{}rcl@{}} GPl(A) = \sum\limits_{B \cap A \ne \emptyset } {m(B)}, \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} GPl(\emptyset ) = m(\emptyset ). \end{array} $$
(18)

Note that in Definitions 2 and 3, G B e l(∅) and G P l(∅) are both equal to m(∅), which is logical. Because ∅ is a proposition beyond the frame of discernment, it cannot be supported by these propositions within the frame of discernment. Additionally, we do not know whether these propositions agree beyond the frame of discernment. GBF and GPF can be regarded as generalized lower and upper bounds of the support of subset A, respectively. It is obvious that

$$ GBel(A) \le GPl(A). $$
(19)

In the following, we give two examples of calculating the GBF and GPF, which show that the new GBF and GPF are generalizations of the traditional belief and plausibility functions, respectively.

Example 1

Suppose that there is a frame of discernment of {a,b,c}, and a GBPA is given as

$$m(a ) = 0.6; m(c) = 0.2; m(b,c) = 0.2.$$

The GBPA m assigns 0 to the empty set, i.e., m(∅)=0. In this case, the GBPA m degenerates into a traditional BPA. The GBF and GPF can be obtained using

$$\begin{array}{ll} GBel(a) &= 0.6; GBel(b) = 0; GBel(c)\\& = 0.2; GBel(b,c) = 0.4,\\ GPl(a) &= 0.6; GPl(b) = 0.2; GPl(c) \\&= 0.4; GPl(b,c) = 0.4. \end{array}$$

These results show that the values of the GBF and GPL in GBPA are the same as Bel and Pl in traditional BPA, where m(∅)=0.

Example 2

Suppose that there is a frame of discernment of {a,b,c}, and a GBPA is given as

$$m(a) = 0.6; m(b) = 0.1; m(b,c) = 0.2; m(\emptyset ) = 0.1.$$

In this case, the GBPA assign some value to the focal element ∅. The GBF and GPL are

$$\begin{array}{ll} GBel(a) &= 0.6; GBel(b) = 0.1; GBel(c) \\&= 0; GBel(b,c) = 0.3; GBel(\emptyset ) = 0.1,\\ GPl(a) &= 0.6; GPl(b) = 0.3; GPl(c)\\& = 0.2; GPl(b,c) = 0.3; GPl(\emptyset ) = 0.1. \end{array}$$

3.2 Generalized combination rule (GCR)

The classic Dempster combination rule can be used to combine two BPAs (m 1 and m 2) to yield a new BPA (m). Based on the classic Dempster combination rule, the generalized combination rule (GCR) is defined as follows.

Definition 4

In generalized evidence theory, ∅ 1∩∅ 2=∅ means that the intersection between two empty sets is still an empty set. Given two GBPAs (m 1 and m 2), the generalized combination rule (GCR) is defined as follows.

$$\begin{array}{@{}rcl@{}} m(A) &=& \frac{{(1 - m(\emptyset ))\sum\limits_{B \cap C = A} {{m_{1}}(B) \cdot {m_{2}}(C)} }}{{1 - K}}, \end{array} $$
(20)
$$\begin{array}{@{}rcl@{}} K &=& \sum\limits_{B \cap C = \emptyset } {{m_{1}}(B) \cdot {m_{2}}(C)}, \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} m(\emptyset ) &=& {m_{1}}(\emptyset ) \cdot {m_{2}}(\emptyset ), \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} m(\emptyset ) &=& 1 \quad if \;\; and \;\; only \;\; if \quad K =1. \end{array} $$
(23)

The characteristics of the GCR in (20–23) can be summarized as follows.

  1. (1)

    When m(∅)=0, the GCR degenerates to the classic Dempster combination rule.

  2. (2)

    Two empty sets can be combined by multiplying their GBPA values.

  3. (3)

    The factor 1/(1−K) in (20) is a normalized process that reassigns the GBPA values after deducting the m(∅) obtained from (22). In other words, we multiply the GBPAs with non-empty intersections to accumulate them, and then amplify the results 1/(1−K) times.

  4. (4)

    Because ∅ 1∩∅ 2=∅, the GBPA value of conflict coefficient K is obtained after superposing (9) and (22).

Three properties of generalized evidence theory (GET) are as follows.

Property 1

When m(∅)=0, GBPA degenerates to traditional BPA. More generally, if GBPA just assigns single elements, GBPA degenerates to probability theory.

Property 2

For the GCR of GET, if m(∅)=0, then GCR degenerates to the classic Dempster combination rule. More generally, when GBPAs just assign single elements, the results of GCR are the same as those of Bayesian probability.

Property 3

Similar to Dempster combination rule, GCR is commutative and associative. This means that the combination results using the GCR are unrelated to the order of the combination.

3.3 Generalized evidence distance

The generalized evidence distance (GED) in GET is defined as follows.

Definition 5

Let m 1 and m 2 be two GBPAs on the frame of discernment U. The generalized evidence distance between m 1 and m 2 is defined as

$$ {d_{GBPA}}({m_{1}},{m_{2}}) = \sqrt {\frac{1}{2}{{\left( {\overrightarrow {{m_{1}}} - \overrightarrow {{m_{2}}} } \right)}^{T}}\overline D \left( {\overrightarrow {{m_{1}}} - \overrightarrow {{m_{2}}} } \right)}, $$
(24)

where \({\overline D }\) is a 2N×2N matrix with elements

$$ {\overline D}(A,B) = \frac{{\left| {A \cap B} \right|}}{{\left| {A \cup B} \right|}};A,B \in P\left( U \right). $$
(25)

It is calculated using

$${d_{GBPA}}({m_{1}},{m_{2}}) = \sqrt {\frac{1}{2}\left( {{{\left\| {\overrightarrow {{m_{1}}} } \right\|}^{2}} + {{\left\| {\overrightarrow {{m_{2}}} } \right\|}^{2}} - 2\left\langle {\overrightarrow {{m_{1}}} ,\overrightarrow {{m_{2}}} } \right\rangle } \right)} $$

, where \({\left \| {\overrightarrow m } \right \|^{2}} = \left \langle {\overrightarrow m ,\overrightarrow m } \right \rangle \), \(\left \langle {\overrightarrow m ,\overrightarrow m } \right \rangle \) is the inner product of the two vectors, i.e.,

$$\begin{array}{l}\left\langle {\overrightarrow {{m_{1}}} ,\overrightarrow {{m_{2}}} } \right\rangle = \sum\limits_{i = 1}^{{2^{N}}} {\sum\limits_{j = 1}^{{2^{N}}} {{m_{1}}({A_{i}}){m_{2}}({A_{j}})} } \frac{{\left| {{A_{i}} \cap {B_{i}}} \right|}}{{\left| {{A_{i}} \cup {B_{i}}} \right|}};\\{A_{i}},{B_{j}} \in P(U ).\end{array}$$

3.4 Numerical examples of GCR

In this subsection, we use numerical examples to demonstrate the GCR combination process.

Example 3

Assume a frame of discernment U={a,b,c}, and that two GBPAs are given as

$$\begin{array}{l} {m_{1}}(a) = 0.5; {m_{1}}(a,b) = 0.5\\ {m_{2}}(a) = 0.5; {m_{2}}(b) = 0.3; {m_{2}}(U ) = 0.2. \end{array}$$

We combine m 1 and m 2 such that

$$m(\emptyset ) = {m_{1}}(\emptyset ) \cdot {m_{2}}(\emptyset ) = 0 \times 0 = 0$$

and

$$K = {m_{1}}(a)\cdot{m_{2}}(b) = 0.5 \times 0.3 = 0.15.$$

Then,

$$\begin{array}{@{}rcl@{}} m(a) &=& \frac{{1 - m(\emptyset )}}{{1 - K}} \times (m_{1}(a)\times (m_{2}(a) + m_{2}(U ))\\ && + m_{2}(a) \times m_{1}(a,b)). \\ &=&\frac{{(1 - 0) \times (0.5 \times (0.5 + 0.2) + 0.5 \times 0.5)}}{{1 - 0.15}} \\&=& 0.706.\\ m(b) &=& \frac{{1 - m(\emptyset )}}{{1 - K}} \times {m_{1}}(a,b) \times {m_{2}}(b)\\ &=& \frac{{(1 - 0) \times 0.5 \times 0.3}}{{1 - 0.15}} = 0.176.\\ m(a,b)&=&\frac{{1 - m(\emptyset )}}{{1 - K}} \times {m_{1}}(a,b)\times {m_{2}}(U )\\ &=& \frac{{(1 - 0) \times 0.5 \times 0.2}}{{1 - 0.15}} = 0.118.\\ &&m(U ) = 0. \end{array} $$

This example shows that the GCR is the same as the classic Dempster combination rule when m(∅)=0.

Example 4

Suppose that the frame of discernment is U={a,b,c} and two GBPAs are given as

$$\begin{array}{l} m_{1}(a) = 0.2; m_{1}(b) = 0.2; m_{1}(\emptyset ) = 0.6,\\ m_{2}(a) = 0.2; m_{2}(b,c) = 0.1; m_{2}(\emptyset ) = 0.7 \end{array}. $$

In this example, we used an intersection table to calculate K in the GCR. Using Table 1, we can easily obtain K (the conflicting coefficient in GET). That is,

$$\begin{array}{lll} K &=& m_{1} (a) \cdot m_{2} (b,c) + m_{1} (a) \cdot m_{2} (\emptyset ) + m_{1} (b) \cdot m_{2} (a) \\ &&+ m_{1} (b) \cdot m_{2} (\emptyset) + m_{1} (\emptyset ) \cdot m_{2} (a) + m_{1} (\emptyset ) \cdot m_{2} (b,c)\\ &&+ m_{1} (\emptyset ) \cdot m_{2} (\emptyset ), \\ &=& 0.2 \times 0.1 + 0.2 \times 0.7 + 0.2 \times 0.2 + 0.2 \times 0.7 \\ &&+ 0.6 \times 0.2+ 0.6 \times 0.1 + 0.6 \times 0.7, \\ &=& 0.02 + 0.14 + 0.04 + 0.14 + 0.12 + 0.06 + 0.42, \\ &=& 0.94. \\ \end{array} $$

Then,

$$m(\emptyset ) = {m_{1}}(\emptyset ) \times {m_{2}}(\emptyset ) = 0.6 \times 0.7 = 0.42,$$

so

$$\begin{array}{l} m(a)\! =\! \frac{{1 - m(\emptyset )}}{{1 - K}} \times {m_{1}}(a){m_{2}}(a) = \frac{{(1 - 0.42) \times 0.2 \times 0.2}}{{1 - 0.94}} = 0.387,\\ m(b)\! =\! \frac{{1 - m(\emptyset )}}{{1 - K}} \!\times\! {m_{1}}(b){m_{2}}(b,c)\! =\! \frac{{(1 - 0.42) \times 0.2 \times 0.1}}{{1 - 0.94}} \,=\, 0.193,\\ m(c) = 0. \end{array}$$

The final results are

$$\begin{array}{l} m(a) = 0.347; m(b) = 0.193; m(c) = 0; m(\emptyset ) = 0.42. \end{array}$$
Table 1 Intersection table for combining m 1 and m 2 in Example 4 using GCR
Full size table

It is obvious that the traditional Dempster combination rule is not suitable in this situation, because m(∅)≠0. Clearly, after we determine the value of m(∅), GCR redistributes the remaining probability to the other nonempty sets. In this example, the probability of m(c) is 0, because the single set {c} is not supported by either of the two BPAs in the frame of discernment. That is to say, we increase the probability of the single sets {a} and {b} because they are both more or less supported by the two GBPAs.

Example 5

Suppose that the frame of discernment is U={a,b,c}, and two GBPAs are given as

$$\begin{array}{l} {m_{1}}(a) = 0.2;{m_{1}}(\emptyset ) = 0.8,\\ {m_{2}}(b) = 0.5;{m_{2}}(\emptyset ) = 0.5. \end{array}$$

The conflicting coefficient K in GET is

$$\begin{array}{ll} K &= {m_{1}}(a)({m_{2}}(b) + {m_{2}}(\emptyset )) + {m_{1}}(\emptyset )({m_{2}}(b) + {m_{2}}(\emptyset )),\\ &= 0.2 \times (0.5 + 0.5) + 0.8 \times (0.5 + 0.5)\\ &= 1. \end{array}$$

Thus,

$$m(\emptyset ) =1.$$

From the GCR view, we can first obtain that m(∅)=m 1(∅)×m 2(∅) = 0.4. However, because the other two propositions are not supported by each other, the remaining probability cannot be assigned to either of them, and is reassigned to m(∅). Therefore, m(∅) is assigned twice the amount, and m(∅) = 0.4 + 0.6 = 1. We believe that this is reasonable. When the two GBPAs are highly conflicting and do not support each other, we should consider that the frame of discernment is incomplete.

Example 6

(Comparison with the belief revision method [5]) As discussed in [5], the belief revision method is also associated with knowledge representation and incorporating new information. In this example, we compared the proposed GCR with the belief revision method [5].

As in [5], we initially assume that

$$\begin{array}{@{}rcl@{}} P(\{a, b, c\})\!&=&\!0.15; P(\{a, b, \bar{c}\})\,=\,0.15; \!P(\{a, \bar{b}, c\})\,=\,0.1;\\ P(\{a, \bar{b}, \bar{c}\})&=&0.1;\\ P(\{\bar{a}, b, c\})\!&=\!&0.15; \!P(\{\bar{a}, b, \bar{c}\})\,=\,0.15; \!P(\{\bar{a}, \bar{b}, c\})\,=\,0.1;\\ P(\{\bar{a}, \bar{b}, \bar{c}\})&=&0.1.\end{array} $$

If we obtain an observation of a with reliability 0.8, the belief revision method derives a revised belief of

$$P(a,0.8)(\{a, b, c\})=0.24; P(a,0.8)(\{a, b, \bar{c}\})=0.24; $$
$$P(a,0.8)(\{a, \bar{b}, c\})=0.16; P(a,0.8)(\{a, \bar{b}, \bar{c}\})=0.16;$$
$$P(a,0.8)(\{\bar{a}, b, c\})=0.06; P(a,0.8)(\{\bar{a}, b, \bar{c}\})=0.06; $$
$$P(a,0.8)(\{\bar{a}, \bar{b}, c\})=0.04; P(a,0.8)(\{\bar{a}, \bar{b}, \bar{c}\})=0.04.$$

Now, let us consider this case in the GBT framework. The initial belief can be considered a GBPA, that is,

$$\begin{array}{@{}rcl@{}} m_{1}(\{a, b, c\})&=&0.15; m_{1}(\{a, b, \bar{c}\})=0.15; m_{1}(\{a, \bar{b}, c\})\\ &=&0.1; m_{1}(\{a, \bar{b}, \bar{c}\})=0.1;\\ m_{1}(\{\bar{a}, b, c\})&=&0.15; m_{1}(\{\bar{a}, b, \bar{c}\})=0.15; m_{1}(\{\bar{a}, \bar{b}, c\})\\&=&0.1; m_{1}(\{\bar{a}, \bar{b}, \bar{c}\})=0.1. \end{array} $$

Because this example is in a closed world, m 1(∅)=0. In GET, an observation of a with reliability 0.8 means that a occurs with a probability 0.8 despite b and c, and a does not occur with a probability 0.2 regardless of b and c. So in GET, the observation can be expressed by

$$m_{2}(\{a, b, c\}, \{a, b, \bar{c}\}, \{a, \bar{b}, c\}, \{a, \bar{b}, \bar{c}\})=0.8;$$
$$m_{2}(\{\bar{a}, b, c\}, \{\bar{a}, b, \bar{c}\}, \{\bar{a}, \bar{b}, c\}, \{\bar{a}, \bar{b}, \bar{c}\})=0.2.$$

Based on the GCR, we can combine m 1 (the initial knowledge) and m 2 (new observation). The calculation process is as follows. The intersection table for combining m 1 and m 2 is shown in Table 2. Using this,

$$\begin{array}{@{}rcl@{}} K&=&\sum \emptyset= 0.12+0.12+0.08+0.08+0.03+0.03\\ &&+0.02+0.02=0.5, \end{array} $$

and m(∅)=m 1(∅)m 2(∅)=0×0=0.

Table 2 Intersection table for combining m 1 and m 2 in Example 6
Full size table

Now,

$$\begin{array}{@{}rcl@{}} m(\{a, b, c\}) &=&\!\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{a, b, c\})\\&& \!\times m_{2}(\{a, b, c\}, \{a, b, \bar{c}\}, \{a, \bar{b}, c\}, \{a, \bar{b}, \bar{c}\}))\\ &=\!&\frac{(1-0) \times 0.15 \times 0.8}{1-0.5}=0.24,\\ m(\{a, b, \bar{c}\}) &=&\!\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{a, b, \bar{c}\}) \\&&\!\times m_{2}(\{a, b, c\}, \{a, b, \bar{c}\}, \{a, \bar{b}, c\}, \{a, \bar{b}, \bar{c}\}))\\ &=&\!\frac{(1-0) \times 0.15 \times 0.8}{1-0.5}=0.24, \end{array} $$
$$\begin{array}{@{}rcl@{}} m(\{a, \bar{b}, c\}) &=&\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{a, \bar{b}, c\}) \\&&\times m_{2}(\{a, b, c\}, \{a, b, \bar{c}\}, \{a, \bar{b}, c\}, \{a, \bar{b}, \bar{c}\}))\\ &=&\frac{(1-0) \times 0.1 \times 0.8}{1-0.5}=0.16,\\ m(\{a, \bar{b}, \bar{c}\}) &=&\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{a, \bar{b}, \bar{c}\}) \\&&\times m_{2}(\{a, b, c\}, \{a, b, \bar{c}\}, \{a, \bar{b}, c\}, \{a, \bar{b}, \bar{c}\}))\\ &=&\frac{(1-0) \times 0.1 \times 0.8}{1-0.5}=0.16,\\ m(\{\bar{a}, b, c\}) &=&\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{\bar{a}, b, c\}) \\&&\times m_{2}(\{\bar{a}, b, c\}, \{\bar{a}, b, \bar{c}\}, \{\bar{a}, \bar{b}, c\}, \{\bar{a}, \bar{b}, \bar{c}\}))\\ &=&\frac{(1-0) \times 0.15 \times 0.2}{1-0.5}=0.06,\\ m(\{\bar{a}, b, \bar{c}\}) &=&\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{\bar{a}, b, \bar{c}\}) \\&&\times m_{2}(\{\bar{a}, b, c\}, \{\bar{a}, b, \bar{c}\}, \{\bar{a}, \bar{b}, c\}, \{\bar{a}, \bar{b}, \bar{c}\}))\\ &=&\frac{(1-0) \times 0.15 \times 0.2}{1-0.5}=0.06,\\ m(\{\bar{a}, \bar{b}, c\}) &=&\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{\bar{a}, \bar{b}, c\}) \\&&\times m_{2}(\{\bar{a}, b, c\}, \{\bar{a}, b, \bar{c}\}, \{\bar{a}, \bar{b}, c\}, \{\bar{a}, \bar{b}, \bar{c}\}))\\ &=&\frac{(1-0) \times 0.1 \times 0.2}{1-0.5}=0.04,\\ m(\{\bar{a}, \bar{b}, \bar{c}\}) &=&\frac{1-m(\emptyset)}{1-K} \times (m_{1}(\{\bar{a}, \bar{b}, \bar{c}\}) \\&&\times m_{2}(\{\bar{a}, b, c\}, \{\bar{a}, b, \bar{c}\}, \{\bar{a}, \bar{b}, c\}, \{\bar{a}, \bar{b}, \bar{c}\}))\\ &=&\frac{(1-0) \times 0.1 \times 0.2}{1-0.5}=0.04. \end{array} $$

Moreover, if we iterate the process and again observe a with the same reliability, the revised belief P(a,0.8)(a,0.8) can also be obtained using the belief revision method. Correspondingly, the results derived from the GCR are denoted GCR(m 1,m 2,m 3), where m 3 represents the same observation of a with reliability 0.8.

The above results are displayed in Table 3. The GCR(m 1,m 2) results are the same as the revised belief P(a,0.8), GCR(m 1,m 2,m 3), and P(a,0.8)(a,0.8). Therefore, the GCR is consistent with the belief revision method. Meanwhile, note that the belief revision method is only suitable in a closed world, and that the GCR is inherently more useful because it can be applied in an open world.

Table 3 Comparison of the GCR and belief revision methods
Full size table

4 Application and discussion

4.1 The m(∅) in Dempster-Shafer evidence and GET

In classic Dempster-Shafer theory, m(∅)=0 is indispensable. From this point of view, ∅ is a proposition without any support from other propositions. There is no physical meaning to ∅ in Dempster-Shafer theory. ∅ was first noted and assigned to m(∅) in the TBM proposed by Smets [48]. In TBM, if there is a lot of conflict between two bodies of evidence, the conflict is assigned to m(∅). The basic belief assignment (BBA) in TBM is used to distinguish the method from traditional BPA in Dempster-Shafer theory. However, BBA and BPA are both essentially assigned to these nonempty sets. In other words, the restriction condition of m(∅)=0 is still necessary. The logic behind this approach is questionable. If the problem is in an open world, we should assign the value to m(∅) when we generate the BBAs in TBM. Additionally, it is a weak approach to dealing with conflict. Yager [54] proposed a method where the conflicting values are assigned to the whole set Ω when the evidence is highly contradictory. Yager’s method is contentious. In GET, while the GBPAs are generated, m(∅)≠0 is permissible, which is easy to understand. That is, there may exist some hypotheses or propositions beyond the fixed frame of discernment. The value of m(∅) indicates the open world degree of the frame of discernment. The GET proposed in this paper is an extension of classic Dempster-Shafer theory, and can express and deal with more uncertain information in the open world than Dempster-Shafer theory in the closed world.

4.2 Modified Liu’s conflict model

As mentioned in Section 2.4, Liu analyzed the drawbacks of the classic conflict coefficient, K, and proposed a conflict model. The main idea is to construct two tuples using the pignistic betting distance d i f B e t P from TBM [49] and the classic conflict coefficient K from Dempster-Shafer theory [6, 46]. The union of these is used to represent degree of conflict. If only d i f B e t P is large, then the two pieces of evidence cannot be regarded as conflicting. If only K is large, then the two pieces of evidence can also not be viewed as conflicting. The conflict is only ascertained by the union of d i f B e t P with K. This conflict model is very interesting, because it provides a new way of thinking regarding methods for expressing the conflict between two bodies of evidence. The following is a numerical example of Liu’s conflict model.

Example 7

Let a frame of discernment be Ω={a,b,c}, and consider two BPAs m 1 and m 2 defined as

$$\begin{array}{l} {m_{1}}(a) = \frac{1}{3};{m_{1}}(b) = \frac{1}{3};{m_{1}}(c) = \frac{1}{3},\\ {m_{2}}(a,b,c) = 1. \end{array}$$

Because K=0 and d i f B e t P=0, c f 12(K,d i f B e t P)=〈0,0〉, so the two BPAs are regarded as not being in conflict. However, this is obviously irrational, because the two BPAs provide different information. m 1 is definite, and m 2 is total ignorance. So Liu’s conflict model is still not suitable for reasonably expressing the conflict between evidence.

This example demonstrates that “the same probability of occurrence” is the same as “total ignorance of the system” in Liu’s conflict model. However, the real situation is not so simple. If we know nothing about the system (i.e., m(Ω)=1), then m(a)=m(b)=0.5; m(a)=0.7,m(b)=0.3; m(a)=1,m(b)=0 and so forth are possible, and the probability of uncertainty for the system is maximized. Thus, the pignistic betting distance cannot distinguish between situations with the same probabilities or total ignorance, and is not an appropriate conflict model. We propose a modified evidence conflict model that is based on Jousselme’s evidence distance [28].

Definition 6

Suppose that there are two different BPAs on the same frame of discernment Ω, and that the modified evidence conflict model is defined as

$$ cf({m_{1}},{m_{2}}) = \left\langle {K,dis} \right\rangle, $$
(26)

where K is the classic conflict coefficient in Dempster-Shafer theory (see (9)), and dis is the evidence distance in (12).

4.3 Conflict model of GET

In the previous subsection, we modified Liu’s conflict model using (26) to make it more reasonable. However, this conflict model is still in a closed world, and cannot be applied to an open world where the frame of discernment may be incomplete. With this in mind, we propose a new conflict model for GET.

Definition 7

Assume that there are two GBPAs, m 1 and m 2, on the frame of discernment U, and that the generalized conflict model is

$$ c{f_{G}}({m_{1}},{m_{2}}) = \left\langle {K,dis} \right\rangle, $$
(27)

where K is the generalized conflict coefficient in (21), and dis is the generalized evidence distance in (24).

Compared with existing methods, this new proposed generalized conflict model can handle information on the incomplete frame of discernment. When the frame of discernment is complete, the generalized conflict coefficient and generalized evidence distance reduce to the classical coefficient and classical evidence distance. Additionally, (27) degenerates to (26).

The following examples demonstrate how to apply the generalized conflict coefficient and generalized conflict model.

Example 8

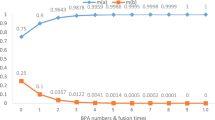
Consider two GBPAs, m 1 and m 2, on the frame of discernment. The first group of GBPAs varies. They start at m 1(a)=1 and m 1(∅)=0, and then m 1(a) progressively decreases by 0.1 and m(∅) progressively increases by 0.1 at each time step. The second group of GBPAs also varies. They start at m 2(a)=1 and m 2(∅)=0, and then m 2(a) progressively decreases by 0.1 and m 1(∅) progressively increases by 0.1 at each time step. Then, the generalized conflict coefficient between the two GBPAs is shown in Fig. 1.

Fig. 1
figure 1

Generalized conflict coefficient between two GBPAs

Full size image

Figure 1 indicates that, when m 1(a)=1, m 1(∅)=0, m 2(a)=1, and m 2(∅)=0, the generalized conflict coefficient is minimized, the proposition {a} is absolutely supported by the system, and the frame of discernment is complete. While m 2(a) progressively decreases by 0.1 at each time step, m 1(∅) progressively increases by 0.1 and the generalized conflict coefficient also gradually increases. This situation indicates that the frame of discernment is becoming more incomplete. According to GCR, when m(∅)=1 appears in any of these GBPAs, the generalized conflict coefficient achieves its maximum of 1.

Example 9

Suppose that there are two GBPAs on the frame of discernment. The first group of GBPAs varies. It starts with m 1(a)=0 and m 1(∅)=1. m 1(a) progressively increases by 0.1 and m(∅) progressively decreases by 0.1 at each time step. The second group of GBPAs also varies. It starts with m 2(a)=0 and m 2(∅)=1. m 2(a) progressively increases by 0.1 and m 2(∅) progressively decreases by 0.1 at each time step. Then, the generalized evidence distance between the two GBPAs is as shown in Fig. 2. Figure 2 shows that the generalized evidence distance on the diagonal is 0, because the two GBPs are the same.

Fig. 2
figure 2

Generalized evidence distance between two GBPAs

Full size image

Example 10

Consider two GBPAs on the same frame of discernment, and two given GBPAs,

$$\begin{array}{l} {m_{x1}}(b) = 0.1;{m_{x1}}(\emptyset ) = 0.9,\\ {m_{x2}}(b) = 0.1;{m_{x2}}(\emptyset ) = 0.9. \end{array}$$

The GET conflict model is

$$c{f_{G}}({m_{1}},{m_{2}}) = \left\langle {0.81,0} \right\rangle, $$

and is illustrated in Fig. 3.

Fig. 3
figure 3

Two samples with different classes

Full size image

Figure 3 indicates that there is just one class b on the frame of discernment. The two dotted triangles represent the classes a and c, both of which do not appear on this frame of discernment. In fact, sensors x1 and x2 belong to classes a and c, respectively. If we only consider the generalized evidence distance, we will obtain an incorrect result. This example points out that generalized conflict coefficient is a better measure than the generalized evidence distance on an incomplete frame of discernment.

The following two examples are applied to the complete frame of discernment with m(∅)=0.

Example 11

Consider a frame of discernment Ω={a,b}. The first fixed BPA is such that m 1(a,b)=1. The second varying BPA begins with m 2(a)=0;m 2(b)=1. m 2(a) progressively increases by 0.1 and m 2(b) decreases by 0.1 at each time step. Then, the evidence distance and pignistic betting distance between m 1 and m 2 are as shown in Fig. 4. Figure 4 shows that when m 2(a)=0.5 and m 2(b)=0.5, the pignistic betting distance between two BPAs is 0, which indicates that there is no conflict between BPAs. However, at this time step, the evidence distance is 0.5, which indicates that there is conflict between the BPAs. It is obvious that we should use evidence distance and not pignistic betting distance as a measure of the conflict for a complete frame of discernment.

Fig. 4
figure 4

Comparisons of evidence distance and pignistic betting distance

Full size image

Example 12

Suppose that we have a frame of discernment of Ω={1,2,3⋯20}, and two BPAs are defined as

$$\begin{array}{l} {m_{1}}(7 ) = 0.6;{m_{1}}(A) = 0.4,\\ m_{2}(1,2,3 ) = 1, \end{array}$$

where A is a varying subset of Ω. A increments one more element each time, starting at A= {1}, and ending with Case 20, when A={1,2,3⋯20}. The evidence distance and classic conflict coefficient K between two BPAs are shown in Table 4 and Fig. 5.

Fig. 5
figure 5

Comparison of the new proposed conflict coefficient with the classic conflict coefficient

Full size image
Table 4 Comparison of the new proposed conflict coefficient with the classic conflict coefficient
Full size table

Table 4 and Fig. 5 show that, regardless of the subset A, the classic conflict coefficient K is always 0.6. This is irrational. The generalized evidence distance depends on A, and can effectively measure the conflict. That means the generalized evidence distance for measuring the conflict is better than the generalized conflict coefficient, in the case of a complete frame of discernment.

These numerical examples show how to apply this new conflict model. When the frame of discernment is incomplete and m(∅)≠0, the two-tuples of the conflict model should mainly depend on the generalized conflict coefficient. However, when the frame of discernment is complete and m(∅)=0, the two-tuples of the conflict model should mainly depend on the generalized evidence distance.

5 Conclusions

In this paper, we proposed a novel theory called GET. Some key points are given in the following.

First, evidence theory is an efficient tool for fusing information in an uncertain environment. If we definitely know that we are in a closed world, Dempster combination rule is enough to combine evidence from different sources. If the evidence is conflicting, the conflicting evidence can be combined by considering its reliability.

Second, GET is an extension of Dempster-Shafer theory, in which the strict restriction condition of m(∅)=0 is abandoned. In GET, ∅ is regarded as an element with the same properties as the other elements. It represents unknown, but not a common empty.

This is why GET can better fuse uncertain information in an open world, when compared with Dempster-Shafer theory. GET inherits all the benefits of Dempster-Shafer theory, but expands its scope to an open world. When the frame of discernment is complete and m(∅)=0, GET degenerates to Dempster-Shafer theory. Additionally, the GCR in GET is distinct from the Dempster combination rule.

Third, we proposed the generalized conflict model based on GET. We have demonstrated how to apply the generalized conflict model under different conditions. When the frame of discernment is incomplete, the measure of the generalized conflict should mainly be based on the generalized conflict coefficient. When the frame of discernment is complete, the measure of the generalized conflict should mainly be based on the evidence distance.

An increasing amount of research is focusing on modeling epistemic uncertainty [43]. We believe that the proposed evidence theory with the non-zero empty set will provide a promising way to model epistemic uncertainty in the future. Additionally, note that, besides conflict management in an open world, we should also pay attention to the exclusive condition in Dempster-Shafer evidence theory. An ongoing area of investigation involves D numbers theory, which focuses on mutual exclusion in evidence theory. In classical evidence theory, we assume that each hypothesis is exclusive. However, this is not reasonable in the real world. Various linguistic variables and fuzzy numbers cannot be exclusive for each element. For example, given two linguistic values “Good (G)” and “Very Good (VG)”, m(G,V G)=0.8 is not accepted under Dempster-Shafer evidence theory because the two linguistic values are not exclusive. To address this limitation, a novel theory called D numbers theory [12] was proposed. D numbers and the GET proposed in this paper are generalizations of evidence theory, providing a more flexible and reasonable way to handle uncertainty in the real world [9–11, 34].