Skip to main content
SpringerLink
Log in

Non-uniform rational B-spline based free vibration analysis of axially functionally graded tapered Timoshenko curved beams

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

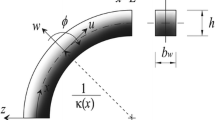
The free vibration of axially functionally graded (FG) tapered Timoshenko curved beams is studied with the numerical approach. By using the non-uniform rational B-spline (NURBS) basis functions, the exact geometry and the generalized displacement field are formulated. Variable geometric parameters and material properties, including the curvature, cross-sectional area, area moment of inertia, mass density, and Young’s modulus, are expanded as functions of the coordinate in a parametric domain. Based on Hamilton’s principle, the weak formulation is derived by applying a refined constitutive relation which considers the thickness effect. Natural frequencies and mode shapes are obtained from the eigenvalue equation. Circular, elliptic, and parabolic curved beams are considered in numerical examples. The obtained results are in good agreement with those in the existing studies and those calculated by the finite element software ANSYS. Moreover, the effects of the material gradient, taper ratio, slenderness ratio, and height-span ratio on vibration behaviors are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. KOIZUMI, M. Functionally gradient materials the concept of FGM. Ceramic Transactions, 34, 3–10 (1993)

    Google Scholar 

  2. OBATA, Y. and NODA, N. Transient thermal stresses in a plate of functionally gradient material. Ceramic Transactions, 34, 403–410 (1993)

    Google Scholar 

  3. THANG, P. T. and LEE, J. Free vibration characteristics of sigmoid-functionally graded plates reinforced by longitudinal and transversal stiffeners. Ocean Engineering, 148, 53–61 (2018)

    Article  Google Scholar 

  4. ELISHAKOFF, I. and CANDAN, S. Apparently first closed-form solutions for vibrating inhomogeneous beams. International Journal of Solids and Structures, 38, 3411–3441 (2001)

    Article  MathSciNet  Google Scholar 

  5. ELISHAKOFF, I. and GUEDE, Z. Analytical polynomial solutions for vibrating axially graded beams. Mechanics of Advanced Materials and Structures, 11, 517–533 (2004)

    Article  Google Scholar 

  6. CALIO, I. and ELISHAKOFF, I. Closed-form trigonometric solutions for inhomogeneous beam-columns on elastic foundation. International Journal of Structural Stability and Dynamics, 4, 139–146 (2004)

    Article  Google Scholar 

  7. CALIO, I. and ELISHAKOFF, I. Closed-form solutions for axially graded beam-columns. Journal of Sound and Vibration, 280, 1083–1094 (2005)

    Article  Google Scholar 

  8. WU, L., WANG, Q., and ELISHAKOFF, I. Semi-inverse method for axially FG beams with an anti-symmetric vibration mode. Journal of Sound and Vibration, 284, 1190–1202 (2005)

    Article  Google Scholar 

  9. LI, X. F., KANG, Y. A., and WU, J. X. Exact frequency equations of free vibration of exponentially functionally graded beams. Applied Acoustics, 74(3), 413–420 (2013)

    Article  Google Scholar 

  10. SARKAR, K. and GANGULI, R. Closed-form solutions for axially FG Timoshenko beams having uniform cross-section and fixed-fixed boundary condition. Composites Part B-Engineering, 58, 361–370 (2014)

    Article  Google Scholar 

  11. ALSHORBAGY, A. E., ELTAHER, M. A., and MAHMOUD, F. F. Free vibration characteristics of a functionally graded beam by finite element method. Applied Mathematical Modelling, 35, 412–425 (2011)

    Article  MathSciNet  Google Scholar 

  12. ŠALINIĆ, S., OBRADOVIĆ, A., and TOMOVIĆ, A. Free vibration analysis of axially FG tapered, stepped, and continuously segmented rods and beams. Composites Part B-Engineering, 150, 135–143 (2018)

    Article  Google Scholar 

  13. LIU, P., LIN, K., LIU, H., and QIN, R. Free transverse vibration analysis of axially FG tapered Euler-Bernoulli beams through spline finite point method. Shock and Vibration, 5891030 (2016)

    Google Scholar 

  14. HUANG, Y. and LI, X. F. A new approach for free vibration of axially FG beams with non-uniform cross-section. Journal of Sound and Vibration, 329, 2291–2303 (2010)

    Article  Google Scholar 

  15. HUANG, Y., YANG, L. E., and LUO, Q. Z. Free vibration of axially FG Timoshenko beams with non-uniform cross-section. Composites Part B-Engineering, 45, 1493–1498 (2013)

    Article  Google Scholar 

  16. ZHAO, Y., HUANG, Y., and GUO, M. A novel approach for free vibration of axially FG beams with non-uniform cross-section based on Chebyshev polynomials theory. Composite Structures, 168, 277–284 (2017)

    Article  Google Scholar 

  17. ATTARNEJAD, R., SEMNANI, S. J., and SHAHBA, A. Basic displacement functions for free vibration analysis of non-prismatic timoshenko beams. Finite Elements in Analysis and Design, 46(10), 916–929 (2010)

    Article  MathSciNet  Google Scholar 

  18. SHAHBA, A., ATTARNEJAD, R., and HAJILAR, S. A mechanical-based solution for axially FG tapered Euler-Bernoulli beams. Mechanics of Advanced Materials and Structures, 20, 696–707 (2013)

    Article  Google Scholar 

  19. TANG, A. Y., WU, J. X., LI, X. F., and LEE, K. Exact frequency equations of free vibration of exponentially non-uniform functionally graded Timoshenko beams. International Journal of Mechanical Sciences, 89, 1–11 (2014)

    Article  Google Scholar 

  20. RAJASEKARAN, S. and TOCHAEI, E. N. Free vibration analysis of axially functionally graded tapered Timoshenko beams using differential transformation element method and differential quadrature element method of lowest-order. Meccanica, 49, 995–1009 (2014)

    Article  MathSciNet  Google Scholar 

  21. SHAHBA, A., ATTARNEJAD, R., MARVI, M. T., and HAJILAR, S. Free vibration and stability analysis of axially FG tapered Timoshenko beams with classical and non-classical boundary conditions. Composites Part B-Engineering, 42, 801–808 (2011)

    Article  Google Scholar 

  22. QATU, M. S. Theories and analyses of thin and moderately thick laminated composite curved beams. International Journal of Solids and Structures, 30, 2743–2756 (1993)

    Article  Google Scholar 

  23. OH, S. J., LEE, B. K., and LEE, I. W. Natural frequencies of non-circular arches with rotatory inertia and shear deformation. Journal of Sound and Vibration, 219, 23–33 (1999)

    Article  Google Scholar 

  24. TSENG, Y. P., HUANG, C. S., and LIN, C. J. Dynamic stiffness analysis for in-plane vibrations of arches with variable curvature. Journal of Sound and Vibration, 207, 15–31 (1997)

    Article  Google Scholar 

  25. HUANG, C. S., TSENG, Y. P., LEISSA, A. W., and NIEH, K. Y. An exact solution for inplane vibrations of an arch having variable curvature and cross section. International Journal of Mechanical Sciences, 40, 1159–1173 (1998)

    Article  Google Scholar 

  26. TSENG, Y. P., HUANG, C. S., and KAO, M. S. In-plane vibration of laminated curved beams with variable curvature by dynamic stiffness analysis. Composite Structures, 50, 103–114 (2000)

    Article  Google Scholar 

  27. ROSSI, R. E., LAURA, P. A., and VERNIERE, P. L. In-plane vibrations of cantilvered non-circular arcs of non-uniform cross-section with a tip mass. Journal of Sound and Vibration, 129, 201–213 (1989)

    Article  Google Scholar 

  28. OH, S. J., LEE, B. K., and LEE, I. W. Free vibration of non-circular arches with rotatory inertia and shear deformation. International Journal of Solids and Structures, 37, 4871–4891 (2000)

    Article  Google Scholar 

  29. YANG, F., SEDAGHATI, R., and ESMAILZADEH, E. Free in-plane vibration of general curved beams using finite element method. Journal of Sound and Vibration, 318, 850–867 (2008)

    Article  Google Scholar 

  30. HUYNH, T. A., LUU, A. T., and LEE, J. Bending, buckling and free vibration analyses of functionally graded curved beams with variable curvatures using isogeometric approach. Meccanica, 52, 2527–2546 (2017)

    Article  MathSciNet  Google Scholar 

  31. MALEKZADEH, P., ATASHI, M. M., and KARAMI, G. In-plane free vibration of functionally graded circular arches with temperature-dependent properties under thermal environment. Journal of Sound and Vibration, 326, 837–851 (2009)

    Article  Google Scholar 

  32. HUGHES, T. J. R., COTTRELL, J. A., and BAZILEVS, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39-41), 4135–4195 (2005)

    Article  MathSciNet  Google Scholar 

  33. PIEGL, L. A. and TILLER, W. The NURBS Book, Springer, Berlin (1995)

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China

    Zhiwei Zhou & Meixia Chen

  2. College of Engineering, Huazhong Agricultural University, Wuhan, 430070, China

    Kun Xie

Authors
  1. Zhiwei Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Meixia Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kun Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Meixia Chen.

Additional information

Project supported by the National Natural Science Foundation of China (Nos. 51779098 and 51909098) and the Natural Science Foundation of Hubei Province of China (No. 2019CFB132)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, Z., Chen, M. & Xie, K. Non-uniform rational B-spline based free vibration analysis of axially functionally graded tapered Timoshenko curved beams. Appl. Math. Mech.-Engl. Ed. 41, 567–586 (2020). https://doi.org/10.1007/s10483-020-2594-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-020-2594-7

Keywords

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation