Skip to main content
SpringerLink
Log in

Jeffery-Hamel flow of non-Newtonian fluid with nonlinear viscosity and wall friction

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

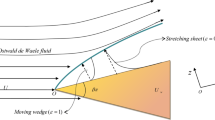
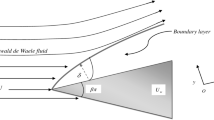
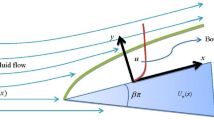
A Jeffery-Hamel (J-H) flow model of the non-Newtonian fluid type inside a convergent wedge (inclined walls) with a wall friction is derived by a nonlinear ordinary differential equation with appropriate boundary conditions based on similarity relationships. Unlike the usual power law model, this paper develops nonlinear viscosity based only on a tangential coordinate function due to the radial geometry shape. Two kinds of solutions are developed, i.e., analytical and semi-analytical (numerical) solutions with suitable assumptions. As a result of the parametric examination, it has been found that the Newtonian normalized velocity gradually decreases with the tangential direction progress. Also, an increase in the friction coefficient leads to a decrease in the normalized Newtonian velocity profile values. However, an increase in the Reynolds number causes an increase in the normalized velocity function values. Additionally, for the small values of wedge semi-angle, the present solutions are in good agreement with the previous results in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Rosenhead, L. The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proceedings of the Royal Society of London Series A, Mathematical and Physical Sciences, 175, 436–467 (1940)

    Article  MATH  Google Scholar 

  2. Tanner, R. I. Non-Newtonian fluid parameter estimation using conical flows. Industrial and Engineering Chemistry Fundamentals, 5, 55–59 (1966)

    Article  Google Scholar 

  3. Tadmor, Z. Non-Newtonian tangential flow in cylindrical annuli IV. Polymer Engineering and Science, 6, 203–212 (1966)

    Article  Google Scholar 

  4. Moffatt, H. K., Hooper, A., and Duffy, B. R. Flow of non-uniform viscosity in converging and diverging channels. Journal of Fluid Mechanics, 117, 283–304 (1982)

    Article  MATH  Google Scholar 

  5. Hull, A. M. and Pearson, J. R. A. On the converging flow of viscoelastic fluids through cones and wedges. Journal of Non-Newtonian Fluid Mechanics, 14, 219–247 (1984)

    Article  MATH  Google Scholar 

  6. Durban, D. On generalized radial flow patterns of viscoplastic solids with some applications. International Journal of Mechanical Sciences, 28, 97–110 (1986)

    Article  MATH  Google Scholar 

  7. Brewster, M. E., Chapman, S. J., Fitt, A. D., and Please, C. P. Asymptotics of slow flow of very small exponent power-law shear-thinning fluids in a wedge. European Journal of Applied Mathematics, 6, 559–571 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bird, C., Breward, C. J. W., Dellar, P., Edwards, C. M., Kaouri, K., Richardson, G., and Wilson, S. K. Mathematical modeling of pipe-flow and extrusion of composite materials. European Study Group with Industry, Unilever Research, Lancaster, UK, G1–G16 (2002)

    Google Scholar 

  9. Voropayev, S. I., Smirnov, S. A., and Testik, F. Y. On the case when steady converging/diverging flow of a non-Newtonian fluid in a round cone permits an exact solution. Mechanics Research Communications, 31, 477–482 (2004)

    Article  MATH  Google Scholar 

  10. Rahimi, S., Durban, D., and Khosid, S. Wall friction effects and viscosity reduction of gel propellants in conical extrusion. Journal of Non-Newtonian Fluid Mechanics, 165, 782–792 (2010)

    Article  MATH  Google Scholar 

  11. Nofal, T. A. An approximation of the analytical solution of the Jeffery-Hamel flow by homotopy analysis method. Applied Mathematical Sciences, 5, 2603–2615 (1970)

    MathSciNet  MATH  Google Scholar 

  12. Girishwar, N. Tangential velocity profile for axial flow through two concentric rotating cylinders with radial magnetic field. Defence Science Journal, 20, 207–212 (1970)

    MATH  Google Scholar 

  13. Timol, M. G. and Timol, A. G. Three-dimensional magnetofluiddynamic flow with pressure gradient and fluid injection. Journal of Engineering Mathematics, 19, 208–216 (1988)

    MATH  Google Scholar 

  14. Makinde, O. D. and Mhone, P. Y. Temporal stability of small disturbances in MHD Jeffery-Hamel flows. Computers and Mathematics with Applications, 53, 128–136 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Sadeghy, K., Khabazi, N., and Taghavi, S. M. Magnetohydrodynamic (MHD) flows of viscoelastic fluids in converging/diverging channels. International Journal of Engineering Science, 45, 923–938 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  16. Makinde, O. D., Bég, O. A., and Takhar, H. S. Magnetohydrodynamic viscous flow in a rotating porous medium cylindrical annulus with an applied radial magnetic field. International Journal of Applied Mathematics and Mechanics, 5, 68–81 (2009)

    Google Scholar 

  17. Alam, M. S. and Khan, M. A. H. Critical behviour of the MHD flow in convergent-divergent channels. Journal of Naval Architecture and Marine Engineering, 7, 83–93 (2010)

    Google Scholar 

  18. Shrama, P. R. and Singh, G. Steady MHD natural convection flow with variable electrical conductivity and heat generation along an isothermal vertical plate. Tamkang Journal of Science and Engineering, 13, 235–242 (2010)

    Google Scholar 

  19. Dib, A., Haiahem, A., and Bou-Said, B. An analytical solution of the MHD Jeffery-Hamel flow by the modified adomian decomposition method. Computers and Fluids, 102, 111–115 (2014)

    Article  MathSciNet  Google Scholar 

  20. Hayat, T., Abbasi, F. M., Ahmad, B., and Alsaedi, A. MHD mixed convection peristaltic flow with variable viscosity and thermal conductivity. Sains Malaysiana, 43, 1583–1590 (2014)

    Google Scholar 

  21. Usman, M., Naheed, Z., Nazir, A., and Mohyud-Din, S. T. On MHD flow of an incompressible viscous fluid. Journal of the Egyptian Mathematical Society, 22, 214–219 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Fogolari, F., Zuccato, P., Esposito, G., and Viglino, P. Biomolecular electrostatics with the linearized Poisson-Boltzmann equation. Biophysical Journal, 76, 1–16 (1999)

    Article  Google Scholar 

  23. Chen, C. H. and Santiago, J. G. A planar electroosmotic micropump. Journal of Microelectromechanical Systems, 11, 672–683 (2002)

    Article  Google Scholar 

  24. Berli, C. L. A. and Olivares, M. L. Electrokinetic flow of non-Newtonian fluids in microchannels. Journal of Colloid and Interface Science, 320, 582–589 (2008)

    Article  Google Scholar 

  25. Zhao, C., Zholkovskij, E., Masliyah, J. H., and Yang, C. Analysis of electroosmotic flow of powerlaw fluids in a slit microchannel. Journal of Colloid and Interface Science, 326, 503–510 (2008)

    Article  Google Scholar 

  26. Bohinc, K., Iglic A., and Slivnik, T. Linearized Poisson Boltzmann theory in cylindrical geometry. Elektrotehniski Vestnik, 75, 82–84 (2008)

    Google Scholar 

  27. Afonso, A. M., Alves, M. A., and Pinho, F. T. Analytical solution of mixed electroosmotic/pressure driven flows of viscoelastic fluids in microchannels. Journal of Non-Newtonian Fluid Mechanics, 159, 50–63 (2009)

    Article  MATH  Google Scholar 

  28. Ghosal, S. Mathematical modeling of electrokinetic effects in micro and nano fluidics. Microfluidics and Microfabrication (ed. Chakraborty, S.), Springer Science + Business Media, LLC, New York, 87–112 (2010)

    Google Scholar 

  29. Vasu, N. and De, S. Electroosmotic flow of power-law fluids at high zeta potentials. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 368, 44–52 (2010)

    Article  Google Scholar 

  30. Zhao, C. and Yang, C. An exact solution for electroosmosis of non-Newtonian fluids in microchannels. Journal of Non-Newtonian Fluid Mechanics, 166, 1076–1079 (2011)

    Article  MATH  Google Scholar 

  31. Sherwood, J. D., Mao, M., and Ghosal, S. Electroosmosis in a finite cylindrical pore: simple models of end effects. Langmuir, 30, 9261–9272 (2014)

    Article  Google Scholar 

  32. Bhattacharyya, K. and Layek, G. C. MHD boundary layer flow of dilatant fluid in a divergent channel with suction or blowing. Chinese Physics Letters, 28, 084705 (2011)

    Article  Google Scholar 

  33. Escandón, J. P., Santiago, F., and Bautista, O. E. Temperature distributions in a parallel flat plate microchannel with electroosmotic and magnetohydrodynamic micropumps. Proceedings of the 2013 International Conference on Mechanics, Fluids, Heat, Elasticity and Electromagnetic Fields, 177–181 (2013)

    Google Scholar 

  34. Escandón, J. P., Bautista, O. E., Santiago, F., and Méndez, F. Asymptotic analysis of non-Newtonian fluid flow in a microchannel under a combination of EO and MHD micropumps. Defect and Diffusion Forum, 348, 147–152 (2014)

    Article  Google Scholar 

  35. Nagler, J., Durban, D., and Khosid, S. On Planar Radial Flow with Non-Uniform Viscosity and Wall Friction Without Inertia Effect, M. Sc. dissertation, Technion-Israel Institute of Technology (2012)

    Google Scholar 

  36. Nagler, J. Laminar boundary layer model for power-law fluids with non-linear viscosity. WSEAS Transcations on Fluid Mechanics, 9, 19–25 (2014)

    Google Scholar 

  37. Nagler, J. Numerical and approximate solutions of boundary layer development due to a moving extensible surface. WSEAS Transcations on Fluid Mechanics, 10, 54–68 (2015)

    Google Scholar 

  38. Bird, R. B., Stewart, W. E., and Lightfoot, E. N. Transport Phenomena, John Wiley and Sons, New York (2001)

    Google Scholar 

  39. Landau, L. D. and Lifshitz, E. M. Fluid Mechanics, 2nd ed., Butterworth Heinemann, Oxford (1997)

    MATH  Google Scholar 

  40. Membrado, M. and Pacheco, A. F. Equations in curvilinear coordinates for fluids with nonconstant viscosity. Latin-American Journal of Physics Education, 5, 702–708 (2011)

    Google Scholar 

  41. Sherwood, J. D. and Durban, D. Squeeze flow of a power law viscoplastic solid. Journal of Non-Newtonian Fluid Mechanics, 62, 35–54 (1996)

    Article  Google Scholar 

  42. Kaylon, D. M., Yaras, P., Aral, B., and Yilmazer, U. Rheological behavior of a concentrated suspension: a solid rocket fuel simulant. Journal of Rheology, 37, 35–53 (1993)

    Article  Google Scholar 

  43. Barnes, H. A. A review of the slip (wall depletion) of polymer solution emulsions and particle suspensions in viscometers: its cause, character, and cure. Journal of Non-Newtonian Fluid Mechanics, 56, 225–251 (1995)

    Google Scholar 

  44. Nagler, J. Advanced Non-Newtonian and Nano Fluidics Flows, LAP Publishing, Germany, 83–91 (2016)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Fluid Mechanics and Heat Transfer, Faculty of Engineering, Tel-Aviv University, Ramat-Aviv, 69978, Israel

    J. Nagler

Authors
  1. J. Nagler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. Nagler.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nagler, J. Jeffery-Hamel flow of non-Newtonian fluid with nonlinear viscosity and wall friction. Appl. Math. Mech.-Engl. Ed. 38, 815–830 (2017). https://doi.org/10.1007/s10483-017-2206-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-017-2206-8

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation