Abstract
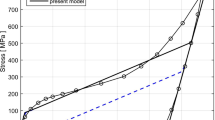
Shape memory alloys (SMAs) have been explored as smart materials and used as dampers, actuator elements, and smart sensors. An important character of SMAs is its ability to recover all of its large deformations in mechanical loading-unloading cycles without showing permanent deformation. This paper presents a stress-induced phenomenological constitutive equation for SMAs, which can be used to describe the superelastic hysteresis loops and phase transformation between Martensite and Austenite. The Martensite fraction of SMAs is assumed to be dependent on deviatoric stress tensor. Therefore, phase transformation of SMAs is volume preserving during the phase transformation. The model is implemented in large deformation finite element code and cast in the updated Lagrangian scheme. In order to use the Cauchy stress and the linear strain in constitutive laws, a frame indifferent stress objective rate has to be used. In this paper, the Jaumann stress rate is used. Results of the numerical experiments conducted in this study show that the superelastic hysteresis loops arising with the phase transformation can be effectively captured.
Similar content being viewed by others
References
Birman, V. Review of mechanics of shape memory alloy structures. Applied Mechanics Reviews 50, 629–645 (1998)
Duerig, T. W., Melton, K. N., Stockel, D., and Wayman, C. M. Engineering Aspects of Shape Memory Alloys, Butterworth-Heinemann, 137–148 (1990)
Lubliner, J. and Auricchio, F. Gerenalized plasticity and shape memory alloys. International Journal of Solids and Structures 33, 991–1003 (1996)
Auricchio, F., Taylor, R. L., and Lubliner, J. Shape-memory alloys: macromodelling and numerical simulations of the superelastic behavior. Comp. Meths. Appl. Mech. Engrg. 146, 281–312 (1997)
Barret, D. J. and Sullivan, B. J. A three-dimensional phase transformation model for shape memory alloys. J. Intel. Mater. Syst. Struct. 6, 831–839 (1995)
Brinson, L. C. and Lammering, R. Finite-element analysis of the behavior of shape memory alloys and their applications. International Journal of Solids and Structures 30, 3261–3280 (1993)
Qidwai, M. A. and Lagoudas, D. C. Numerical implementation of a shape memory alloy thermomechanical constitutive model using return mapping algorithms. International Journal of Numerical Methods in Engineering 47, 1123–1168 (2000)
Rengarajan, G., Kumar, R. K., and Reddy, J. N. Numerical modeling of stress induced martensitic phase transformations in shape memory alloys. International Journal of Solids and Structures 35, 1489–1513 (1998)
Tanaka, K., Nishimura, F., Hayashi, T., Tobushi, H., and Lexcellent, C. Phenomenological analysis on subloops and cyclic behavior in shape memory alloys under mechanical and/or thermal loads. Mechnica of Materials 19, 281–292 (1995)
Masud A., Panahandeh, M., and Aurrichio, F. Finite-strain finite element model for the pseudoelastic behavior of shape memory alloys. Comp. Meths. Appl. Mech. Engrg. 148, 23–37 (1997)
Auricchio, F. A robust integration-algorithm for a finite-strain shape memory alloy superelastic model. International Journal of Plasticity 17, 971–990 (2001)
Stein, E. and Sagar, G. Theory and finite element computation of cyclic martensitic phase transformation at finite strain. International Journal of Numerical Methods in Engineering 74, 1–31 (2008)
Masud, A. and Xia, K. A variational multiscale method for computational inelasticity: application to superelasticity in shape memory alloys. Comp. Meths. Appl. Mech. Engrg. 195, 4512–4531 (2006)
Hughes, T. J. R. and Winget, J. Finite rotation effects in numerical integration of rate constitutive equations arising in large-deformation analysis. International Journal of Numerical Methods in Engineering 33, 1413–1449 (1980)
Simo, J. C. and Hughes, T. J. R. Computational Inelasticity, Springer-Verlag, New York (1993)
Belytschko, T., Liu, W. K., and Moran, B. Nonlinear Finite Elements for Continua and Structures, John Wiley & Sons Ltd., New York (2000)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Xing-ming GUO
Rights and permissions
About this article
Cite this article
Xia, Km., Pan, Ty. & Liu, Sh. Three dimensional large deformation analysis of phase transformation in shape memory alloys. Appl. Math. Mech.-Engl. Ed. 31, 1261–1272 (2010). https://doi.org/10.1007/s10483-010-1359-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10483-010-1359-7