Skip to main content
SpringerLink
Log in

Numerical solutions of singular integral equations for planar rectangular interfacial crack in three dimensional bimaterials

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

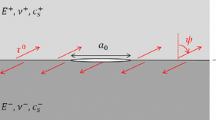
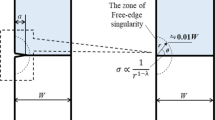
Stress intensity factors for a three dimensional rectangular interfacial crack were considered using the body force method. In the numerical calculations, unknown body force densities were approximated by the products of the fundamental densities and power series; here the fundamental densities are chosen to express singular stress fields due to an interface crack exactly. The calculation shows that the numerical results are satisfied. The stress intensity factors for a rectangular interface crack were indicated accurately with the varying aspect ratio, and bimaterial parameter.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Salganik R L. The brittle fracture of cemented bodies[J]. Prikl Mat Mekh, 1963, 27:957–962.

    Google Scholar 

  2. Erdogan F. Stresses distribution in a non-homogeneous elastic plane with crack[J]. J Appl Mech, 1963, 3(2):232–236.

    Google Scholar 

  3. England F. A crack between dissimilar media[J]. J Appl Mech, 1965, 32(3):400–402.

    Google Scholar 

  4. Rice J R, Sih G C. Plane problems of cracks in dissimilar media[J]. J Appl Mech, 1965, 32(3):418–423.

    Google Scholar 

  5. Comninou M. The interface crack[J]. J Appl Mech, 1977, 44(4):631–636.

    MATH  Google Scholar 

  6. Noda N A, Oda K. Interaction effect of stress intensity factors for any number of collinear interface cracks[J]. Int J of Fract, 1997, 84(2):117–128.

    Article  Google Scholar 

  7. Willis J R. Fracture mechanics of interfacial crack[J]. J Mech Phys Solids, 1971, 19(6):353–368.

    Article  MATH  Google Scholar 

  8. Tucker M O. In two-phase solids under longitudinal shear loading[J]. Int. J Fract, 1974, 10(3):323–336.

    Article  Google Scholar 

  9. England F, Gupta G D. Bonded wedges with an interface crack under anti-plane shear loading[J]. Int J Fract, 1975, 11(4):583–593.

    Article  Google Scholar 

  10. Willis J R. The penny-shaped crack on an interface[J]. J Mech Appl Math, 1972, 25(2):367–385.

    Article  MATH  Google Scholar 

  11. Mossakovski V I, Rybka M T. Generalization of the griffith-senddon criterion for the case of a non-homogeneous body[J]. Prikl Mat Mekh, 1964, 28:1061–1069.

    Google Scholar 

  12. England F. Stress distribution in bonded dissimilar materials containing circular or ring-shaped cavities[J]. Trans ASME, Ser E, J Appl Mech, 1965, 32(4):829–836.

    Google Scholar 

  13. Kassir M K, Bregman A M. The stress intensity factor for a penny-shaped crack between two dissimilar materials[J]. Trans ASME, Ser E, J Appl Mech, 1972, 39(1):308–310.

    Google Scholar 

  14. Lowengrub M, Senddon I N. The effect of internal pressure on a penny-shaped crack at the interface of two bonded dissimilar elastic half-spaces[J]. Int J Engng Sci, 1974, 12(5):387–396.

    Article  Google Scholar 

  15. Shibuya T, Koizumi T, Iwamoto T. Stress analysis of the vicinity of an elliptical crack at the interface of two bonded half-spaces[J]. JSME Int J, 1989, 32:485–491.

    Google Scholar 

  16. Noda N A, Kakita M, Chen M C. Analysis of stress intensity factors of a ring-shaped interface crack[J]. Int J of Solids and Struct, 2003, 40(24):6577–6592.

    Article  MATH  Google Scholar 

  17. Wang Q, Noda N A. Variation of stress intensity factors along the front of 3D rectangular crack by using a singular integral equation method[J]. Int J of Fracture, 2001, 108(2):119–131.

    Article  Google Scholar 

  18. Chen M C, Noda N A, Tang R J. Application of finite-part integrals to planar interfacial fracture problems in three dimensional bimaterials[J]. J Appl Mech, 1999, 66(6):885–890.

    Google Scholar 

  19. Qin T Y, Noda N A. Stress intensity factors of rectangular crack meeting a bimateral interface[J]. Int J of Solids and Struct, 2003, 40(10):2473–2486.

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Science, China Agricultural University, Beijing, 100083, P. R. China

    Xu Chun-hui  (徐春晖) & Qin Tai-yan  (秦太验) (Associate Professor, Doctor)

  2. Department of Mechanical Engineering, Kyushu Institute of Technology, Kitakyushu, 804-8550, Japan

    Nao-Aki Noda  (野田尚昭)

Authors
  1. Xu Chun-hui  (徐春晖)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qin Tai-yan  (秦太验)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nao-Aki Noda  (野田尚昭)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qin Tai-yan  (秦太验).

Additional information

Communicated by WANG Yin-bang

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xu, Ch., Qin, Ty. & Noda, NA. Numerical solutions of singular integral equations for planar rectangular interfacial crack in three dimensional bimaterials. Appl Math Mech 28, 751–757 (2007). https://doi.org/10.1007/s10483-007-0605-y

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-007-0605-y

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation