Abstract
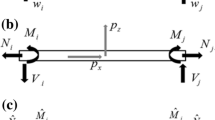
Beams and plates manufactured from laminates of composite materials have distinct advantages in a significant number of applications. However, the anisotropy arising from these materials adds a significant degree of complexity, and thus time, to the stress and deformation analyses of such components, even using numerical approaches such as finite elements. The analysis of composite laminate beams subjected to uniform extension, bending, and/or twisting loads was performed by a novel implementation of the usual finite element method. Due to the symmetric features of the deformations, only a thin slice of the beam to be analysed needs to be modelled. Conventional three-dimensional solid finite elements were used for the structural discretization. The accurate deformation relationships were formulated and implemented through the coupling of nodal translational degrees of freedom in the numerical analysis. A sample solution for a rectangular composite laminate beam is presented to show the validity and accuracy of the proposed method.
Similar content being viewed by others
References
Pipes R B, Pagano N J. Interlaminar stresses in composite laminates under uniform axial extension[J]. Journal of Composite Materials, 1970, 4:538–548.
Altus E, Rotem A, Shmueli M. Free edge effect in angle ply laminates—a new three dimensional finite difference solution[J]. Journal of Composite Materials, 1980, 14(1):21–30.
Davi G, Milazzo A. Boundary integral formulation for composite laminates in torsion[J]. AIAA Journal, 1997, 35(10):1660–1666.
Ye L. Some characteristics of distributions of free-edge interlaminar stresses in composite laminates[J]. International Journal of Solids and Structures, 1990, 26(3):331–351.
Mitchell J A, Reddy J N. Study of interlaminar stresses in composite laminates subjected to torsional loading [J]. AIAA Journal, 2001, 39(7):1374–1382.
Wang S S, Choi I. Boundary-layer effects in composite laminates: Part 2, free-edge stress solutions and basic characteristics[J]. ASME Journal of Applied Mechanics, 1982, 49(3):549–560.
Pagano N J. Stress fields in composite laminates[J]. International Journal of Solids and Structures, 1978, 14(5):385–400.
Pagano N J. Free edge stress fields in composite laminates[J]. International Journal of Solids and Structures, 1978, 14(5):401–406.
Yin W L. Free-edge effects in anisotropic laminates under extension, bending and twisting, Part I: a stress-function-based variational approach[J]. ASME Journal of Applied Mechanics, 1994, 61(2):410–415.
Jiang W G. The Development of the Helically Symmetric Boundary Condition in Finite Element Analysis and Its Applications to Spiral Strands[D]. PhD Dissertation, Brunel University, Uxbridge, 1999.
Jiang W G, Henshall J L. The development and applications of the helically symmetric boundary conditions in finite element analysis[J]. Communications in Numerical Methods in Engineering, 1999, 15(6):435–443.
Jiang W G, Henshall J L. A novel finite element model for helical springs[J]. Finite Elements in Analysis and Design, 2000, 35(4):363–377.
Jiang W G, Henshall J L. Torsion-extension coupling in initially twisted beams by finite elements[J]. European Journal of Mechanics A-Solids, 2001, 20(3):501–508.
Jiang W G, Henshall J L, Walton J M. A concise finite element model for 3-layered straight wire rope strand[J]. International Journal of Mechanical Sciences, 2000, 42(1):63–86.
Jiang W G, Yao M S, Walton J M. A concise finite element model for simple wire rope strand[J]. International Journal of Mechanical Sciences, 1999, 41(2):143–161.
Jiang W G, Henshall J L. A coupling cross-section finite element model for torsion analysis of prismatic bars[J]. European Journal of Mechanics A-Solids, 2002, 21(3):513–522.
Lekhnitskii S G. Theory of Elasticity of an Anisotropic Elastic Body[M]. Holden-Day, Inc, Uxbridge, 1963.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by FU Ming-fu
Rights and permissions
About this article
Cite this article
Jiang, Wg., Henshall, J.L. Analysis of composite laminate beams using coupling cross-section finite element method. Appl Math Mech 27, 1709–1718 (2006). https://doi.org/10.1007/s10483-006-1213-z
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s10483-006-1213-z