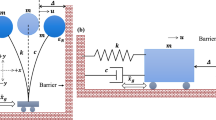
Abstract
The objective is to present exact analytical solutions of longitudinal impact analysis for slender conical rods struck by a particle and a new method is proposed for conical rod-particle impact analysis, in which the superposition method is used and the response of the rod is presented. These analytical results are exact and can be used to validate the numerical methods or other analytical results. The numerical example shows that one of the advantages of the present method is that the analytical form is very simple. The result is that mass ratio and some variables describing the geometrical shape of rods such as taper, length and radius play an important role in impact dynamic system.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Goldsmith W. Impact: the Theory and Physical Behaviour of Colliding Solids[M]. Edward Arnold Ltd, London, 1960.
Graff K F. Wave Motion in Elastical Solids[M]. Clarendon, Oxford, 1975.
Hu B, Eberhard P, Schiehlen W. Symbolic impact analysis for a falling conical rod against the rigid ground[J]. Journal of Sound and Vibration, 2001, 240(1):41–57.
Hu Bin, Eberhard Peter. Symbolic computation of longitudinal impact wave[J]. Comput Methods Appl Mech Engrg, 2001, 190(3):4805–4815.
Timoshenko S. Vibration Problems in Engineering[M]. 2nd Ed. Van Nostrand, New York, 1937.
Sankzn, Yuganva. Longitudinal vibrations of elastic rods of stepwise-variable cross-section colliding with a rigid obstacle[J]. J Appl Maths Mechs, 2001, 65(3):427–433.
Zhu Dechao, Xing Yufeng. Analytical solution of point elastic impact between structures[J]. Acta Mechanica Sinica, 1996, 28(1):99–103 (in Chinese).
Zhu Dechao, Xing Yufeng. Analytical solution of impact problems of rod structures with springs[J]. Comput Methods Appl Mech Engrg, 1998, 160(2):315–323.
Abrate S. Vibration of non-uniform rods and beams[J]. Journal of Sound and Vibration, 1995, 185(4):703–786.
Kumar B M, Sujith R. Exact solutions for the longitudinal vibration of non-uniform rods[J]. Journal of Sound and Vibration, 1997, 207(5):721–729.
Anindya Chatterjee. The short-time impulse response of Euler-Bernoulli beams[J]. ASME Journal of Applied Mechanics, 2004, 71(3):208–218.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by YUE Zhu-feng
Project supported by the National Natural Science Foundation of China (Nos.10372084 and 10572119); Program for New Century Excellent Talents of Education Ministry of China (No.NCET-04-0958) and the Open Foundation of State Key Laboratory of Structural Analysis of Industrial Equipment
Rights and permissions
About this article
Cite this article
Bao, Sy., Deng, Zc. Analytical solutions for response of collision of particle with conical rod caused by longitudinal vibration. Appl Math Mech 27, 927–934 (2006). https://doi.org/10.1007/s10483-006-0708-z
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s10483-006-0708-z