Skip to main content
SpringerLink
Log in

Estimation of player aging curves using regression and imputation

  • Original Research
  • Published:
Annals of Operations Research Aims and scope Submit manuscript

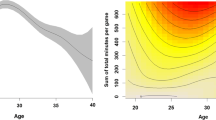
Abstract

The impact of age on performance is a fundamental component to models of player valuation and prediction across sport. Age effects are typically measured using age curves, which reflect the expected average performance at each age among all players that are eligible to participate. Most age curve methods, however, ignore the reality that age likewise influences which players receive opportunities to perform. In this paper we begin by highlighting how selection bias is linked to the ages in which we observe players perform. Next, using underlying distributions of how players move in and out of sport organizations, we assess the performance of various methods for age curve estimation under the selection bias of player entry and issues of small samples at younger and older ages. We propose several methods for player age curve estimation, introduce a missing data framework, and compare these new methods to more familiar approaches including both parametric and semi-parametric modeling. We then use simulations to compare several approaches for estimating aging curves. Imputation-based methods, as well as models that account for individual player skill, tend to generate lower root mean squared error (RMSE) and age curve shapes that better match the truth. We implement our approach using data from the National Hockey League. All of the data and code for this paper are available in a Github repository.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. MLB stands for Major League Baseball and NBA stands for National Basketball League

  2. Imputation with truncation limits the range of values that generated realizations can take. For example, if \(X \sim N(0,1)\) is truncated below at \(-2\) then the realized values of X could only take values in \((-2,\infty )\) whereas untruncated realizations could take values in \((-\infty , \infty )\).

References

  • Albert, J. (2002). Smoothing career trajectories of baseball hitters. Unpublished manuscript, Bowling Green State University, at bayes. bgsu. edu/papers/career_trajectory. pdf

  • Berry, S. M., Reese, C. S., & Larkey, P. D. (1999). Bridging different eras in sports. Journal of the American Statistical Association, 94(447), 661–676.

    Article  Google Scholar 

  • Bradbury, J. C. (2009). Peak athletic performance and ageing: evidence from baseball. Journal of Sports Sciences, 27(6), 599–610.

    Article  Google Scholar 

  • Brander, J. A., Egan, E. J., & Yeung, L. (2014). Estimating the effects of age on nhl player performance. Journal of Quantitative Analysis in Sports, 10(2), 241–259.

    Article  Google Scholar 

  • Fair, R.C. (2008). Estimated age effects in baseball. Journal of Quantitative Analysis in Sports 4(1).

  • Judge, J. (2020a). An approach to survivor bias in baseball. Baseball Prospectus (https://www.baseballprospectus.com/news/article/59491/an-approach-to-survivor-bias-in-baseball/).

  • Judge, J. (2020b). The delta method, revisited: Rethinking aging curves. Baseball Prospectus (https://www.baseballprospectus.com/news/article/59972/the-delta-method-revisited/).

  • Kovalchik, S. A., & Stefani, R. (2013). Longitudinal analyses of olympic athletics and swimming events find no gender gap in performance improvement. Journal of Quantitative Analysis in Sports, 9(1), 15–24.

    Article  Google Scholar 

  • Lailvaux, S. P., Wilson, R., & Kasumovic, M. M. (2014). Trait compensation and sex-specific aging of performance in male and female professional basketball players. Evolution, 68(5), 1523–1532.

    Article  Google Scholar 

  • Lichtman, M. (2009). How do baseball players age. Fan Graphs (https://tht.fangraphs.com/how-do-baseball-players-age-part-2/).

  • Paparrizos, J., Gravano, L. (2015). k-shape: Efficient and accurate clustering of time series. In: Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, pp. 1855–1870.

  • R Development Core Team (2007). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org. ISBN 3-900051-07-0

  • Schulz, R., Musa, D., Staszewski, J., & Siegler, R. S. (1994). The relationship between age and major league baseball performance: Implications for development. Psychology and aging, 9(2), 274.

    Article  Google Scholar 

  • Tulsky, E. (2014). How shot attempt differential changes with age. https://www.sbnation.com/nhl/2014/3/20/5528472/nhl-stats-corsi-vs-age.

  • Turtoro, C. (2019). Flexible aging in the nhl using gam. https://rpubs.com/cjtdevil/nhl_aging.

  • Vaci, N., Cocić, D., Gula, B., & Bilalić, M. (2019). Large data and bayesian modeling-aging curves of nba players. Behavior research methods, 51(4), 1544–1564.

    Article  Google Scholar 

  • Villaroel, C., Mora, R., & Gonzalez-Parra, G. C. (2011). Elite triathlete performance related to age. Journal of Human Sport and Exercise, 6(2), 363–373.

    Article  Google Scholar 

  • Wakim, A., Jin, J. (2014). Functional data analysis of aging curves in sports. arXiv preprint arXiv:1403.7548.

Download references

Acknowledgements

We would like to thank CJ Turturo for making his code available.

Author information

Authors and Affiliations

  1. St. Lawrence University, Canton, NY, USA

    Michael Schuckers

  2. National Football League, New York, USA

    Michael Lopez

  3. Yale University, New Haven, USA

    Brian Macdonald

Authors
  1. Michael Schuckers
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Lopez
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Brian Macdonald
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael Schuckers.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This material is based upon work supported by the U.S. National Science Foundation under Grant No. CNS-1919554.

Appendix

Appendix

Below is a table highlighting average RMSE for different simulation settings, by age.

Fig. 10
figure 10

Average Root Mean Squared Error by Age (column), Method (row), and number of players (sets of rows) across simulations

Full size image

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schuckers, M., Lopez, M. & Macdonald, B. Estimation of player aging curves using regression and imputation. Ann Oper Res 325, 681–699 (2023). https://doi.org/10.1007/s10479-022-05127-y

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-022-05127-y

Keywords

Search

Navigation