Abstract
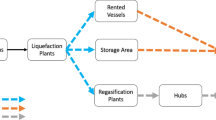
The security of gas supply is a crucially important question for the economy of any country. South-eastern Australia has a sophisticated network of gas pipelines that connect the production sites on the ocean shelf and in the inner part of the continent with the major consumers, which are the state capital cities (Adelaide, Melbourne, Hobart, Sydney and Brisbane) and the regional industrial town of Gladstone. Two optimization models were developed in order to test the security of the gas supply system against possible global impacts that affect the demand for natural gas. The modeling research in the present work was focused on the simulation of delivery when demands reach their peak values. The first model minimizes squares of shortfalls in major supply nodes. As major constraints the models used the production levels, supply capacities and the mass balance in pipe junctions. The second model minimizes the total cost of gas delivery, which is a sum of production and transportation costs, while the constraints stay the same. Both models were run for a series of plausible economic scenarios which generated the future values of demand. The potential “bottle necks” in the system components were identified. It was found that the first constraint which became scarce is the pipe providing gas to the port of Gladstone. The capacity of this pipe should be increased in order to meet growing demand. Gladstone is also the site of the liquefied natural gas export industry on the east coast. An increase in pipeline capacity will facilitate the increase of export from Gladstone, but will reduce supply to other consumption nodes. A sensitivity analysis (SA) was implemented for both formulations of the model. The objective was to examine how the key indicators of system security and pipeline flow were impacted by changes (increase and decrease) in peak demands. For this analysis the predicted annual scenarios for peak demand increase for four states (ACT was treated as part of NSW in the present work) were used. For the analysis of the decrease of demand, proportional changes of the same magnitude in demand were used for all demand nodes. It can be concluded that with the current infrastructure the most vulnerable components of the system are industrial gas users in Gladstone and Mt. Isa, whereas amongst the domestic consumers it is Brisbane. This conclusion can be utilized in further decisions on pipeline infrastructure upgrades.





Similar content being viewed by others
References
Alvey, T., Goodwin, D., Ma, X., Streifert, D., & Sun, D. (1998). A security-constraint bid-clearing system for the New Zealand wholesale electricity market. IEEE Transactions on Power Systems, 13(2), 340–346.
Australian Energy Market Operator—AEMO. (2010). Gas statement opportunities of Eastern and South Eastern Australia. Executive briefing, Melbourne (p. 36).
Australian Energy Market Operator—AEMO. (2012). 2012 Gas statement of opportunities for Eastern and South Eastern Australia Melbourne.
Babonneau, F., Nesterov, Y., & Vial, J. (2012). Design and operations of gas transmission networks. Operations Research, 60(1), 34.
Contesse, L., Ferrer, J.-C., & Maturana, S. (2005). A mixed-integer programming model for gas purchase and transportation. Annals of Operations Research, 139(1), 39–63.
Egging, R., Gabriel, S. A., Holz, F., & Zhuang, J. (2008). A complementarity model for the European natural gas market. Energy Policy, 36(7), 2385–2414.
Egging, R., Holz, F., & Gabriel, S. A. (2010). The world gas model—a multi-period mixed complementary model for the global natural gas market. Energy, 35(10), 4016–4029.
Gabriel, S. A., Zhuang, J., & Kiet, S. (2005). A large-scale linear complementarity model of the North American natural gas market. Energy Economics, 27(4), 639–665.
Halovsen-Weare, E. E., & Fagerholt, K. (2013). Routing and scheduling in a liquefied natural gas shipping problem with inventory and berth constraints. Annals of Operations Research, 203(1), 167–186.
Hellemo, L., Midthun, K. T., Tomasgard, A., & Werner, A. (2012). Natural gas infrastructure design with an operational perspective. Energy Procedia, 26, 67–73.
Hellemo, L., Midthun, K. T., Tomasgard, A., & Werner, A. (2013). Multi-stage stochastic programming for natural gas infrastructure design with a production perspective. In Stochastic programming: Applications in finance, energy, planning and logistics. World Scientific 2013, ISBN 978-9814407502 (pp. 259–288).
Kabirian, A., & Hemmati, M. R. (2007). A strategic planning model for natural gas transmission networks. Energy Policy, 35(11), 5656–5670.
Kolb, O., Lang, J., & Bales, P. (2007). Adaptive linearized models for optimization of gas networks. PAMM, 7(1), 1061301–1061302.
Li, X., Armagan, E., Tomasgard, A., & Barton, P. I. (2011). Stochastic pooling problem for natural gas production network design and operation under uncertainty. AIChE Journal, 57(8), 2120–2135.
Mahlke, D., Martin, A., & Moritz, S. (2010). A mixed integer approach for time-dependent gas network optimization. Optimization Methods & Software, 25(4), 625–644.
Nygreen, B., Christiansen, M., Haugen, K., Bjørkvoll, T., & Kristiansen, Ø. (1998). Modelling Norwegian petroleum production and transportation. Annals of Operations Research, 82(0), 251–267.
Najibi, H., & Taghavi, N. (2011). Effect of different parameters on optimum design for high pressure natural gas trunk-lines. Journal of Natural Gas Science and Engineering, 3(4), 547–554.
Pepper, W., Ring, B. J., Read, E. G., & Starkey, S. R. (2012). Implementation of a scheduling and pricing model for natural gas. In A. Sorokin, S. Rebennack, & P. M. Pardalos (Eds.), Handbook of networks in power systems II (pp. 3–35). Berlin: Springer.
Read, E. G., Ring, B. J., Starkey, S. R., & Pepper, W. (2012). An LP based market design for natural gas. In A. Sorokin, S. Rebennack, & P. M. Pardalos (Eds.), Handbook of networks in power systems II (pp. 77–113). Berlin: Springer.
Rios-Mercado, R. Z. (2002). Natural gas pipeline optimization. In P. M. Pardalos & M. G. C. Resende (Eds.), Handbook of applied optimization (pp. 813–826). New York: Oxford University Press.
Rios-Mercado, R. Z., Wu, S., Scott, L. R., & Boyd, E. A. (2002). A reduction technique for natural gas transmission network optimization problems. Annals of Operations Research, 117(1), 217–234.
Rios-Mercado, R. Z., Kim, S., & Boyd, E. A. (2006). Efficient operation of natural gas transmission systems: A network-based heuristic for cyclic structures. Computers and Operations Research, 33(8), 2323–2351.
Ruan, Y., Liu, Q., Zhou, W., Batty, B., Gao, W., Ren, J., et al. (2009). A procedure to design the mainline system in natural gas networks. Applied Mathematical Modeling, 33(7), 3040–3051.
Steinbach, M. C. (2007). On PDE solution in transient optimization of gas networks. Journal of Computational and Applied Mathematics, 203(2), 345–361.
Tomasgard, A., Rømo, F., Fodstad, M., & Midthun, K. T. (2007). Optimization models for the natural gas value chain. I. In Geometric modelling, numerical simulation, and optimization: Applied mathematics at SINTEF. Springer Science+Business Media B.V., ISBN 978-3-540-68782-5 (pp. 521–558).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Schreider, S., Plummer, J., McInnes, D. et al. Sensitivity analysis of gas supply optimization models. Ann Oper Res 226, 565–588 (2015). https://doi.org/10.1007/s10479-014-1709-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-014-1709-0