Skip to main content
SpringerLink
Log in

Rectilinear distance to a facility in the presence of a square barrier

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

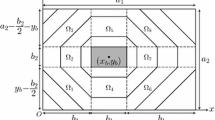
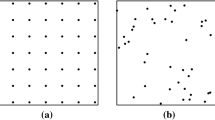
This paper derives analytical expressions for the rectilinear distance to a facility in the presence of a square barrier. The distribution of the barrier distance is derived for two regular patterns of facilities: square and diamond lattices. This distribution, which provides all the information about the barrier distance, will be useful for facility location problems with barriers and reliability analysis of facility location. The distribution of the barrier distance demonstrates how the location and the size of the barrier affect the barrier distance. A numerical example shows that the total barrier distance increases as the barrier gets closer to a facility, whereas the maximum barrier distance increases as the barrier becomes greater in size.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  • Aneja, Y., & Parlar, M. (1994). Algorithms for Weber facility location in the presence of forbidden regions and/or barriers to travel. Transportation Science, 28, 70–76.

    Article  Google Scholar 

  • Batta, R., Ghose, A., & Palekar, U. (1989). Locating facilities on the Manhattan metric with arbitrarily shaped barriers and convex forbidden regions. Transportation Science, 23, 26–36.

    Article  Google Scholar 

  • Bell, M., & Iida, Y. (2003). The network reliability of transport. Oxford: Pergamon.

    Google Scholar 

  • Bischoff, M., & Klamroth, K. (2007). An efficient solution method for Weber problems with barriers based on genetic algorithms. European Journal of Operational Research, 177, 22–41.

    Article  Google Scholar 

  • Bischoff, M., Fleischmann, T., & Klamroth, K. (2009). The multi-facility location-allocation problem with polyhedral barriers. Computers & Operations Research, 36, 1376–1392.

    Article  Google Scholar 

  • Butt, S., & Cavalier, T. (1996). An efficient algorithm for facility location in the presence of forbidden regions. European Journal of Operational Research, 90, 56–70.

    Article  Google Scholar 

  • Canbolat, M., & Wesolowsky, G. (2010). The rectilinear distance Weber problem in the presence of a probabilistic line barrier. European Journal of Operational Research, 202, 114–121.

    Article  Google Scholar 

  • Dearing, P., Hamacher, H., & Klamroth, K. (2002). Dominating sets for rectilinear center location problems with polyhedral barriers. Naval Research Logistics, 49, 647–665.

    Article  Google Scholar 

  • Dearing, P., Klamroth, K., & Segars, R. Jr. (2005). Planar location problems with block distance and barriers. Annals of Operations Research, 136, 117–143.

    Article  Google Scholar 

  • Dearing, P., & Segars, R. Jr. (2002a). An equivalence result for single facility planar location problems with rectilinear distance and barriers. Annals of Operations Research, 111, 89–110.

    Article  Google Scholar 

  • Dearing, P., & Segars, R. bsuffixJr. (2002b). Solving rectilinear planar location problems with barriers by a polynomial partitioning. Annals of Operations Research, 111, 111–133.

    Article  Google Scholar 

  • Frieß, L., Klamroth, K., & Sprau, M. (2005). A wavefront approach to center location problems with barriers. Annals of Operations Research, 136, 35–48.

    Article  Google Scholar 

  • Hamacher, H., & Klamroth, K. (2000). Planar Weber location problems with barriers and block norms. Annals of Operations Research, 96, 191–208.

    Article  Google Scholar 

  • Katz, I., & Cooper, L. (1981). Facility location in the presence of forbidden regions, I: Formulation and the case of Euclidean distance with one forbidden circle. European Journal of Operational Research, 6, 166–173.

    Article  Google Scholar 

  • Klamroth, K. (2001a). Planar Weber location problems with line barriers. Optimization, 49, 517–527.

    Article  Google Scholar 

  • Klamroth, K. (2001b). A reduction result for location problems with polyhedral barriers. European Journal of Operational Research, 130, 486–497.

    Article  Google Scholar 

  • Klamroth, K. (2002). Single-facility location problems with barriers. New York: Springer.

    Google Scholar 

  • Klamroth, K. (2004). Algebraic properties of location problems with one circular barrier. European Journal of Operational Research, 154, 20–35.

    Article  Google Scholar 

  • Krause, E. (1987). Taxicab geometry: an adventure in non-Euclidean geometry. New York: Dover.

    Google Scholar 

  • Larson, R., & Li, V. (1981). Finding minimum rectilinear distance paths in the presence of barriers. Networks, 11, 285–304.

    Article  Google Scholar 

  • Larson, R., & Odoni, A. (1981). Urban operations research. Englewood Cliffs: Prentice-Hall.

    Google Scholar 

  • Larson, R., & Sadiq, G. (1983). Facility locations with the Manhattan metric in the presence of barriers to travel. Operations Research, 31, 652–669.

    Article  Google Scholar 

  • McGarvey, R., & Cavalier, T. (2003). A global optimal approach to facility location in the presence of forbidden regions. Computers & Industrial Engineering, 45, 1–15.

    Article  Google Scholar 

  • Mitchell, J. (1992). l 1 shortest paths among polygonal obstacles in the plane. Algorithmica, 8, 55–88.

    Article  Google Scholar 

  • Miyagawa, M. (2005). Evaluation of the damage caused by facility closing and road blockades from increase in travel distances. Journal of the City Planning Institute of Japan, 40, 187–192. (In Japanese).

    Google Scholar 

  • Miyagawa, M. (2008). Analysis of facility location using ordered rectilinear distance in regular point patterns. FORMA, 23, 89–95.

    Google Scholar 

  • Nandikonda, P., Batta, R., & Nagi, R. (2003). Locating a 1-center on a Manhattan plane with “arbitrarily” shaped barriers. Annals of Operations Research, 123, 157–172.

    Article  Google Scholar 

  • Sarkar, A., Batta, R., & Nagi, R. (2007). Placing a finite size facility with a center objective on a rectangular plane with barriers. European Journal of Operational Research, 179, 1160–1176.

    Article  Google Scholar 

  • Savaş, S., Batta, R., & Nagi, R. (2002). Finite-size facility placement in the presence of barriers to rectilinear travel. Operations Research, 50, 1018–1031.

    Article  Google Scholar 

  • Viegas, J., & Hansen, P. (1985). Finding shortest paths in the plane in the presence of barriers to travel (for any l p -norm). European Journal of Operational Research, 20, 373–381.

    Article  Google Scholar 

  • Wang, S., Bhadury, J., & Nagi, R. (2002). Supply facility and input/output point locations in the presence of barriers. Computers & Operations Research, 29, 685–699.

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by Grant-in-Aid for Young Scientists (B) (22710140). I am grateful to two anonymous reviewers for helpful comments and suggestions.

Author information

Authors and Affiliations

  1. Department of Ecosocial System Engineering, University of Yamanashi, 4-3-11 Takeda, Kofu, Yamanashi, 400-8511, Japan

    Masashi Miyagawa

Authors
  1. Masashi Miyagawa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Masashi Miyagawa.

Appendix

Appendix

1.1 A.1 Distribution of the shortest distance

Square lattice

(13)

where

Diamond lattice

(14)

where

1.2 A.2 Distribution of the barrier distance with flexible allocation

Square lattice

(15)

where

Diamond lattice

(16)

where

1.3 A.3 Distribution of the barrier distance with fixed allocation

Square lattice

(17)

where

Diamond lattice

(18)

where

Rights and permissions

Reprints and permissions

About this article

Cite this article

Miyagawa, M. Rectilinear distance to a facility in the presence of a square barrier. Ann Oper Res 196, 443–458 (2012). https://doi.org/10.1007/s10479-012-1063-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-012-1063-z

Keywords

Search

Navigation