Skip to main content
SpringerLink
Log in

A graphical characterization of the efficient set for convex multiobjective problems

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

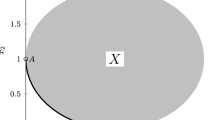
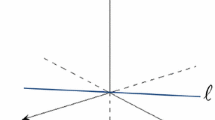
In this paper, a graphical characterization, in the decision space, of the properly efficient solutions of a convex multiobjective problem is derived. This characterization takes into account the relative position of the gradients of the objective functions and the active constraints at the given feasible solution. The unconstrained case with two objective functions and with any number of functions and the general constrained case are studied separately. In some cases, these results can provide a visualization of the efficient set, for problems with two or three variables. Besides, a proper efficiency test for general convex multiobjective problems is derived, which consists of solving a single linear optimization problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Benson, H. P. (1978). Existence of efficient solutions for vector maximization problems. Journal of Optimization Theory and Applications, 26(4), 569–580.

    Article  Google Scholar 

  • Brosowski, B., & da Silva, A. R. (1994). Simple tests for multi-criteria optimality. OR Spektrum, 16, 243–247.

    Article  Google Scholar 

  • Charnes, A., & Cooper, W. W. (1961). Management models and industrial applications for linear programming. New York: Wiley.

    Google Scholar 

  • Ecker, J. G., & Kouada, L. A. (1975). Finding efficient points for linear multiple objective programs. Mathematical Programming, 8, 375–377.

    Article  Google Scholar 

  • Lowe, T. J., Thiesse, J.-F., Ward, J. E., & Wendell, R. E. (1984). On efficient solutions to multiple objective mathematical programs. Management Science, 30(11), 1346–1349.

    Article  Google Scholar 

  • Mangasarian, O. L. (1969). Non linear programming. New York: McGraw Hill.

    Google Scholar 

  • Miettinen, K. (1999). Nonlinear multiobjective optimization. Boston: Kluwer Academic.

    Google Scholar 

  • Sawaragi, Y., Nakayama, H., & Tanino, T. (1985). Theory of multiobjective optimization. Orlando: Academic Press.

    Google Scholar 

  • Steuer, R. E. (1986). Multiple criteria optimization: theory, computation and application. New York: Wiley.

    Google Scholar 

  • Ward, J. (1989). Structure of efficient sets for convex objectives. Mathematics of Operations Research, 14(2), 249–257.

    Article  Google Scholar 

  • Wendell, R. E., & Lee, D. N. (1977). Efficiency in multiple objective optimization problems. Mathematical Programming, 12, 406–414.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Economics (Mathematics), Faculty of Economy, University of Málaga, C/Ejido, 6, Málaga, 29071, Spain

    Francisco Ruiz, Lourdes Rey & María del Mar Muñoz

Authors
  1. Francisco Ruiz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lourdes Rey
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. María del Mar Muñoz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Francisco Ruiz.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ruiz, F., Rey, L. & Muñoz, M.d.M. A graphical characterization of the efficient set for convex multiobjective problems. Ann Oper Res 164, 115–126 (2008). https://doi.org/10.1007/s10479-008-0346-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-008-0346-x

Keywords

Search

Navigation