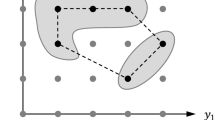
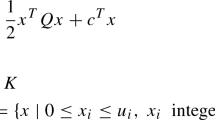Abstract
We present an algorithmic approach for solving two-stage stochastic mixed 0–1 problems. The first stage constraints of the Deterministic Equivalent Model have 0–1 variables and continuous variables. The approach uses the Twin Node Family (TNF) concept within the so-called Branch-and-Fix Coordination algorithmic framework to satisfy the nonanticipativity constraints, jointly with a Benders Decomposition scheme to solve a given LP model at each TNF integer set. As a pilot case, the structuring of a portfolio of Mortgage-Backed Securities under uncertainty in the interest rate path on a given time horizon is used. Some computational experience is reported.
Similar content being viewed by others
References
Ahmed, S. and A. Shapiro. (2002). The Sample Average Approximation Method for Stochastic Programs with Integer Recourse. Atlanta, GA, USA: School of Industrial and Systems Engineering, Georgia Institute of Technology.
Alonso-Ayuso, A., L.F. Escudero, and M.T. Ortuño. (2003). “BFC, A Branch-and-Fix Coordination Algorithmic Framework for Solving Some Types of Stochastic Pure and Mixed 0–1 Programs.” European Journal of Operational Research, 151, 503–519.
Ben-Dov, Y., L. Hayre, and V. Pica. (1992). “Mortgage Valuation Models at Prudential Securities.” Interfaces, 2, 55–71.
Benders, J.F. (1962). “Partitioning Procedures for Solving Mixed Variables Programming Problems.” Numerische Mathematik, 4, 238–252.
Birge, J.F. and F.V. Louveaux. (1997). Introduction to Stochastic Programming, Springer.
Black, F., E. Derman, and W. Toy. (1990). “A One Factor Model of Interest Rates and Its Application to Treasury Bond Options.” Financial Analysis Journal, January/February, pp. 33–39.
Carøe, C.C. and R. Schultz. (1999). “Dual Decomposition in Stochastic Integer Programming.” Operations Research Letters, 24, 37–45.
Deng, Y., J.M. Quigley, and R. Van Order. (2000). “Mortgage Terminations, Heterogeneity and the Exercise of Mortgage Options.” Econometrica 68, 275–307.
Dunn, K.B. and J.J. McConnell. (1981). “Valuation of GNMA Mortgage-Backed Securities.” The Journal of Finance 36, 599–616.
Escudero, L.F. (1995). “Robust Portfolios for Mortgage-Backed Securities.” In S.A. Zenios (Ed.), Quantitative Methods, Super Computers and AI in Finance, pp. 201–228. Stanley Thornes.
Frauendorfer, K. and M. Schürle. (1998). “Baricentric Approximation of Stochastic Interest Rate Processes.” In W.T. Ziemba and J.M. Mulvey (Eds.), Worldwide Asset and Liability Modeling, pp. 231–262. Cambridge University Press.
Hayre, L. and K. Lauterbach. (1991). “Prepayment Models and Methodologies.” In F. Fabozzi (Ed.), Handbook of Fixed-Income Securities, Chapter 37. Richard D. Irwin.
Hemmecke, R. and R. Schultz. (2001). “Decomposition Methods for Two-stage Stochastic Integer Programs.” In M. Grötschel, S.O. Krumke, and J. Rambau (Eds.), Online Optimization of Large Scale Systems, pp. 601–622 Springer.
Kang, P. and S.A. Zenios. (1992). “Complete Prepayment Models for Mortgage Backed Securities.” Managmeent Science 38, 1665–1685.
Klein Haneveld, W.K. and M.H. van der Vlerk (2001). “Optimizing Electricity Distribution using Integer Recourse Models.” In S. Uryasev and P.M. Pardalos (Eds.), Stochastic Optimization: Algorithms and Applications, pp. 137–154. Kluwer Academic Publishers.
Kleywegt, A.J., A. Shapiro, and T. Homem-de Mello. (2001). “The Sample Average Approximation Method for Stochastic Discrete Optimization.” SIAM Journal on Optimization 12, 479–502.
Longstaff, F.A. (2004). “Optimal Recursive Refinancing and the Valuation of Mortgage-Backed Securities.” NBER working paper w10422, National Bureau of Economic Research, USA, www.nber.org/papers/w10422.
Mulvey, J.M. and A.E. Thorlacius. (1998). “The Towers Perrin Global Capital Market Scenario Generation System.” In W.T. Ziemba and J.M. Mulvey (Eds.), Worldwide Asset and Liability Modeling, pp. 286–312. Cambridge University Press.
Nowak, M.P., R. Schultz, and M. Westphalen. (2002). “Optimization of Simultaneous Power Production and Trading by Stochastic Integer Programming.” Stochastic Programming E-Print Series, http://dochost.rz.hu-berlin.de/speps.
Römisch, W. and R. Schultz. (2001). “Multi-stage Stochastic Integer Programs: An Introduction.” In M. Grötschel, S.O. Krumke, and J. Rambau (Eds.), Online Optimization of Large Scale Systems, pp. 581–600. Springer.
Schultz, R. (2003). “Stochastic Programming with Integer Variables.” Mathematical Programming, Series B 97, 285–309.
Schwartz, E.S. and W.N. Torous. (1989). “Prepayment and the Valuation of Mortgage-Backed Securities.” The Journal of Finance 44, 375–392.
Stanton, R. (1995). “Rational Prepayment and the Valuation of Mortgage-Backed Securities.” The Review of Financial Studies, 8, 677–708.
Takriti, S. and J.R. Birge. (2000). “Lagrangean Solution Techniques and Bounds for Loosely Coupled Mixed-Integer Stochastic Programs.” Operations Research, 48, 91–98.
Uryasev, S. and P.M. Pardalos (Eds.). (2001). Stochastic Optimization: Algorithms and Applications, Kluwer Academic Publishers.
Wallace, S.W. and W.T. Ziemba (Eds.). (2005). Applications of Stochastic Programming, MPS-SIAM-Series in Optimization.
Zenios, S.A. (1993). “A Model for Portfolio Management with Mortgage-Backed Securities.” Annals of Operations Research, 43, 337–356.
Ziemba, W.T. and J.M. Mulvey (Eds.). (1998). Worldwide Asset and Liability Modeling. Cambridge University Press.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Escudero, L.F., Garín, A., Merino, M. et al. A two-stage stochastic integer programming approach as a mixture of Branch-and-Fix Coordination and Benders Decomposition schemes. Ann Oper Res 152, 395–420 (2007). https://doi.org/10.1007/s10479-006-0138-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-006-0138-0