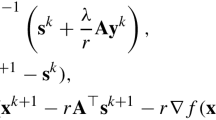Abstract
Let ℂ[−1,1] be the space of continuous functions on [−,1], and denote by Δ2 the set of convex functions f ∈ ℂ[−,1]. Also, let E n (f) and E (2) n (f) denote the degrees of best unconstrained and convex approximation of f ∈ Δ2 by algebraic polynomials of degree < n, respectively. Clearly, En (f) ≦ E (2) n (f), and Lorentz and Zeller proved that the inverse inequality E (2) n (f) ≦ cE n (f) is invalid even with the constant c = c(f) which depends on the function f ∈ Δ2.
In this paper we prove, for every α > 0 and function f ∈ Δ2, that
where c(α) is a constant depending only on α. Validity of similar results for the class of piecewise convex functions having s convexity changes inside (−1,1) is also investigated. It turns out that there are substantial differences between the cases s≦ 1 and s ≧ 2.
Similar content being viewed by others
References
Z. Ditzian and V. Totik, Moduli of Smoothness, Springer Series in Computational Mathematics, vol. 9, Springer-Verlag (New York, 1987), MR914149 (89h:41002).
V. K. Dzyadyk and I. A. Shevchuk, Theory of Uniform Approximation of Functions by Polynomials, Walter de Gruyter (Berlin, 2008).
K. A. Kopotun, Uniform estimates of monotone and convex approximation of smooth functions, J. Approx. Theory, 80 (1995), 76–107. MR1308595 (95j:41006).
K. A. Kopotun, D. Leviatan and I. A. Shevchuk, The degree of coconvex polynomial approximation, Proc. Amer. Math. Soc., 127 (1999), 409–415. MR 99c:41010.
K. A. Kopotun, D. Leviatan and I. A. Shevchuk, Convex polynomial approximation in the uniform norm: conclusion, Canad. J. Math., 57 (2005), 1224–1248. MR2178560 (2006f:41018).
K. A. Kopotun, D. Leviatan and I. A. Shevchuk, Coconvex approximation in the uniform norm: the final frontier, Acta Math. Hungar., 110 (2006), 117–151. MR2198418 (2006i:41014).
D. Leviatan and I. A. Shevchuk, Coconvex approximation, J. Approx. Theory, 118 (2002), 20–65. MR 2003f:41027.
G. G. Lorentz and K. L. Zeller, Degree of approximation by monotone polynomials. II, J. Approx. Theory, 2 (1969), 265–269. MR0244677 (39 #5991).
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Jóska Szabados on his 70th birthday
The first author was supported by NSERC of Canada, the third author by Grant “Dnipro”.
Rights and permissions
About this article
Cite this article
Kopotun, K., Leviatan, D. & Shevchuk, I.A. Are the degrees of best (co)convex and unconstrained polynomial approximation the same?. Acta Math Hung 123, 273–290 (2009). https://doi.org/10.1007/s10474-009-8111-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10474-009-8111-4