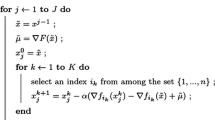Skip to main content
SpringerLink
Log in

Hybrid regularized cone-beam reconstruction for axially symmetric object tomography

  • Published:
Acta Mathematica Scientia Aims and scope Submit manuscript

Abstract

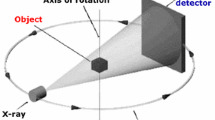
In this paper, we consider 3D tomographic reconstruction for axially symmetric objects from a single radiograph formed by cone-beam X-rays. All contemporary density reconstruction methods in high-energy X-ray radiography are based on the assumption that the cone beam can be treated as fan beams located at parallel planes perpendicular to the symmetric axis, so that the density of the whole object can be recovered layer by layer. Considering the relationship between different layers, we undertake the cone-beam global reconstruction to solve the ambiguity effect at the material interfaces of the reconstruction results. In view of the anisotropy of classical discrete total variations, a new discretization of total variation which yields sharp edges and has better isotropy is introduced in our reconstruction model. Furthermore, considering that the object density consists of continually changing parts and jumps, a high-order regularization term is introduced. The final hybrid regularization model is solved using the alternating proximal gradient method, which was recently applied in image processing. Density reconstruction results are presented for simulated radiographs, which shows that the proposed method has led to an improvement in terms of the preservation of edge location.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Radon J, Über die bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten. Berichte Sächsische Akademie der Wissenschaften, Leipzig, Mathematische-Physikalische Klass, 1917, 69: 262–267

    MATH  Google Scholar 

  2. Wei S, Wang S, Xu H, Regularization method for axially symmetric objects tomography from a single X-ray projection data. Journal of Image and Graphics, 2008, 13: 2275–2280

    Google Scholar 

  3. Chan R H, Liang H, Wei S, et al, High-order total variation regularization approach for axially symmetric object tomography from a single radiograph. Inverse Problems and Imaging, 2015, 9: 55–77

    Article  MathSciNet  MATH  Google Scholar 

  4. Lewitt R M, Reconstruction algorithms: Transform methods. Proceedings of the IEEE, 1983, 71: 390–408

    Article  Google Scholar 

  5. Natterer F. The Mathematics of Computerized Tomography. New York: Wiley, 1986

    Book  MATH  Google Scholar 

  6. Kak A C, Slaney M. Principles of Computerized Tomographic Imaging. New York: IEEE Press, 1987

    MATH  Google Scholar 

  7. Feldkamp L A, Davis L C, Kress J W, Practical cone-beam algorithm. Journal of the Optical Society of America A, 1984, 1: 612–619

    Article  Google Scholar 

  8. Wang G, Lin T H, Cheng P C, et al, A general cone-beam reconstruction algorithm. IEEE Transactions on Medical Imaging, 1993, 12: 486–496

    Article  Google Scholar 

  9. Gordon R, Bender R, Herman G T, Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. Journal of Theoretical Biology, 1970, 29: 471–481

    Article  Google Scholar 

  10. Gilbert P, Iterative methods for the three-dimensional reconstruction of an object from projections. Journal of Theoretical Biology, 1972, 36: 105–117

    Article  Google Scholar 

  11. Andersen A H, Kak A C, Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm. Ultrasonic Imaging, 1984, 6: 81–94

    Article  Google Scholar 

  12. Luo S, Meng R, Wei S, et al. Data-driven Method for 3D Axis-symmetric object reconstruction from single cone-beam projection data//Yuan J, Lu H. Proceedings of the Third International Symposium on Image Computing and Digital Medicine. New York: ACM, 2019: 288–292

    Chapter  Google Scholar 

  13. Rudin L I, Osher S, Fatemi E, Nonlinear total variation based noise removal algorithms. Physica D, 1992, 60: 259–268

    Article  MathSciNet  MATH  Google Scholar 

  14. Sauer K, Bouman C, Bayesian estimation of transmission tomograms using segmentation based optimization. IEEE Transactions on Nuclear Science, 1992, 39: 1144–1152

    Article  Google Scholar 

  15. Chambolle A, Caselles V, Novaga M, et al. An introduction to total variation for image analysis//Fornasier M. Theoretical Foundations and Numerical Methods for Sparse Recovery. Berlin: Walter de Gruyter, 2010: 263–340

    MATH  Google Scholar 

  16. Chambolle A, Pock T, A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision, 2011, 40: 120–145

    Article  MathSciNet  MATH  Google Scholar 

  17. Burger M, Osher S. A guide to the TV zoo//Burger M, Osher S. Level Set and PDE Based Reconstruction Methods in Imaging. Switzerland: Springer International Publishing, 2013: 1–70

    Chapter  Google Scholar 

  18. Chambolle A. Total variation minimization and a class of binary MRF models//Rangarajan A, Vemuri B, Yuille A L. Energy Minimization Methods in Computer Vision and Pattern Recognition. Berlin: Springer-Verlag, 2005: 136–152

    Chapter  Google Scholar 

  19. Abergel R, Louchet C, Moisan L, et al. Total variation restoration of images corrupted by Poisson noise with iterated conditional expectations//Aujol J-F, Nikolova M, Papadakis N. International Conference on Scale Space and Variational Methods in Computer Vision. Switzerland: Springer International Publishing, 2015: 178–190

    Google Scholar 

  20. Chambolle A, Levine S E, Lucier B J, An upwind finite-difference method for total variation-based image smoothing. SIAM Journal on Imaging Sciences, 2011, 4: 277–299

    Article  MathSciNet  MATH  Google Scholar 

  21. Condat L, Discrete total variation: new Definition and minimization. SIAM Journal on Imaging Sciences, 2016, 10: 1258–1290

    Article  MathSciNet  MATH  Google Scholar 

  22. Abergel R, Moisan L, The Shannon total variation. Journal of Mathematical Imaging and Vision, 2016, 59: 1–30

    MathSciNet  MATH  Google Scholar 

  23. Hosseini A. A regularization term based on a discrete total variation for mathematical image processing. 2017. http://arxiv.org/pdf/1711.10534.pdf

  24. Li F, Shen C, Fan J, et al, Image restoration combining a total variational filter and a fourth-order filter. Journal of Visual Communication and Image Representation, 2007, 18: 322–330

    Article  Google Scholar 

  25. Lysaker M, Tai X C, Iterative image restoration combining total variation minimization and a second-order functional. International Journal of Computer Vision, 2006, 66: 5–18

    Article  MATH  Google Scholar 

  26. Papafitsoros K, Schönlieb C B, A combined first and second order variational approach for image reconstruction. Journal of Mathematical Imaging and Vision, 2014, 48: 308–338

    Article  MathSciNet  MATH  Google Scholar 

  27. Thanh D N H, Prasath V B S, Hieu L M, et al, An adaptive method for image restoration based on high-order total variation and inverse gradient. Signal, Image and Video Processing, 2020, 14: 1189–1197

    Article  Google Scholar 

  28. Chan T, Marquina A, Mulet P, High-order total variation-based image restoration. SIAM Journal on Scientific Computing, 2000, 22: 503–516

    Article  MathSciNet  MATH  Google Scholar 

  29. Chen H Z, Song J P, Tai X C, A dual algorithm for minimization of the LLT model. Advances in Computational Mathematics, 2009, 31: 115–130

    Article  MathSciNet  MATH  Google Scholar 

  30. You Y L, Kaveh M, Fourth-order partial differential equation for noise removal. IEEE Transactions on Image Processing, 2000, 9: 1723–1730

    Article  MathSciNet  MATH  Google Scholar 

  31. Lysaker M, Lundervold A, Tai X C, Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time. IEEE Transactions on Image Processing, 2003, 12: 1579–1590

    Article  MATH  Google Scholar 

  32. Steidl G, A note on the dual treatment of higher order regularization functionals. Computing, 2005, 76: 135–148

    Article  MathSciNet  MATH  Google Scholar 

  33. Benning M, Higher-order TV methods-Enhancement via Bregman iteration. Journal of Scientific Computing, 2013, 54: 269–310

    Article  MathSciNet  MATH  Google Scholar 

  34. Lefkimmiatis S, Bourquard A, Unser M, Hessian-based norm regularization for image restoration with biomedical applications. IEEE Transactions on Image Processing, 2012, 21: 983–995

    Article  MathSciNet  MATH  Google Scholar 

  35. Bauschke H H, Combettes P L. Convex Analysis and Monotone Operator Theory in Hilbert Space. New York: Springer, 2011

    Book  MATH  Google Scholar 

  36. Asaki T J, Chartrand R, Vixie K R, et al, Abel inversion using total-variation regularization. Inverse Problems, 2005, 21: 1895–1903

    Article  MathSciNet  MATH  Google Scholar 

  37. Asaki T J, Campbell P R, Chartrand R, et al, Abel inversion using total variation regularization: applications. Inverse Problems in Science and Engineering, 2006, 14: 873–885

    Article  MathSciNet  MATH  Google Scholar 

  38. Abraham R, Bergounioux M, Trélat E, A penalization approach for tomographic reconstruction of binary axially symmetric objects. Applied Mathematics and Optimization, 2008, 58: 345–371

    Article  MathSciNet  MATH  Google Scholar 

  39. Chen K, Wei S, On some variational models and their algorithms for axially symmetric objects tomography from a single X-ray source. Scientia Sinica, 2015, 45: 1537–1548

    Google Scholar 

  40. Ma S, Alternating proximal gradient method for convex minimization. Journal of Scientific Computing, 2016, 68: 1–27

    Article  MathSciNet  MATH  Google Scholar 

  41. He B, Yang H, Wang S, Alternating direction method with self-adaptive penalty parameters for monotone variational inequalities. Journal of Optimization Theory and Applications, 2000, 106: 337–356

    Article  MathSciNet  MATH  Google Scholar 

  42. Donoho L D, De-noising by soft-thresholding. IEEE Transactions on Information Theory, 1995, 41: 613–627

    Article  MathSciNet  MATH  Google Scholar 

  43. Boyd S, Parikh N, Chu E, et al, Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2011, 3: 1–122

    Article  MATH  Google Scholar 

  44. Canny J, A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8: 679–698

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Applied Physics and Computational Mathematics, Beijing, 100094, China

    Xinge Li, Suhua Wei & Haibo Xu

  2. LSEC, ICMSEC, Academy of Mathematics and Systems Science, CAS, Beijing, 100190, China

    Chong Chen

Authors
  1. Xinge Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Suhua Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Haibo Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chong Chen.

Additional information

X. Li was supported by National Postdoctoral Program for Innovative Talents (BX201700038). S. Wei was supported by NSFC (11571003). H. Xu was supported by NSFC (11675021). C. Chen was supported by Beijing Natural Science Foundation (Z180002).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, X., Wei, S., Xu, H. et al. Hybrid regularized cone-beam reconstruction for axially symmetric object tomography. Acta Math Sci 42, 403–419 (2022). https://doi.org/10.1007/s10473-022-0122-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10473-022-0122-z

Key words

2010 MR Subject Classification

Search

Navigation