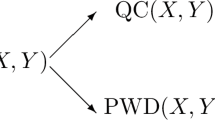
Calvert calculated the complexity of the computable isomorphism problem for a number of familiar classes of structures. Rosendal suggested that it might be interesting to do the same for the computable embedding problem. By the computable isomorphism problem and (computable embedding problem) we mean the difficulty of determining whether there exists an isomorphism (embedding) between two members of a class of computable structures. For some classes, such as the class of \( \mathbb{Q} \)-vector spaces and the class of linear orderings, it turns out that the two problems have the same complexity. Moreover, calculations are essentially the same. For other classes, there are differences. We present examples in which the embedding problem is trivial (within the class) and the computable isomorphism problem is more complicated. We also give an example in which the embedding problem is more complicated than the isomorphism problem.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. S. Goncharov and J. F. Knight, “Computable structure and non-structure theorems,” Algebra Logika, 41, No. 6, 639–681 (2002).
C. J. Ash and J. F. Knight, Computable Structures and the Hyperarithmetical Hierarchy, Elsevier, Amsterdam (2000).
H. Rogers, Theory of Recursive Functions and Effective Computability, McGraw-Hill, New York (1967).
W. Calvert, “Algebraic structure and computable structure,” Ph. D. Thesis, Notre Dame Univ. (2005).
W. Calvert, “The isomorphism problem for classes of computable fields,” Arch. Math. Log., 75, No. 3, 327–336 (2004).
W. Calvert, “The isomorphism problem for computable Abelian p-groups of bounded length,” J. Symb. Log., 70, No. 1, 331–345 (2005).
J. F. Knight, S. Miller, and M. Vanden Boom, “Turing computable embeddings,” J. Symb. Log., 72, No. 3, 901–918 (2007).
R. Downey and A. Montalbán, “The isomorphism problem for torsion-free Abelian groups is analytic complete,” J. Alg., 320, No. 6, 2291–2300 (2008).
V. Harizanov, S. Lempp, C. F. McCoy, A. S. Morozov, and D. Reed Solomon, “On the isomorphism problem for nilpotent rings, distributive lattices, nilpotent groups, and nilpotent semigroups,” Preprint.
D. Marker, Model Theory: An Introduction, Grad. Texts Math., 217, Springer, New York (2002).
W. Calvert, D. Cummins, J. F. Knight, and S. Miller, “Comparing classes of finite structures,” Algebra Logika, 43, No. 6, 666–701 (2004).
H. Friedman and L. Stanley, “A Borel reducibility theory for classes of computable structures,” J. Symb. Log., 54, No. 3, 894–914 (1989).
A. I. Mal’tsev, “On a correspondence between rings and groups,” Mat. Sb., 50, No. 3, 257–266 (1960).
D. R. Hirschfeldt, B. Khoussainov, R. A. Shore, and A. M. Slinko, “Degree spectra and computable dimension in algebraic structures,” Ann. Pure Appl. Log., 115, Nos. 1–3, 71–113 (2002).
R. C. Lyndon and P. E. Schupp, Combinatorial Group Theory, Springer, Berlin (1977).
G. Higman, B. H. Neumann, and H. Neumann, “Embedding theorems for groups,” J. London Math. Soc., 24, 247–254 (1950).
G. S. Sacerdote, “Elementary properties of free groups,” Trans. Am. Math. Soc., 178, 127–138 (1973).
W. Calvert, D. Cenzer, V. Harizanov, and A. Morozov, “Effective categoricity of equivalence structures,” Ann. Pure Appl. Log., 141, Nos. 1/2, 61–78 (2006).
C. J. Ash and J. F. Knight, “Pairs of recursive structures,” Ann. Pure Appl. Log., 46, No. 3, 211–234 (1990).
A. T. Nurtazin, “Computable classes and algebraic criteria for autostability,” Ph. D. Thesis, Institute of Mathematics and Mechanics, Alma-Ata (1974).
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by NSF, binational grant DMS-0554841.
Supported by NSF, grants DMS-0139626 and DMS-0353748.
Supported by NSF, grant DMS-0704265.
Supported by the Grants Council (under RF President) for Undergraduate and Postgraduate Studies Abroad.
Translated from Algebra i Logika, Vol. 50, No. 6, pp. 707-732, November-December, 2011.
Rights and permissions
About this article
Cite this article
Carson, J., Fokina, E., Harizanov, V.S. et al. The computable embedding problem. Algebra Logic 50, 478–493 (2012). https://doi.org/10.1007/s10469-012-9160-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10469-012-9160-2