Independence test and canonical correlation analysis based on the alignment between kernel matrices for multivariate functional data

Abstract

In the case of vector data, Gretton et al. (Algorithmic learning theory. Springer, Berlin, pp 63–77, 2005) defined Hilbert–Schmidt independence criterion, and next Cortes et al. (J Mach Learn Res 13:795–828, 2012) introduced concept of the centered kernel target alignment (KTA). In this paper we generalize these measures of dependence to the case of multivariate functional data. In addition, based on these measures between two kernel matrices (we use the Gaussian kernel), we constructed independence test and nonlinear canonical variables for multivariate functional data. We show that it is enough to work only on the coefficients of a series expansion of the underlying processes. In order to provide a comprehensive comparison, we conducted a set of experiments, testing effectiveness on two real examples and artificial data. Our experiments show that using functional variants of the proposed measures, we obtain much better results in recognizing nonlinear dependence.

1 Introduction

The theory and practice of statistical methods in situations where the available data are functions (instead of real numbers or vectors) is often referred to as Functional Data Analysis (FDA). The term Functional Data Analysis was already used by Ramsay and Dalzell (1991) two decades ago. This subject has become increasingly popular from the end of the 1990s and is now a major research field in statistics (Cuevas 2014). Good access to the large literature in this field comes from the books by Ramsay and Silverman (2002, 2005), Ferraty and Vieu (2006), and Horváth and Kokoszka (2012). Special issues devoted to FDA topics have been published by different journals, including Statistica Sinica 14(3) (2004), Computational Statistics 22(3) (2007), Computational Statistics and Data Analysis 51(10) (2007), Journal of Multivariate Analysis 101(2) (2010), Advances in Data Analysis and Classification 8(3) (2014).

The range of real world applications, where the objects can be thought of as functions, is as diverse as speech recognition, spectrometry, meteorology, medicine or clients segmentation, to cite just a few (Ferraty and Vieu 2003; James et al. 2009; Martin-Baragan et al. 2014; Devijver 2017).

The uncentered kernel alignment originally was introduced by Cristianini et al. (2001). Gretton et al. (2005) defined Hilbert–Schmidt Independence Criterion (HSIC) and the empirical HSIC. Centered kernel target alignment (KTA) was introduced by Cortes et al. (2012). This measure is a normalized version of HSIC. Zhang et al. (2011) gave an interesting kernel-based independence test. This independence testing method is closely related to the one based on the Hilbert–Schmidt independence criterion (HSIC) proposed by Gretton et al. (2008). Gretton et al. (2005) described a permutation-based kernel independence test. There is a lot of work in the literature for kernel alignment and its applications (good overview can be found in Wang et al. 2015).

This work is devoted to a generalization of these measures of dependence to the case of multivariate functional data. In addition, based on these measures we constructed independence test and nonlinear canonical correlation variables for multivariate functional data. These results are based on the assumption that the applied kernel function is Gaussian. Functional HSIC and KTA canonical correlation analysis can be viewed as natural nonlinear extension of functional canonical correlation analysis (FCCA). So, we propose two nonlinear functional CCA extensions that capture nonlinear relationship. Moreover, both algorithms are capable of extracting also linear dependency. Additionally, we show that functional KTA approach is only a normalized variant of HSIC coefficient also for functional data. Finally, we propose some interpretation of module weighting functions for functional canonical correlations.

Section 2 provides an overview of centered measures alignment for random vectors. They are defined by such concepts as: kernel function alignment, kernel matrix alignment, and Hilbert–Schmidt Independence Criterion (HSIC) and associations between them have been shown. Functional data can be seen as values of random processes. In our paper, the multivariate random function $\pmb X$ and $\pmb Y$ have special representation (8) in finite dimensional subspaces of the spaces of square integrable functions on the given intervals. In Sect. 3 we present kernel-based independence test. Section 4 discusses the concept of alignment for multivariate functional data. The kernel function, the alignment between two kernels functions, the centered kernel alignment (KTA) between two kernel matrices and the empirical Hilbert–Schmidt Independence Criterion (HSIC) are defined. The HSIC was used as the basis for an independence test. In Sect. 5 we present kernel-based independence test for multivariate functional data. In Sect. 5, based on the concept of alignment between kernel matrices, nonlinear canonical variables were constructed. It is a generalization of the results of Chang et al. (2013) for random vectors. In Sect. 5 we present an one artificial and two real examples which confirm the usefulness of proposed coefficients in detection of nonlinear dependency for group of variables.

2 An overview of kernel alignment and its applications

We introduce the following notational convention. Throughout this section, $\pmb {X}$ and $\pmb {Y}$ are random vectors, with domains $\mathbb {R}^p$ and $\mathbb {R}^q$, respectively. Let $P_{\pmb {X},\pmb {Y}}$ be a joint probability measure on ($\mathbb {R}^p\times \mathbb {R}^q$, $\Gamma \times \Lambda$) (here $\Gamma$ and $\Lambda$ are the Borel $\sigma$-algebras on $\mathbb {R}^p$ and $\mathbb {R}^q$, respectively), with associated marginal probability measures $P_{\pmb {X}}$ and $P_{\pmb {Y}}$.

Definition 1

(Kernel functions, Shawe-Taylor and Cristianini 2004) A kernel is a function k that for all $\pmb x, \pmb x'\in \mathbb {R}^p$ satisfies

$$\begin{aligned} k(\pmb x, \pmb x') = \langle \pmb \varphi (\pmb x), \pmb \varphi (\pmb x')\rangle _\mathcal {H}, \end{aligned}$$

where $\varphi$ is a mapping from $\mathbb {R}^p$ to an inner product feature space $\mathcal {H}$

$$\begin{aligned} \varphi :\pmb x\rightarrow \varphi (\pmb x)\in \mathcal {H}. \end{aligned}$$

We call $\pmb \varphi$ a feature map.

A kernel function can be interpreted as a kind of similarity measure between the vectors $\pmb x$ and $\pmb x'$.

Definition 2

(Gram matrix, Mercer 1909; Riesz 1909; Aronszajn 1950) Given a kernel k and inputs $\pmb x_1,\ldots , \pmb x_n\in \mathbb {R}^p$, the $n\times n$ matrix $\pmb K$ with entries $K_{ij}=k(\pmb x_i, \pmb x_j)$ is called the Gram matrix (kernel matrix) of k with respect to $\pmb x_1,\ldots , \pmb x_n$.

Definition 3

(Positive semi-definite matrix, Hofmann et al. 2008) A real $n\times n$ symmetric matrix $\pmb K$ with entries $K_{ij}$ satisfying

$$\begin{aligned} \sum _{i=1}^n\sum _{j=1}^nc_ic_jK_{ij}\ge 0 \end{aligned}$$

for all $c_i\in \mathbb {R}$ is called positive semi-definite.

Definition 4

(Positive semi-definite kernel, Mercer 1909; Hofmann et al. 2008) A function $k:\mathbb {R}^p\times \mathbb {R}^p\rightarrow \mathbb {R}$ which for all $n\in \mathbb {N},\ \pmb x_i\in \mathbb {R}^p,\ i=1,\ldots ,n$ gives rise to a positive semi-definite Gram matrix is called a positive semi-definite kernel.

This raises an interesting question: given a function of two variables $k(\pmb x, \pmb x')$, does there exist a function $\pmb \varphi (\pmb x)$ such that $k(\pmb x, \pmb x') = \langle \pmb \varphi (\pmb x), \pmb \varphi (\pmb x')\rangle _\mathcal {H}?$ The answer is provided by Mercer’s theorem (1909) which says, roughly, that if k is positive semi-definite then such a $\varphi$ exists.

Often, we will not known $\pmb {\phi }$, but a kernel function $k:\mathbb {R}^p\times \mathbb {R}^p\rightarrow \mathbb {R}$ that encodes the inner product in $\mathcal {H}$, instead.

Popular positive semi-definite kernel functions on $\mathbb {R}^p$ include the polynomial kernel of degree $d>0$, $k(\pmb {x},\pmb {x}')= (1 + \pmb x^\top \pmb x')^d$, the Gaussian kernel $k(\pmb {x},\pmb {x}')=\exp (-\lambda \Vert \pmb {x}-\pmb {x}'\Vert ^2)$, $\lambda >0$, and the Laplace kernel $k(\pmb {x},\pmb {x}')=\exp (-\lambda \Vert \pmb {x}-\pmb {x}'\Vert )$, $\lambda >0$. In this paper we use, the Gaussian kernel.

We start with the definition of centering and the analysis of its relevant properties.

2.1 Centered kernel functions

A feature mapping $\pmb {\phi }:\mathbb {R}^p \rightarrow \mathcal {H}$ is centered by subtracting from it its expectation, that is transforming $\pmb {\phi }(\pmb {x})$ to $\tilde{\pmb {\phi }}(\pmb {x})=\pmb {\phi }(\pmb {x})-{{\mathrm{E}}}_{\pmb {X}}[\pmb {\phi }(\pmb {X})]$, where ${{\mathrm{E}}}_{\pmb {X}}$ denotes the expected value of $\pmb {\phi }(\pmb {X})$ when $\pmb {X}$ is distributed according to $P_{\pmb {X}}$. Centering a positive semi-definite kernel function $k:\mathbb {R}^p\times \mathbb {R}^p\rightarrow \mathbb {R}$ consists centering in the feature mapping $\pmb {\phi }$ associated to k. Thus, the the centered kernel $\tilde{k}$ associated to k is defined by

$$\begin{aligned} \tilde{k}(\pmb {x},\pmb {x}')&= \langle \pmb {\phi }(\pmb {x})-{{\mathrm{E}}}_{\pmb {X}}[\pmb {\phi }(\pmb {X})], \pmb {\phi }(\pmb {x}')-{{\mathrm{E}}}_{\pmb {X}'}[\pmb {\phi }(\pmb {X}')]\rangle \\&=k(\pmb {x},\pmb {x}')-{{\mathrm{E}}}_{\pmb {X}}[k(\pmb {X},\pmb {x}')]-{{\mathrm{E}}}_{\pmb {X}'}[k(\pmb {x},\pmb {X}')]+{{\mathrm{E}}}_{\pmb {X},\pmb {X}'}[k(\pmb {X},\pmb {X}')], \end{aligned}$$

assuming the expectations exist. Here, the expectation is taken over independent copies $\pmb {X}$, $\pmb {X}'$ distributed according to $P_{\pmb {X}}$. We see that, $\tilde{k}$ is also a positive semi-definite kernel. Note also that for a centered kernel $\tilde{k}$, ${{\mathrm{E}}}_{\pmb {X},\pmb {X}'}[\tilde{k}(\pmb {X},\pmb {X}')]=0$, that is, centering the feature mapping implies centering the kernel function.

2.2 Centered kernel matrices

Let $\{\pmb {x}_1,\ldots ,\pmb {x}_n\}$ be a finite subset of $\mathbb {R}^p$. A feature mapping $\pmb {\phi }(\pmb {x}_i)$, $i=1,\ldots ,n$, is centered by subtracting from it its empirical expectation, i.e., leading to $\bar{\pmb {\phi }}(\pmb {x}_i)=\pmb {\phi }(\pmb {x}_i)-\overline{\pmb {\phi }}$, where $\overline{\pmb {\phi }}=\frac{1}{n}\sum _{i=1}^n\pmb {\phi }(\pmb {x}_i)$. The kernel matrix $\pmb {K} = (K_{ij})$ associated to the kernel function k and the set $\{\pmb {x}_1,\ldots ,\pmb {x}_n\}$ is centered by replacing it with $\widetilde{\pmb {K}} = (\widetilde{K}_{ij})$ defined for all $i,j=1,2,\ldots ,n$ by

$$\begin{aligned} \tilde{K}_{ij}=K_{ij}-\frac{1}{n} \sum _{i=1}^nK_{ij}-\frac{1}{n}\sum _{j=1}^nK_{ij}+\frac{1}{n^2}\sum _{i,j=1}^nK_{ij}, \end{aligned}$$

(1)

where $K_{ij}=k(\pmb {x}_i,\pmb {x}_j)$, $i,j=1,\ldots ,n$.

The centered kernel matrix $\widetilde{\pmb {K}}$ is a positive semi-definite matrix. Also, as with the kernel function $\frac{1}{n^2}\sum _{i,j}^n\tilde{K}_{ij}=0$.

Let $\langle \cdot ,\cdot \rangle _F$ denote the Frobenius product and $\Vert \cdot \Vert _F$ the Frobenius norm defined for all $\pmb {A},\pmb {B}\in \mathbb {R}^{n\times n}$ by

$$\begin{aligned} \langle \pmb {A},\pmb {B}\rangle _F&={{\mathrm{tr}}}(\pmb {A}^\top \pmb {B}),\\ \Vert \pmb {A}\Vert _F&=(\langle \pmb {A},\pmb {A}\rangle _F)^{1/2}. \end{aligned}$$

Then, for any kernel matrix $\pmb {K}\in \mathbb {R}^{n\times n}$, the centered kernel matrix $\widetilde{\pmb {K}}$ can be expressed as follows (Schölkopf et al. 1998):

$$\begin{aligned} \widetilde{\pmb {K}}=\pmb {H}\pmb {K}\pmb {H}, \end{aligned}$$

(2)

where $\pmb {H}=\pmb {I}_n-\frac{1}{n}\pmb {1}_n\pmb {1}_n^\top$, $\pmb {1}_n\in \mathbb {R}^{n\times 1}$ denote the vector with all entries equal to one, and $\pmb {I}_n$ the identity matrix of order n. The matrix $\pmb H$ is called “centering matrix”.

Since $\pmb {H}$ is the idempotent matrix ($\pmb {H}^2=\pmb {H}$), then we get for any two kernel matrices $\pmb {K}$ and $\pmb {L}$ based on the subset $\{\pmb {x}_1,\ldots ,\pmb {x}_n\}$ of $\mathbb {R}^p$ and the subset $\{\pmb {y}_1,\ldots ,\pmb {y}_n\}$ of $\mathbb {R}^q$, respectively,

$$\begin{aligned} \langle \widetilde{\pmb {K}},\widetilde{\pmb {L}}\rangle _F=\langle \pmb {K},\widetilde{\pmb {L}}\rangle _F=\langle \widetilde{\pmb {K}},\pmb {L}\rangle _F. \end{aligned}$$

(3)

2.3 Centered kernel alignment

Definition 5

(Kernel function alignment, Cristianini et al. 2001; Cortes et al. 2012) Let k and l be two kernel functions defined over $\mathbb {R}^p\times \mathbb {R}^p$ and $\mathbb {R}^q\times \mathbb {R}^q$, respectively, such that $0<{{\mathrm{E}}}_{\pmb {X},\pmb {X}'}[\tilde{k}^2(\pmb {X},\pmb {X}')]<\infty$ and $0<{{\mathrm{E}}}_{\pmb {Y},\pmb {Y}'}[\tilde{l}^{2}(\pmb {Y},\pmb {Y}')]<\infty$, where $\pmb {X},\pmb {X}'$ and $\pmb {Y},\pmb {Y}'$ are independent copies distributed according to $P_{\pmb {X}}$ and $P_{\pmb {Y}}$, respectively. Then the alignment between k and l is defined by

$$\begin{aligned} \rho (k, l)=\frac{{{\mathrm{E}}}_{\pmb {X}, \pmb {X'}, \pmb {Y}, \pmb {Y'}}[\tilde{k}(\pmb {X},\pmb {X}')\tilde{l}(\pmb {Y},\pmb {Y}')]}{\sqrt{{{\mathrm{E}}}_{\pmb {X}, \pmb {X}'}[\tilde{k}^2(\pmb {X},\pmb {X}')]{{\mathrm{E}}}_{\pmb {Y}, \pmb {Y'}}[\tilde{l}^2(\pmb {Y},\pmb {Y}')]}}. \end{aligned}$$

We can define similarly the alignment between two kernel matrices $\pmb {K}$ and $\pmb {L}$ based on the finite subset $\{\pmb {x}_1,\ldots ,\pmb {x}_n\}$ and $\{\pmb {y}_1,\ldots ,\pmb {y}_n\}$, respectively.

Definition 6

(Kernel matrix alignment, Cortes et al. 2012) Let $\pmb {K}\in \mathbb {R}^{n\times n}$ and $\pmb {L}\in \mathbb {R}^{n\times n}$ be two kernel matrices such that $\Vert \widetilde{\pmb {K}} \Vert _F\ne 0$ and $\Vert \widetilde{\pmb {L}}\Vert _F\ne 0$. Then, the centered kernel target alignment (KTA) between $\pmb {K}$ and $\pmb {L}$ is defined by

$$\begin{aligned} \hat{\rho }(\pmb {K},\pmb {L})=\frac{\langle \widetilde{\pmb {K}},\widetilde{\pmb {L}}\rangle _F}{\Vert \widetilde{\pmb {K}} \Vert _F \Vert \widetilde{\pmb {L}} \Vert _F}. \end{aligned}$$

(4)

Here, by the Cauchy–Schwarz inequality, $\hat{\rho }(\pmb {K},\pmb {L})\in [-1,1]$ and in fact $\hat{\rho }(\pmb {K},\pmb {L})\in [0,1]$ when $\pmb {K}$ and $\pmb {L}$ are the kernel matrices of the positive semi-definite kernel $\tilde{k}$ and $\tilde{l}$.

Gretton et al. (2005) defined Hilbert–Schmidt Independence Criterion (HSIC) as a test statistic to distinguish between null hypothesis $H_0:P_{\pmb X, \pmb Y}=P_{\pmb X}P_{\pmb Y}$ (equivalently we may write $\pmb X{\perp \!\!\!\perp }\pmb Y$) and alternative hypothesis $H_1:P_{\pmb X, \pmb Y} \ne P_{\pmb X}P_{\pmb Y}$.

Definition 7

(Reproducing kernel Hilbert space, Riesz 1909; Mercer 1909; Aronszajn 1950) Consider a Hilbert space $\mathcal {H}$ of functions from $\mathbb {R}^p$ to $\mathbb {R}$. Then $\mathcal {H}$ is a reproducing kernel Hilbert space (RKHS) if for each $\pmb {x}\in \mathbb {R}^p$, the Dirac evaluation operator $\delta _{\pmb {x}}:\mathcal {H}\rightarrow \mathbb {R}$, which maps $f\in \mathcal {H}$ to $f(\pmb {x})\in \mathbb {R}$, is a bounded linear functional.

Let $\varphi :\mathbb {R}^p\rightarrow \mathcal {H}$ be a map such that for all $\pmb x, \pmb x'\in \mathbb {R}^p$ we have $\langle \pmb {\phi }(\pmb {x}),\pmb {\phi }(\pmb {x}')\rangle _{\mathcal {H}}=k(\pmb {x},\pmb {x}')$, where $k:\mathbb {R}^p\times \mathbb {R}^p\rightarrow \mathbb {R}$ is a unique positive semi-definite kernel. We will require in particular that $\mathcal {H}$ be separable (it must have a complete, countable orthonormal system). We likewise define a second separable RKHS $\mathcal {G}$, with kernel $l(\cdot , \cdot )$ and feature map $\pmb {\psi }$, on the separable space $\mathbb {R}^q$.

We may now define the mean elements $\mu _{\pmb X}$ and $\mu _{\pmb Y}$ with respect to the measures $P_{\pmb {X}}$ and $P_{\pmb {Y}}$ as those members of $\mathcal {H}$ and $\mathcal {G}$, respectively, for which

$$\begin{aligned} \langle \mu _{\pmb {X}},f\rangle _{\mathcal {H}}&={{\mathrm{E}}}_{\pmb {X}}[\langle \pmb {\phi }(\pmb {X}),f\rangle _{\mathcal {H}}]={{\mathrm{E}}}_{\pmb {X}}[f(\pmb {X})],\\ \langle \mu _{\pmb {Y}},g\rangle _{\mathcal {G}}&={{\mathrm{E}}}_{\pmb {Y}}[\langle \pmb {\psi }(\pmb {Y}),g\rangle _{\mathcal {G}}]={{\mathrm{E}}}_{\pmb {Y}}[g(\pmb {Y})], \end{aligned}$$

for all functions $f\in \mathcal {H}$, $g\in \mathcal {G}$, where $\pmb {\phi }$ is the feature map from $\mathbb {R}^p$ to the RKHS $\mathcal {H}$, and $\pmb {\psi }$ maps from $\mathbb {R}^q$ to $\mathcal {G}$ and assuming the expectations exist.

Finally, $\Vert \mu _{\pmb {X}}\Vert _{\mathcal {H}}^2$ can be computed by applying the expectation twice via

$$\begin{aligned} \Vert \mu _{\pmb {X}}\Vert _{\mathcal {H}}^2={{\mathrm{E}}}_{\pmb {X},\pmb {X}'}[\langle \pmb {\phi }(\pmb {X}),\pmb {\phi }(\pmb {X}')\rangle _{\mathcal {H}}] ={{\mathrm{E}}}_{\pmb {X},\pmb {X}'}[k(\pmb {X},\pmb {X}')], \end{aligned}$$

assuming the expectations exist. The expectation is taken over independent copies $\pmb {X},\pmb {X}'$ distributed according to $P_{\pmb {X}}$. The means $\mu _{\pmb {X}}$, $\mu _{\pmb {Y}}$ exist when positive semi-definite kernels k and l are bounded. We are now in a position to define the cross-covariance operator.

Definition 8

(Cross-covariance operator, Gretton et al. 2005) The cross-covariance operator $\pmb C_{\pmb X, \pmb Y}:\mathcal {G}\rightarrow \mathcal {H}$ associated with the joint probability measure $P_{\pmb {X},\pmb {Y}}$ on ($\mathbb {R}^p\times \mathbb {R}^q$, $\Gamma \times \Lambda$) is a linear operator $\pmb C_{\pmb X, \pmb Y}:\mathcal {G}\rightarrow \mathcal {H}$ defined as

$$\begin{aligned} \pmb {C}_{\pmb {X},\pmb {Y}}={{\mathrm{E}}}_{\pmb {X},\pmb {Y}}[\phi (\pmb {X})\otimes \psi (\pmb {Y})]-\mu _{\pmb {X}}\otimes \mu _{\pmb {Y}}, \end{aligned}$$

for all $f\in \mathcal {H}$ and $g\in \mathcal {G}$, where the tensor product operator $f\otimes g:\mathcal {G}\rightarrow \mathcal {H}$,$f\in \mathcal {H}$, $g\in \mathcal {G}$, is defined as

$$\begin{aligned} (f\otimes g)h=f\langle g,h\rangle _{\mathcal {G}},\ \text {for all}\ h\in \mathcal {G}. \end{aligned}$$

This is a generalization of the cross-covariance matrix between random vectors. Moreover, by the definition of the Hilbert–Schmidt (HS) norm, we can compute the HS norm of $f\otimes g$ via

$$\begin{aligned} \Vert f\otimes g\Vert _{HS}^2=\Vert f\Vert _{\mathcal {H}}^2\Vert g\Vert _{\mathcal {G}}^2. \end{aligned}$$

Definition 9

(Hilbert–Schmidt Independence Criterion, Gretton et al. 2005) Hilbert–Schmidt Independence Criterion (HSIC) is the squared Hilbert–Schmidt norm (or Frobenius norm) of the cross-covariance operator associated with the probability measure $P_{\pmb {X},\pmb {Y}}$ on ($\mathbb {R}^p\times \mathbb {R}^q$, $\Gamma \times \Lambda$):

$$\begin{aligned} {{\mathrm{HSIC}}}(P_{\pmb {X},\pmb {Y}})=\Vert \pmb {C}_{\pmb {X},\pmb {Y}}\Vert _F^2. \end{aligned}$$

To compute it we need to express HSIC in terms of kernel functions (Gretton et al. 2005):

$$\begin{aligned} {{\mathrm{HSIC}}}(P_{\pmb {X},\pmb {Y}})&={{\mathrm{E}}}_{\pmb {X},\pmb {X'},\pmb {Y},\pmb {Y'}}[k(\pmb {X},\pmb {X}')l(\pmb {Y},\pmb {Y}')]\nonumber \\&+{{\mathrm{E}}}_{\pmb {X},\pmb {X'}}[k(\pmb {X},\pmb {X}')]{{\mathrm{E}}}_{\pmb {Y},\pmb {Y'}}[l(\pmb {Y},\pmb {Y}')]\nonumber \\&-2{{\mathrm{E}}}_{\pmb {X},\pmb {Y}}[{{\mathrm{E}}}_{\pmb {X'}}[k(\pmb {X},\pmb {X}')]{{\mathrm{E}}}_{\pmb {Y'}}[l(\pmb {Y},\pmb {Y}')]]. \end{aligned}$$

(5)

Here ${{\mathrm{E}}}_{\pmb {X},\pmb {X'},\pmb {Y},\pmb {Y'}}$ denotes the expectation over independent pairs $(\pmb {X},\pmb {Y})$ and $(\pmb {X}',\pmb {Y}')$ distributed according to $P_{\pmb {X},\pmb {Y}}$.

It follows from (5) that the Frobenius norm of $\pmb {C}_{\pmb {X},\pmb {Y}}$ exists when the various expectations over the kernels are bounded, which is true as long as the kernels k and l are bounded.

Definition 10

(Empirical HSIC, Gretton et al. 2005) Let $S=\{(\pmb x_1,\pmb y_1),\ldots ,(\pmb x_n,\pmb y_n)\}\subseteq \mathbb {R}^p\times \mathbb {R}^q$ be a series of n independent observations drawn from $P_{\pmb X,\pmb Y}$. An estimator of HSIC, written HSIC(S), is given by

$$\begin{aligned} {{\mathrm{HSIC}}}(S)=\frac{1}{n^2}\langle \pmb {K},\widetilde{\pmb {L}}\rangle _F, \end{aligned}$$

(6)

where $\pmb K = (k(\pmb x_i, \pmb x_j))$, $\pmb L = (l(\pmb y_i, \pmb y_j))\in \mathbb {R}^{n\times n}$.

Comparing (4) and (6) and using (3), we see that the centered kernel target alignment (KTA) is simply a normalized version of ${{\mathrm{HSIC}}}(S)$.

In two seminar papers on Székely et al. (2007) and Székely and Rizzo (2009) introduced the distance covariance (dCov) and distance correlation (dCor) as powerful measures of dependence.

For column vectors $\pmb {s}\in \mathbb {R}^p$ and $\pmb {t}\in \mathbb {R}^q$, denote by $\Vert \pmb {s}\Vert _p$ and $\Vert \pmb {t}\Vert _q$ the standard Euclidean norms on the corresponding spaces. For jointly distributed random vectors $\pmb {X}\in \mathbb {R}^p$ and $\pmb {Y}\in \mathbb {R}^q$, let

$$\begin{aligned} f_{\pmb {X},\pmb {Y}}(\pmb {s},\pmb {t})={{\mathrm{E}}}_{\pmb {X},\pmb {Y}}\{\exp [i\langle \pmb {s},\pmb {X}\rangle _p+i\langle \pmb {t},\pmb {Y}\rangle _q]\}, \end{aligned}$$

be the joint characteristic function of $(\pmb {X},\pmb {Y})$, and let $f_{\pmb {X}}(\pmb {s})=f_{\pmb {X},\pmb {Y}}(\pmb {s},\pmb {0})$ and $f_{\pmb {Y}}(\pmb {t})=\varphi _{\pmb {X},\pmb {Y}}(\pmb {0},\pmb {t})$ be the marginal characteristic functions of $\pmb {X}$ and $\pmb {Y}$, where $\pmb {s}\in \mathbb {R}^p$ and $\pmb {t}\in \mathbb {R}^q$. The distance covariance between $\pmb {X}$ and $\pmb {Y}$ is the nonnegative number $\nu (\pmb {X},\pmb {Y})$ defined by

$$\begin{aligned} \nu ^2(\pmb {X},\pmb {Y})=\frac{1}{C_pC_q}\int _{\mathbb {R}^{p+q}} \frac{|f_{\pmb {X},\pmb {Y}}(\pmb {s},\pmb {t})-f_{\pmb {X}}(\pmb {s})f_{\pmb {Y}}(\pmb {t})|^2}{\Vert \pmb {s}\Vert _p^{p+1}\Vert \pmb {t}\Vert _q^{q+1}}d\pmb {s}d\pmb {t}, \end{aligned}$$

and |z| denotes the modulus of $z\in \mathbb {C}$ and

$$\begin{aligned} C_p=\frac{\pi ^{\frac{1}{2}(p+1)}}{\Gamma (\frac{1}{2}(p+1))}. \end{aligned}$$

The distance correlation between $\pmb {X}$ and $\pmb {Y}$ is the nonnegative number defined by

$$\begin{aligned} \mathcal {R}(\pmb {X},\pmb {Y})=\frac{\nu (\pmb {X},\pmb {Y})}{\sqrt{\nu (\pmb {X},\pmb {X})\nu (\pmb {Y},\pmb {Y})}} \end{aligned}$$

if both $\nu (\pmb {X},\pmb {X})$ and $\nu (\pmb {Y},\pmb {Y})$ are strictly positive, and defined to be zero otherwise. For distributions with finite first moments, the distance correlation characterizes independence in that $0\le \mathcal {R}(\pmb {X},\pmb {Y})\le 1$ with $\mathcal {R}(\pmb {X},\pmb {Y})=0$ if and only if $\pmb {X}$ and $\pmb {Y}$ are independent.

Sejdinovic et al. (2013) demonstrated that distance covariance is an instance of the Hilbert–Schmidt Independence Criterion. Górecki et al. (2016, 2017) showed an extension of the distance covariance and distance correlation coefficients to the functional case.

2.4 Kernel-based independence test

Statistical tests of independence have been associated with a broad variety of dependence measures. Classical tests such as Spearman’s $\rho$ and Kendall’s $\tau$ are widely applied, however they are not guaranteed to detect all modes of dependence between the random variables. Contingency table-based methods, and in particular the power-divergence family of test statistics (Read and Cressie 1988) are the best known general purpose tests of independence, but are limited to relatively low dimensions, since they require a partitioning of the space in which random variable resides. Characteristic function-based tests (Feuerverger 1993; Kankainen 1995) have also been proposed. They are more general than kernel-based tests, although to our knowledge they have been used only to compare univariate random variables.

Now, we describe how HSIC can be used as an independence measure, and as the basis for an independence test. We begin by demonstrating that the Hilbert–Schmidt norm can be used as a measure of independence, as long as the associated RKHSs are universal.

A continuous kernel k on a compact metric space is called universal if the corresponding RKHS $\mathcal {H}$ is dense in the class of continuous functions of the space.

Denote by $\mathcal {H}$, $\mathcal {G}$ RKHSs with universal kernels k, l on the compact domains $\mathcal {X}$ and $\mathcal {Y}$ respectively. We assume without loss of generality that $\Vert f\Vert _{\infty }\le 1$ and $\Vert g\Vert _{\infty }\le 1$ for all $f\in \mathcal {H}$ and $g\in \mathcal {G}$. Then Gretton et al. (2005) proved that $\Vert \pmb {C}_{\pmb {X},\pmb {Y}}\Vert _{HS}=0$ if and only if $\pmb {X}$ and $\pmb {Y}$ are independent. Examples of universal kernels are Gaussian kernel and Laplacian kernel, while the linear kernel $k(\pmb {x},\pmb {x}')=\pmb {x}^\top \pmb {x}'$ is not universal—the corresponding HSIC tests only linear relationships, and a zero cross-covariance matrix characterizes independence only for multivariate Gaussian distributions. Working with the infinite dimensional operator with universal kernels, allows us to identify any general nonlinear dependence (in the limit) between any pair of vectors, not just Gaussians.

We recall that in this paper we use the Gaussian kernel. We now consider the asymptotic distribution of statistics (6).

We introduce the null hypothesis $H_0:\pmb {X} {\perp \!\!\!\perp } \pmb {Y}$ ($\pmb {X}$ is independent of $\pmb {Y}$, i.e., $P_{\pmb {X},\pmb {Y}}=P_{\pmb {X}}P_{\pmb {Y}}$). Suppose that we are given the i.i.d. samples $S_{\pmb {x}}=\{\pmb {x}_1,\ldots ,\pmb {x}_n\}$ and $S_{\pmb {y}}=\{\pmb {y}_1,\ldots ,\pmb {y}_n\}$ for $\pmb {X}$ and $\pmb {Y}$, respectively. Let $\widetilde{\pmb {K}}$ and $\widetilde{\pmb {L}}$ be the centered kernel matrices associated to the kernel function k and the sets $S_{\pmb {x}}$ and $S_{\pmb {y}}$, respectively. Let $\lambda _1\ge \lambda _2\ge \cdots \ge \lambda _n\ge 0$ be the eigenvalues of the matrix $\widetilde{\pmb {K}}$ and let $\pmb {v}_1,\ldots ,\pmb {v}_n$ be a set of orthonormal eigenvectors corresponding to these eigenvalues. Let $\lambda _1'\ge \lambda _2'\ge \cdots \ge \lambda _n'\ge 0$ be the eigenvalues of the matrix $\widetilde{\pmb {L}}$ and let $\pmb {v}_1',\ldots ,\pmb {v}_n'$ be a set of orthonormal eigenvectors corresponding to these eigenvalues. Let $\Lambda ={{\mathrm{diag}}}(\lambda _1,\ldots ,\lambda _n)$, $\Lambda '={{\mathrm{diag}}}(\lambda _1',\ldots ,\lambda _n')$, $\pmb {V}=(\pmb {v}_1,\ldots ,\pmb {v}_n)$ and $\pmb {V}'=(\pmb {v}_1',\ldots ,\pmb {v}_n')$. Suppose further that we have the eigenvalue decomposition (EVD) of the centered kernel matrices $\widetilde{\pmb {K}}$ and $\widetilde{\pmb {L}}$, i.e., $\widetilde{\pmb {K}}=\pmb {V}\pmb {\Lambda }\pmb {V}^\top$ and $\widetilde{\pmb {L}}=\pmb {V}'\pmb {\Lambda }'(\pmb {V}')^\top$.

Let $\pmb {\Psi }=(\pmb {\Psi }_1,\ldots ,\pmb {\Psi }_n)=\pmb {V}\pmb {\Lambda }^{1/2}$ and $\pmb {\Psi }'=(\pmb {\Psi }_1',\ldots ,\pmb {\Psi }_n')=\pmb {V}'(\pmb {\Lambda }')^{1/2}$, i.e., $\pmb {\Psi }_i=\sqrt{\lambda _i}\pmb {v}_i$, $\pmb {\Psi }_i'=\sqrt{\lambda _i'}\pmb {v}_i'$, $i=1,\ldots ,n$.

The following result is true (Zhang et al. 2011): under the null hypothesis that $\pmb {X}$ and $\pmb {Y}$ are independent, the statistic (6) has the same asymptotic distribution as

$$\begin{aligned} Z_n=\frac{1}{n^2}\sum _{i,j=1}^n\lambda _{i,n}\lambda _{j,n}'Z_{ij}^2, \end{aligned}$$

(7)

where $Z_{ij}^2$ are i.i.d. $\chi ^2_1$-distributed variables, $n\rightarrow \infty$.

Note that the data-based test statistic HSIC (or its probabilistic counterpart) is sensible to dependence/independence and therefore can be used as a test statistic. Also important is the knowledge of its asymptotic distribution. These facts inspire the following dependence/independence testing procedure. Given the sample $S_{\pmb {x}}$ and $S_{\pmb {y}}$, one first calculates the centered kernel matrices $\widetilde{\pmb {K}}$ and $\widetilde{\pmb {L}}$ and their eigenvalues $\lambda _i$ and $\lambda _i'$, and then evaluates the statistic ${{\mathrm{HSIC}}}(S)$ according to (6). Next, the empirical null distribution of Z under the null hypothesis can be simulated in the following way: one draws i.i.d. random samples from the $\chi ^2_1$-distributed variables $Z_{ij}^2$, and then generates samples for Z according to (7). Finally the p value can be found by locating ${{\mathrm{HSIC}}}(S)$ in the simulated null distribution.

A permutation-based test is described in Gretton et al. (2005). In the first step they propose to calculate the test statistic T (HSIC or KTA) for the given data. Next, keeping the order of the first sample we randomly permute the second sample a large number of times, and recompute the selected statistic each time. This destroy any dependence between samples simulating a draw from the product of marginals, making the empirical distribution of the permuted statistics behave like the null distribution of the test statistic. For a specified significance level $\alpha$, we calculate threshold $t_\alpha$ in the right tail of the null distribution. We reject $H_0$ if $T>t_\alpha$. This test was proved to be consistent against any fixed alternative. It means that for any fixed significance level $\alpha$, the power goes to 1 as the sample size tends to infinity.

2.5 Functional data

In recent years methods for representing data by functions or curves have received much attention. Such data are known in the literature as the functional data (Ramsay and Silverman 2005; Horváth and Kokoszka 2012; Hsing and Eubank 2015). Examples of functional data can be found in various application domains, such as medicine, economics, meteorology and many others. Functional data can be seen as the values of random process X(t). In practice, the values of the observed random process X(t) are always recorded at discrete times $t_1,\ldots ,t_J$, less frequently or more densely spaced in the range of variability of the argument t. So we have a time series $\{x(t_1),\ldots ,y(t_J)\}$. However, there are many reasons to model these series as elements of functional space., because the functional data has many advantages over other ways of representing the time series.

• 1. They easily cope with the problem of missing observations, an inevitable problem in many areas of research. Unfortunately, most data analysis methods require complete time series. One solution is to delete a time series that has missing values from the data, but this can lead to , and generally leads to, loss of information. Another option is to use one of many statistical methods to predict the missing values, but then the results will depend on the interpolation method. In contrast to this type of solutions, in the case of functional data, the problem of missing observations is solved by expressing time series in the form of a set of continuous functions.

• 2. The functional data naturally preserve the structure of observations, i.e. they maintain the time dependence of the observations and take into account the information about each measurement.

• 3. The moments of observations do not have to be evenly spaced in individual time series.

• 4. Functional data avoids the curse of dimensionality. When the number of time points is greater than the number of time series considered, most statistical methods will not give satisfactory results due to overparametrization. In the case of functional data, this problem can be avoided because the time series are replaced with a set of continuous functions independent of the number of time points in which observations are measured.

In most of the papers on functional data analysis, objects are characterized by only one feature observed at many time points. In several applications there is a need to use statistical methods for objects characterized by many features observed at many time points (double multivariate data). In this case, such data are transformed into multivariate functional data.

Let us assume that $\pmb {X} = (X_1,\ldots ,X_p)^\top = \{\pmb {X}(s), s\in I_1\}\in L_2^p(I_1)$ and $\pmb {Y} = (Y_1,\ldots ,Y_q)^\top = \{\pmb {Y}(t), t\in I_2\}\in L_2^q(I_2)$ are random processes, where $L_2(I)$ is a space of square integrable functions on the interval I. We also assume that

$$\begin{aligned} {{\mathrm{E}}}(\pmb {X}(s))=\pmb {0},\ s\in I_1,\quad {{\mathrm{E}}}(\pmb {Y}(t))=\pmb {0},\ t\in I_2. \end{aligned}$$

We will further assume that each component $X_g$ of the random process $\pmb {X}$ and $Y_h$ of the random process $\pmb {Y}$ can be represented by a finite number of orthonormal basis functions $\{\varphi _e\}$ and $\{\varphi _f\}$ of space $L_2(I_1)$ and $L_2(I_2)$, respectively:

$$\begin{aligned} X_g(s)&=\sum _{e=0}^{E_g}\alpha _{ge}\varphi _e(s), s\in I_1, g=1,2,\ldots ,p,\\ Y_h(t)&=\sum _{f=0}^{F_h}\beta _{hf}\varphi _f(t), t\in I_2, h=1,2,\ldots ,q, \end{aligned}$$

where $\alpha _{ge}$ and $\beta _{hf}$ are the random coefficients. The degree of smoothness of processes $X_g$ and $Y_h$ depends on the values $E_g$ and $F_h$ respectively (small values imply more smoothing). The optimum values for $E_g$ and $F_h$ are selected using Bayesian Information Criterion (BIC) (see Górecki et al. 2018). As basis functions we can use e.g. the Fourier basis system or spline functions.

We introduce the following notation:

$$\begin{aligned} \pmb {\alpha }&=(\alpha _{10},...,\alpha _{1E_1},...,\alpha _{p0},...,\alpha _{pE_p})^\top ,\\ \pmb {\beta }&=(\beta _{10},...,\beta _{1F_1},...,\beta _{q0},...,\beta _{qF_q})^\top ,\\ \pmb {\varphi }_{E_g}(s)&=(\varphi _0(s),\ldots ,\varphi _{E_g}(s))^\top , s\in I_1, g=1,2,...,p,\\ \pmb {\varphi }_{F_h}(t)&=(\varphi _0(t),\ldots ,\varphi _{F_h}(t))^\top ,\\ t\in I_2, h=1,2,...,q, \pmb {\Phi }_1(s)&= \left[ \begin{array}{cccc} \pmb {\varphi }^\top _{E_1}(s) &{} \pmb {0} &{} \ldots &{} \pmb {0} \\ \pmb {0} &{} \pmb {\varphi }^\top _{E_2}(s) &{} \ldots &{} \pmb {0} \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ \pmb {0}&{} \pmb {0} &{} \ldots &{} \pmb {\varphi }^\top _{{{\mathrm{E}}}_p}(s) \\ \end{array}\right] ,\\ \pmb {\Phi }_2(t)&= \left[ \begin{array}{cccc} \pmb {\varphi }^\top _{F_1}(t) &{} \pmb {0} &{} \ldots &{} \pmb {0} \\ \pmb {0} &{} \pmb {\varphi }^\top _{F_2}(t) &{} \ldots &{} \pmb {0} \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ \pmb {0}&{} \pmb {0} &{} \ldots &{} \pmb {\varphi }^\top _{F_q}(t) \\ \end{array}\right] , \end{aligned}$$

where $\pmb \alpha \in \mathbb {R}^{K_1 + p}$, $\pmb \beta \in \mathbb {R}^{K_2 + q}$, $\pmb \Phi _1\in \mathbb {R}^{p + (K_1 + p)},$$\pmb \Phi _2\in \mathbb {R}^{q + (K_2 + q)},$$K_1 = E_1+\cdots + E_p,$$K_2 = F_1+\cdots + F_p.$

Using the above matrix notation the random processes $\pmb {X}$ and $\pmb {Y}$ can be represented as:

$$\begin{aligned} \pmb {X}(s)=\pmb {\Phi }_1(s) \pmb {\alpha },\ s\in I_1,\ \pmb {Y}(t)=\pmb {\Phi }_2(t) \pmb {\beta },\ t\in I_2, \end{aligned}$$

(8)

where ${{\mathrm{E}}}(\pmb {\alpha })=\pmb {0}$, ${{\mathrm{E}}}(\pmb {\beta })=\pmb {0}$.

This means that the values of random processes $\pmb {X}$ and $\pmb {Y}$ are in finite dimensional subspaces of $L_2^p(I_1)$ and $L_2^q(I_2)$, respectively. We will denote these subspaces by $\mathcal {L}_2^p(I_1)$ and $\mathcal {L}_2^q(I_2)$.

Typically data are recorded at discrete moments in time. The process of transformation of discrete data to functional data is performed for each realization and each variable separately. Let $x_{gj}$ denote an observed value of the feature $X_g$, $g=1,2,\ldots p$ at the jth time point $s_j$, where $j=1,2,...,J$. Similarly, let $y_{hj}$ denote an observed value of feature $Y_h$, $h=1,2,\ldots q$ at the jth time point $t_j$, where $j=1,2,...,J$. Then our data consist of pJ pairs of $(s_{j},x_{gj})$ and of qJ pairs of $(t_{j},y_{hj})$. Let $\pmb X_1,\ldots ,\pmb X_n$ and $\pmb Y_1,\ldots ,\pmb Y_n$ be independent trajectories of random processes $\pmb X$ and $\pmb Y$ having the representation (8).

The coefficients $\pmb {\alpha }_i$ and $\pmb {\beta }_i$ are estimated by the least squares method. Let us denote these estimates by $\pmb {a}_i$ and $\pmb {b}_i$, $i=1,2,\ldots ,n$.

As a result, we obtain functional data of the form:

$$\begin{aligned} \pmb {X}_i(s)=\pmb {\Phi }_1(s)\pmb {a}_i,\ \pmb {Y}_i(t)=\pmb {\Phi }_2(t)\pmb {b}_i, \end{aligned}$$

(9)

where $s\in I_1$, $t\in I_2$, $\pmb {a}_i\in \mathbb {R}^{K_1+p}$, $\pmb {b}_i\in \mathbb {R}^{K_2+q}$, $K_1=E_1+\cdots +E_p$, $K_2=F_1+\cdots +F_q$, and $i=1,2,\ldots ,n$.

Górecki and Smaga (2017) described a multivariate analysis of variance (MANOVA) for functional data. In the paper by Górecki et al. (2018), three basic methods of dimension reduction for multidimensional functional data are given: principal component analysis, canonical correlation analysis, and discriminant coordinates.

3 Alignment for multivariate functional data

3.1 The alignment between two kernel functions and two kernel matrices for multivariate functional data

Let $\pmb {x}(s)\in \mathcal {L}_2^p(I_1)$, $s\in I_1$, where $\mathcal {L}_2^p(I_1)$ is a finite-dimensional space of continuous square-integrable vector functions over interval $I_1$.

Let

$$\begin{aligned} k^{\star }:\mathcal {L}_2^p(I_1)\times \mathcal {L}_2^p(I_1)\rightarrow \mathbb {R} \end{aligned}$$

be a kernel function on $\mathcal {L}_2^p(I_1)$. As already mentioned, in this paper we use the Gaussian kernel. For the multivariate functional data this kernel has the form:

$$\begin{aligned} k^{\star }(\pmb {x}(s),\pmb {x}'(s))=\exp (-\lambda _1\Vert \pmb {x}(s)-\pmb {x}'(s)\Vert ^2),\ \lambda _1>0. \end{aligned}$$

But from (9), and by the orthonormality of the basis functions, we have:

$$\begin{aligned} \Vert \pmb {x}(s)-\pmb {x}'(s)\Vert ^2&=\int _{I_1}(\pmb {x}(s)-\pmb {x}'(s))^\top (\pmb {x}(s)-\pmb {x}'(s))ds\\&=\Vert \pmb {a}-\pmb {a}'\Vert ^2. \end{aligned}$$

Hence

$$\begin{aligned} k^{\star }(\pmb {x}(s),\pmb {x}'(s))=k(\pmb {a},\pmb {a}') \end{aligned}$$

and

$$\begin{aligned} k^{\star }(\pmb {y}(t),\pmb {y}'(t))=k(\pmb {b},\pmb {b}'), \end{aligned}$$

where $\pmb {a}$ and $\pmb {b}$ are vectors occurring in the representation (9) of vector functions $\pmb {x}(s)$, $s\in I_1$, $\pmb {y}(t)$, $t\in I_2$.

For a given subset $\{ \pmb {x}_1(s),\ldots ,\pmb {x}_n(s) \}$ of $\mathcal {L}_2^p(I_1)$ and the given kernel function $k^{\star }$ on $\mathcal {L}_2^p(I_1)\times \mathcal {L}_2^p(I_1)$, the matrix $\pmb {K}^{\star }$ of size $n\times n$, which has its (i, j)th element $K_{ij}^{\star }(s)$, given by $K_{ij}^{\star }(s)=k^{\star }(\pmb {x}_i(s),\pmb {x}_j(s))$, $s\in I_1$, is called the kernel matrix of the kernel function $k^{\star }$ with respect to the set $\{ \pmb {x}_1(s),\ldots ,\pmb {x}_n(s) \}$, $s\in I_1$.

Definition 11

(Kernel function alignment for functional data) Let $\tilde{k}^{\star }$ and $\tilde{l}^{\star }$ be two kernel functions defined over $\mathcal {L}_2^p(I_1)\times \mathcal {L}_2^p(I_1)$ and $\mathcal {L}_2^q(I_2)\times \mathcal {L}_2^q(I_2)$, respectively, such that $0<{{\mathrm{E}}}_{\pmb {X},\pmb {X}'}[\tilde{k}^{\star ^2}(\pmb {X},\pmb {X}')]<\infty$ and $0<{{\mathrm{E}}}_{\pmb {Y},\pmb {Y}'}[\tilde{l}^{\star ^2}(\pmb {Y},\pmb {Y}')]<\infty$, where $\pmb {X},\pmb {X}'$ and $\pmb {Y},\pmb {Y}'$ are independent copies distributed according to $P_{\pmb {X}}$ and $P_{\pmb {Y}}$, respectively. Then the alignment between $\tilde{k}^{\star }$ and $\tilde{l}^{\star }$ is defined by

$$\begin{aligned} \rho (\tilde{k}^{\star },\tilde{l}^{\star }) = \frac{{{\mathrm{E}}}_{\pmb {X},\pmb {Y}}[\tilde{k}^{\star }(\pmb {X},\pmb {X}')\tilde{l}^{\star }(\pmb {Y},\pmb {Y}')]}{\sqrt{{{\mathrm{E}}}_{\pmb {X}}[\tilde{k}^{\star ^2}(\pmb {X},\pmb {X}')]{{\mathrm{E}}}_{\pmb {Y}}[\tilde{l}^{\star ^2}(\pmb {Y},\pmb {Y}')]}}. \end{aligned}$$

(10)

We can define similarly the alignment between two kernel matrices $\widetilde{\pmb {K}}^{\star }$ and $\widetilde{\pmb {L}}^{\star }$ based on the subset $\{ \pmb {x}_1(s),\ldots ,\pmb {x}_n(s) \}$, $s\in I_1$, and $\{ \pmb {y}_1(t),\ldots ,\pmb {y}_n(t) \}$, $t\in I_2$, of $\mathcal {L}_2^p(I_1)$ and $\mathcal {L}_2^q(I_2)$, respectively.

Definition 12

(Kernel matrix alignment for functional data) Let $\widetilde{\pmb {K}}^{\star }\in \mathbb {R}^{n\times n}$ and $\widetilde{\pmb {L}}^{\star }\in \mathbb {R}^{n\times n}$ be two kernel matrices such that $\Vert \widetilde{\pmb {K}}^{\star }\Vert _F\ne 0$ and $\Vert \widetilde{\pmb {L}}^{\star }\Vert _F\ne 0$. Then, the centered kernel target alignment (KTA) between $\widetilde{\pmb {K}}^{\star }$ and $\widetilde{\pmb {L}}^{\star }$ is defined:

$$\begin{aligned} \hat{\rho }(\pmb {K}^{\star },\pmb {L}^{\star })= \frac{\langle \widetilde{\pmb {K}}^{\star },\widetilde{\pmb {L}}^{\star }\rangle _F}{\Vert \widetilde{\pmb {K}}^{\star } \Vert _F \Vert \widetilde{\pmb {L}}^{\star } \Vert _F}. \end{aligned}$$

(11)

If $\widetilde{\pmb {K}}^{\star }$ and $\widetilde{\pmb {L}}^{\star }$ are positive semi-definite matrices, then $\hat{\rho }(\pmb {K}^{\star },\pmb {L}^{\star })\in [0,1]$. We have

$$\begin{aligned} \hat{\rho }(\pmb {K}^{\star },{\pmb {L}^{\star }})=\hat{\rho }(\pmb {K},\pmb {L}), \end{aligned}$$

where $\pmb {K}$ is the matrix of size $n\times n$, which has its (i, j)th element $K_{ij}$, given by $K_{ij}=k(\pmb {a}_i,\pmb {a}_j)$.

3.2 Kernel-based independence test for multivariate functional data

Definition 13

(Empirical HSIC for functional data) The empirical HSIC for functional data is defined as

$$\begin{aligned} {{\mathrm{HSIC}}}(S^{\star }) = \frac{1}{n^2}\langle \pmb K^{\star }, \pmb L^{\star }\rangle _F, \end{aligned}$$

where $S^{\star } = \{(\pmb x_1(s), \pmb y_1(t)),\ldots ,(\pmb x_n(s), \pmb y_n(t))\},\ s\in I_1, \ t\in I_2$, $\pmb K^{\star }$ and $\pmb L^{\star }$ are kernel matrices based on the subsets $\{\pmb x_1(s),\ldots , \pmb x_n(s)\}, \ s\in I_1$, and $\{\pmb y_1(t),\ldots , \pmb y_n(t)\},$$t\in I_2$ of $\mathcal {L}_2^p(I_1)$ and $\mathcal {L}_2^q(I_2)$, respectively.

But $\pmb K^{\star } = \pmb K$, where $\pmb K$ is the kernel matrix of size $n\times n$, which has its (i, j)th element $K_{ij}$ given by $K_{ij} = k(\pmb a_i, \pmb a_j)$, where $\pmb a_1,\ldots ,\pmb a_n$ are vectors occurring in the representation (9) vector functions $\pmb X(s), \ s\in I_1$. Analogously, $\pmb L^{\star } = \pmb L$, where $\pmb L$ is the kernel matrix of size $n\times n$, which has its (i, j)th element $L_{ij}$ given by $L_{ij} = l(\pmb b_i, \pmb b_j)$, where $\pmb b_1,\ldots ,\pmb b_n$ are vectors occurring in the representation (9) vector functions $\pmb Y(t), \ t\in I_2$. Hence

$$\begin{aligned} {{\mathrm{HSIC}}}(S^{\star }) = {{\mathrm{HSIC}}}(S_v), \end{aligned}$$

where $S_v = \{(\pmb a_1, \pmb b_1),\ldots ,(\pmb a_n, \pmb b_n)\}$.

Note also that the null hypothesis $H_0:\pmb {X} \bot \pmb {Y}$ of independence of the random processes $\pmb {X}$ and $\pmb {Y}$ is equivalent to the null hypothesis $H_0:\pmb {\alpha } \bot \pmb {\beta }$ of independence of random vectors $\pmb {\alpha }$ and $\pmb {\beta }$ occurring in the representation (8) random processes $\pmb {X}$ and $\pmb {Y}$. We can therefore use the tests described in Section 2.4, replacing $\pmb {x}$ and $\pmb {y}$ by $\pmb {a}$ and $\pmb {b}$.

3.3 Canonical correlation analysis based on the alignment between kernel matrices for multivariate functional data

In classical canonical correlation analysis (Hotelling 1936), we are interested in the relationship between two random vectors $\pmb {X}$ and $\pmb {Y}$. In the functional case we are interested in the relationship between two random functions $\pmb {X}$ and $\pmb {Y}$. Functional canonical variables U and V for random processes $\pmb {X}$ and $\pmb {Y}$ are defined as follows

$$\begin{aligned} U&= \langle \pmb {u},\pmb {X}\rangle =\int _{I_1}\pmb {u}^\top (s)\pmb {X}(s)ds, \end{aligned}$$

(12)

$$\begin{aligned} V&= \langle \pmb {v},\pmb {Y}\rangle =\int _{I_2}\pmb {v}^\top (t)\pmb {Y}(t)dt, \end{aligned}$$

(13)

where the vector functions $\pmb {u}$ and $\pmb {v}$ are called the vector weight functions and are of the form

$$\begin{aligned} \pmb {u}(s)=\pmb {\Phi }_1(s) \pmb {u},\ \pmb {v}(t)=\pmb {\Phi }_2(t) \pmb {v}\ \text {where}\ \pmb {u}\in \mathbb {R}^{K_1 + p}, \pmb {v}\in \mathbb {R}^{K_2 + q}. \end{aligned}$$

(14)

Classically the weight functions $\pmb {u}$ and $\pmb {v}$ are chosen to maximize the sample correlation coefficient (Górecki et al. 2018):

$$\begin{aligned} \rho =\frac{{{\mathrm{Cov}}}(U,V)}{\sqrt{{{\mathrm{Var}}}(U){{\mathrm{Var}}}(V)}}. \end{aligned}$$

(15)

The sample correlation coefficient between the variables U and V is now replaced by a centered kernel target alignment (KTA) between kernel matrices $\pmb {K}$ and $\pmb {L}$ based on the projected data $\langle \pmb {u}(s),\pmb {x}_i(s)\rangle _{\mathcal {H}}$ and $\langle \pmb {v}(t),\pmb {y}_i(t)\rangle _{\mathcal {H}}$, i.e. their (i, j)th entry are

$$\begin{aligned} K_{i,j}=k(\langle \pmb {u}(s),\pmb {x}_i(s)\rangle _{\mathcal {H}},\langle \pmb {u}(s),\pmb {x}_j(s)\rangle _{\mathcal {H}}), s\in I_1, \end{aligned}$$

and

$$\begin{aligned} L_{i,j} = l(\langle \pmb {v}(t),\pmb {y}_i(t)\rangle _{\mathcal {H}},\langle \pmb {v}(t),\pmb {y}_j(t)\rangle _{\mathcal {H}}), t\in I_2, \end{aligned}$$

respectively, $i,j=1,\ldots ,n$:

$$\begin{aligned} \hat{\rho }(\pmb {u}(s),\pmb {v}(t)) = \frac{{{\mathrm{tr}}}(\widetilde{\pmb {K}}^\top \widetilde{\pmb {L}})}{\sqrt{{{\mathrm{tr}}}(\widetilde{\pmb {K}}^\top \widetilde{\pmb {K}}) {{\mathrm{tr}}}(\widetilde{\pmb {L}}^\top \widetilde{\pmb {L}})}} \end{aligned}$$

(16)

subject to

$$\begin{aligned} \Vert \pmb {u}(s)\Vert =\Vert \pmb {v}(t)\Vert =1. \end{aligned}$$

(17)

But

$$\begin{aligned} \pmb {K}_{i,j}&= k\left( \int _{I_1}\pmb {u}^\top (s)\pmb {x}_i(s)ds,\int _{I_1}\pmb {u}^\top (s)\pmb {x}_j(s)ds\right) \\&=k(\pmb {u}^\top \pmb {a}_i,\pmb {u}^\top \pmb {a}_j)=\pmb {K}_{i,j}^{(\pmb {u})} \end{aligned}$$

and

$$\begin{aligned} \pmb {L}_{i,j}&= l\left( \int _{I_2}\pmb {v}^\top (t)\pmb {y}_i(t)dt,\int _{I_2}\pmb {v}^\top (t)\pmb {y}_j(t)dt\right) \\&=l(\pmb {v}^\top \pmb {b}_i,\pmb {v}^\top \pmb {b}_j)=\pmb {L}_{i,j}^{(\pmb {v})}, \end{aligned}$$

where $\pmb {a}_i$ and $\pmb {b}_i$ are vectors occuring in the representation (9) vectors functions $\pmb {x}(s)$, $s\in I_1$, $\pmb {y}(t)$, $t\in I_2$, $i=1,\ldots ,n$, $\pmb {u}\in \mathbb {R}^{K_1+p}$, $\pmb {v}\in \mathbb {R}^{K_2+q}$.

Thus, the choice of weighting functions $\pmb {u}(s)$ and $\pmb {v}(t)$ so that the coefficient (16) has a maximum value subject to (17) is equivalent to the choice of vectors $\pmb {u}\in \mathbb {R}^{K_1+p}$ and $\pmb {v}\in \mathbb {R}^{K_2+q}$ such that the coefficient

$$\begin{aligned} \hat{\rho }(\pmb {u},\pmb {v})=\frac{{{\mathrm{tr}}}(\widetilde{\pmb {K}}_{\pmb {u}}^\top \widetilde{\pmb {L}}_{\pmb {v}})}{\sqrt{{{\mathrm{tr}}}(\widetilde{\pmb {K}}_{\pmb {u}}^\top \widetilde{\pmb {K}}_{\pmb {u}}) {{\mathrm{tr}}}(\widetilde{\pmb {L}}_{\pmb {v}}^\top \widetilde{\pmb {L}}_{\pmb {v}})}} \end{aligned}$$

(18)

has a maximum value subject to

$$\begin{aligned} \Vert \pmb {u}\Vert =\Vert \pmb {v}\Vert =1, \end{aligned}$$

(19)

where $\pmb {K}_{\pmb {u}}=(K_{i,j}^{(\pmb {u})})$, $\pmb {L}_{\pmb {v}}=(L_{i,j}^{(\pmb {v})})$, $i,j=1,\ldots ,n$.

In order to maximize the coefficient of (18) we can use the result of Chang et al. (2013). Authors used a gradient descent algorithm, with modified gradient to ensure the unit length constraint is satisfied at each step (Edelman et al. 1998). Optimal step-sizes were found numerically using the Nelder-Mead method. This article employs the Gaussian kernel exclusively while other kernels are available. The bandwidth parameter $\lambda$ of the Gaussian kernel was chosen using the “median trick” (Song et al. 2010), i.e. the median Euclidean distance between all pairs of points.

The coefficients of the projection of the ith value $\pmb {x}_i(t)$ of random process $\pmb {X}$ on the kth functional canonical variable are equal to

$$\begin{aligned} \hat{U}_{ik}=\langle \pmb {u}_k,\pmb {x}_i\rangle =\int _{I_1}\pmb {u}_k^\top (s)\pmb {x}_i(s)ds=\pmb {a}_i^\top \pmb {u}_k, \end{aligned}$$

analogously the coefficients of the projection of the ith value $\pmb {y}_i(t)$ of random process $\pmb {Y}_t$ on the kth functional canonical variable are equal to

$$\begin{aligned} \hat{V}_{ik}=\pmb {b}_i^\top \pmb {v}_k, \end{aligned}$$

where $i=1,\ldots ,n$, $k=1,\ldots ,\min ({{\mathrm{rank}}}(\pmb {A}),{{\mathrm{rank}}}(\pmb {B}))$, where $\pmb {A}\in \mathbb {R}^{n\times p}$ and $\pmb {B}\in \mathbb {R}^{n\times q}$, where the ith rows are $\pmb {a}_i$ and $\pmb {b}_i$, respectively, which have column means of zero.

As we mentioned earlier KTA is a normalized variant of HSIC. Hence, we can repeat the above reasoning for HSIC criterion. However, we should remember that both approaches are not equivalent and we can obtain different results.

4 Experiments

Let us recall some and introduce another symbols:

• KTA—centered kernel target alignment,

• HSIC—Hilbert–Schmidt Independence Criterion,

• FCCA—classical functional canonical correlation analysis (Ramsay and Silverman 2005; Horváth and Kokoszka 2012),

• HSIC.FCCA—functional canonical correlation analysis based on HSIC,

• HSIC.KTA—functional canonical correlation analysis based on KTA.

4.1 Simulation

We generated random processes along with some noises to test the performance of the introduced measures. Random processes are specified by

$$\begin{aligned} X_t&=\varepsilon _{t},\\ Y_t&= 3X_t + \eta _{t},\\ Z_t&= X_t^2 + \xi _{t}, \end{aligned}$$

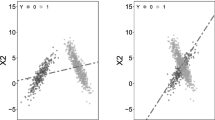
where $\varepsilon _t,$$\eta _t$ and $\xi _t$ are jointly independent random variables from Gaussian distribution with 0 mean and 0.25 variance. We generated processes of length 100. $N = 10000$ samples are generated for all processes. The objective is to examine how well functional variants (Fourier basis with 15 basis functions) of KTA and HSIC measures perform compared to measures used on raw data (artificially generated at discrete time stamps). Here, raw data are represented as vector data of generated trajectories, so raw data are three 10000 by 100 dimensional matrices(one for $X_t$, second for $Y_t$ and third for $Z_t$). On the other hand, functional data are three 10000 by 15 dimensional matrices (coefficients of Fourier basis). Here, $X_t$ and $Y_t$ are linearly dependent, whereas $X_t$, $Z_t$ and $Y_t$, $Z_t$ are nonlinearly dependent (Fig. 1).

Fig. 1

Sample trajectories of $X_t$, $Y_t$ and $Z_t$ time series for raw (left plot) and functional (right plot) representation

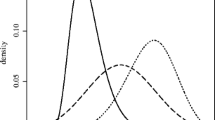
From Fig. 2 and Table 1, we see that the proposed extension of HSIC and KTA coefficients to functional data gives larger values of coefficients than the variants for raw time series. Unfortunately, it is not possible to perform inference based only on the values of coefficients. We have to apply tests. In Fig. 3 and in Table 2, we observe that when we use functional variants of the proposed measures, we obtain much better results in recognizing nonlinear dependence. Linear dependence between $X_t$ and $Y_t$ was easily recognized by each method (100% of correct decisions—p values below 5%). Results of functional KTA and HSIC are very similar. Non-functional measures HSIC and KTA give only 7.2% and 6.7% correct decisions (p values below 5%) for relationship $X_t$, $Z_t$ and $Y_t$, $Z_t$, respectively. On the other hand, functional variants recognize dependency (p values below 5%) in 63.3% (both measures) for $X_t, Y_t$ and in 47.8% (HSIC), 63.3% (KTA) for $Y_t$, $Z_t$.

Fig. 2

Raw and functional HSIC and KTA coefficients for artificial time series

Table 1 Average raw and functional HSIC and KTA coefficients for artificial time series (number in brackets means standard deviation)

Fig. 3

p Values from permutation-based tests for raw and functional variants of HSIC and KTA coefficients

Table 2 Average p values from permutation-based tests for raw and functional variants of HSIC and KTA coefficients (number in brackets means standard deviation)

4.2 Univariate example

As a first real example we used average daily temperature (in Celsius degrees) for each day of the year and average daily rainfall (in mm) for each day of the year rounded to 0.1 mm at 35 different weather stations in Canada from 1960 to 1994. Each station belongs to one of four climate zone: Arctic (3 stations—blue color on plots), Atlantic (15—red color on plots), Continental (12— black color on plots) or Pacific (5—green color on plots) zone (Fig. 4). This data set comes from Ramsay and Silverman (2005).

Fig. 4

Location of Canadian weather stations

In the first step, we smoothed data. We used the Fourier basis with various values of the smoothing parameter (number of basis functions) from 3 to 15. We can observe the effect of smoothing in Figs. 5 and 6 (for Fourier basis with 15 basis functions). We decided to use the Fourier basis for two reasons: it has excellent computational properties, especially if the observations are equally spaced, and it is natural for describing periodic data, such as the annual weather cycles. Here, raw data are two 35 by 100 dimensional matrices (one for temperature and second for precipitation). On the other hand, functional data are two 35 by 15 dimensional matrices (coefficients of Fourier basis).

Fig. 5

Raw and functional temperature for Canadian weather stations

Fig. 6

Raw and functional precipitation for Canadian weather stations

From the plots we can observe that the level of smoothness seems big enough. Additionally, we can observe some relationship between average temperature and precipitation. Namely, for weather stations with large average temperature, we observe relatively bigger average precipitation while for Arctic stations with lowest average temperatures we observe the smallest average precipitation. So we can expect some relationship between average temperature and average precipitation for Canadian weather stations.

In the next step, we calculated the values of described earlier coefficients, the values of which are presented in Fig. 8. We observe quite big values of HSIC and KTA, but it is impossible to infer dependency from these values. We see that the values of HSIC and KTA coefficients are stable (both do not depend on basis size).

To statistically confirm the association between temperature and precipitation we performed some simulation study. This study based on Chang et al. (2013) simulation. Finding a good nonlinear dependency measure is not trivial. KTA and HSIC are not on the same scale. As Chang et al. (2013) we used Spearman correlation coefficient. We performed 50 random splits with the inclusion of 25 samples to identify models. The Spearman correlation coefficient was then calculated using the remaining 10 samples for each of 50 splits. As we know the strongest signal between the temperature and precipitation for Canadian weather stations is nonlinear (Chang et al. 2013). From Fig. 7 we can observe that HSIC.FCCA and KTA.FCCA have produced larger absolute Spearman coefficients than FCCA. Such results suggest that HSIC.FCCA & KTA.FCCA can be viewed as natural nonlinear extensions of CCA also in the case of multivariate functional data.

Fig. 7

Absolute Spearman correlation coefficient for the first set of functional canonical variables

Finally, we performed permutation-based tests for HSIC and KTA coefficients. The results are presented in Fig. 8. All tests rejected $H_0$ (p values close to 0) for all basis sizes, so we can infer that we have some relationship between average temperature and average precipitation for Canadian weather stations. Unfortunately, we know nothing about the strength and direction of the dependency. Only a visual inspection of the plots suggests that there is a strong and positive relationship.

Fig. 8

HSIC and KTA coefficients and p values of permutation-based tests for Canadian weather data

The relative positions of the 35 Canadian weather stations in the system $(\hat{U}_1,\hat{V}_1)$ of functional canonical variables are shown in Fig. 9. It seems that for both coefficients the weather stations group reasonably.

Fig. 9

Projection of the 35 Canadian weather stations on the plane ($\hat{U}_1,\hat{V}_1$)

4.3 Multivariate example

The described method was employed here to cluster the twelve groups (pillars) of variables of 38 European countries in the period 2008-2015. The list of countries used in the dependency analysis is contained in Table 3. Table 4 describes the pillars used in the analysis. For this purpose, use was made of data published by the World Economic Forum (WEF) in its annual reports (http://www.weforum.org). Those are comprehensive data, describing exhaustively various socio-economic conditions or spheres of individual states (Górecki et al. 2016). The data were transformed into functional data. Calculations were performed using the Fourier basis. In view of a small number of time periods $(J=7)$, for each variable the maximum number of basis components was taken to be equal to five. Here, raw data are twelve matrices (one for each pillar). Dimensions of matrices are different and depend on the number of variables in the pillar. Eg. for the first pillar we have 16 (number of variables) * 7 (number of time points) = 112 columns, hence dimensionality of the matrix for this pillar is 38 by 112. Similarly for the others. On the other hand, functional data are twelve matrices with 38 rows and appropriate number of columns (coefficients of Fourier basis). Number of columns for functional data eg. for the first pillar we calculate as 16 (number of variables) * 5 (number of basis elements) = 80.

Table 3 Countries used in analysis, 2008–2015

Table 4 Pillars used in analysis, 2008–2015

Tables 5 and 6 contain the values of functional HSIC and KTA coefficients. As expected, they are all close to one. But high values of these coefficients do not necessarily mean that there is a significant relationship between the two groups of variables. We can expect association between groups of pillars. However, it is really hard to guess what groups are associated.

Table 5 Functional HSIC coefficients

Table 6 Functional KTA coefficients

Similarly to the Canadian weather example we performed small simulation study for pillars G5 and G6. From Fig. 10 we can observe that HSIC.FCCA and KTA.FCCA have produced larger absolute Spearman coefficients than FCCA. This result suggest that proposed measures have better characteristic in discovering nonlinear relationship for this example.

Fig. 10

Absolute Spearman correlation coefficient for the first set of functional canonical variables for pillars G5 & G6

We performed permutation-based tests for the HSIC and KTA coefficients discussed above. For most of tests, p values were close to zero, on the basis of which it can be inferred that there is some significant relationship between the groups (pillars) of variables. Table 7 contains the p values obtained for each test. We have exactly the same p values for both methods. Now, we can observe that some groups are independent ($\alpha =0.05$): G1 & G3, G3 & G6, G3 & G8, G3 & G11, G3 & G12, G4 & G9.

The graphs of the components of the vector weight function for the first functional canonical variables of the processes are shown in Fig. 11. From Fig. 11 (left) it can be seen that the greatest contribution in the structure of the first functional canonical correlation ($U_1$) comes from “black” process, and this holds for all of the observation years considered. Figure 11 (right) shows that, on specified time intervals, the greatest contribution in the structure of the first second functional canonical correlation ($V_1$ comes alternately from the processes “black” and “red dotted”. The total contribution of a particular original process in the structure of a given functional canonical correlation is equal to the area under the module weighting function corresponding to this process. These contributions for the components are given in Table 8.

Table 7 Functional HSIC & KTA p values permutation-based tests (only non-zero)

Fig. 11

Weight functions for first functional canonical variable $U_1$ (left) and $V_1$ (right)

Figure 12 contains the relative positions of the 38 European countries in the system $(\hat{U}_1,\hat{V}_1)$ of functional canonical variables for selected groups of variables. The high correlation of the first two functional canonical variables can be seen in Fig. 12 for two pillars G5 and G6. For KTA criterion, the countries with the highest value of functional canonical variables $U_1$ and $V_1$ are: Finland (FI), France (FR), Hungary (HU), Greece (GR), Estonia (EE), Germany (DE), Iceland (IS), Czech Republic (CZ) and Denmark (DK). The countries with the lowest value of functional canonical variables $U_1$ and $V_1$ are: Romania (RO), Poland (PL), Norway (NO), Portugal (PT), Netherlands (NL) and Russian Federation (RU). Other countries belong to the intermediate group.

Table 8 Sorted areas under module weighting functions

Fig. 12

Selected projections of the 38 European countries on the plane ($\hat{U}_1,\hat{V}_1$). Regions used for statistical processing purposes by the United Nations Statistics Division: blue square—Northern Europe, cyan square—Western Europe, red square—Eastern Europe, green square—Southern Europe. (Color figure online)

During the numerical calculation process we used R software (R Core Team 2018) and packages fda (Ramsay et al. 2018) and hsicCCA (Chang 2013).

5 Conclusions

We proposed an extension of two dependency measures for two sets of variables for multivariate functional data. We proposed to use tests to examine the significance of results because the values of proposed coefficients are rather hard to interpret. Additionally, we presented the methods of constructing nonlinear canonical variables for multivariate functional data using HSIC and KTA coefficients. Tested on two real examples, the proposed method has proven useful in investigating the dependency between two sets of variables. Examples confirm usefulness of our approach in revealing the hidden structure of co-dependence between groups of variables.

During the study of proposed coefficients we discovered that the size of basis (smoothing parameter) is rather unimportant, the values (and p values for tests) do not depend on the basis size.

Of course, the performance of the methods needs to be further evaluated on additional real and artificial data sets. Moreover, we can examine the behavior of coefficients (and tests) for different bases like B-splines or wavelets (when data are not periodic, the Fourier basis could fail). This constitutes the direction of our future research.