Skip to main content

Advertisement

SpringerLink
Log in

A Mathematical Model for the Transmission Dynamics of Lymphatic Filariasis with Intervention Strategies

  • Regular Article
  • Published:
Acta Biotheoretica Aims and scope Submit manuscript

Abstract

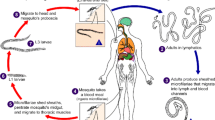
This manuscript considers the transmission dynamics of lymphatic filariasis with some intervention strategies in place. Unlike previously developed models, our model takes into account both the exposed and infected classes in both the human and mosquito populations, respectively. We also consider vaccinated, treated and recovered humans in the presented model. The global dynamics of the proposed model are completely determined by the basic (\({\mathcal {R}}_0\)) and effective reproduction numbers (\({\mathcal {R}}_e\)). We then use Lyapunov function theory to find the sufficient conditions for global stability of both the disease-free equilibrium and endemic equilibrium. The Lyapunov functions show that when the basic reproduction number is less than or equal to unity, the disease-free equilibrium is globally asymptotically stable, and when it is greater than unity then the endemic equilibrium is also globally asymptotically stable. Finally, numerical simulations are carried out to investigate the effects of the intervention strategies and key parameters to the spread of lymphatic filariasis. The numerical simulations support the analytical results and illustrate possible model behavioral scenarios.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Allen LJS (2007) An introduction to mathematical biology. Pearson Education Ltd, New York

    Google Scholar 

  • Anderson RM, May RM (1992) Infectious disease of humans: dynamics and control. Oxford University Press, London

    Google Scholar 

  • Behm CA, Bending MM, McCarter JP, Sluder AE (2003) WHO/TDR scientific working group on RNA interference as a means of identifying drug targets for filariasis’ report. WHO report. http://www.who.int/tdr/publications/documents/rna-drug.pdf

  • Bhunu CP, Mushayabasa S (2012) Transmission dynamics of lymphatic filariasis. ISRN Biomath 2012(930130):1–9

    Article  Google Scholar 

  • CDC (2013) Lymphatic filariasis. http://www.cdc.gov/parasites/lymphaticfilariasis/treatment.html. Accessed 21 Aug 2015

  • Center Carter (2015) Lymphatic filariasis elimination program. https://www.cartercenter.org/health/lf/index.html. Accessed 6 May 2015

  • Chan MS, Srividya A, Norman RA, Pani SP, Ramaiah KD, Vanamail P, Michael E, Das PK, Bundy DAP (1994) EPIFIL: a dynamic model of infection and disease in lymphatic filariasis. Am J Trop Med Hyg 59(4):606–614

    Article  Google Scholar 

  • Chitnis N, Hyman JM, Cushing JM (2008) Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull Math Biol 70:1272–1296

    Article  Google Scholar 

  • End Fund (2015) Lymphatic filariasis. Ending neglected disease.https://end.org/ntds-in-focus/lymphatic-filariasis/. Accessed 6 May 2015

  • Khan Y (2009) An effective modification of the Laplace decomposition method for nonlinear equations. Nonlinear Sci Numer Simult 10:1373–1376

    Google Scholar 

  • Labadin J, Kon CML, Juan SES (2009) Deterministic malaria transmission model with acquired immunity. In: Proceedings of world congress on engineering and computer science

  • LaSalle JP (1976) The stability of dynamic systems. SIAM, Philadelphia

    Book  Google Scholar 

  • Lashari AA, Zaman G (2011) Global dynamics of vector-borne diseases with horizontal transmission in host population. Comput Math Appl 61(4):745–754

    Article  Google Scholar 

  • Luz PM, Struchiner CJ, Galvani AP (2010) Modeling transmission dynamics and control of vector-borne neglected tropical diseases. PLoS Negl Trop Dis 4(10):e761

    Article  Google Scholar 

  • Makinde OD (2007) Adomian decomposition approach to SIR epidemic model with constant vaccination strategy. Appl Math Comput 184:842–848

    Google Scholar 

  • Michael E, Malecela-Lazaro MN, Simonsen PE, Pedersen EM, Barker G, Kumar A, Kazura JW (2004) Mathematical modeling and the control of lymphatic filariasis. LANCET Infect Dis 4(4):223–234

    Article  Google Scholar 

  • Mtisi E, Rwezaura H, Tchuenche JM (2009) A mathematical analysis of malaria tuberculosis co-dynamics. Discr Cont Dyn Syst Series B 12(4):827–864

    Google Scholar 

  • Mwamtobe PM, Abelman S, Tchuenche JM, Kasambara A (2014) Optimal (control of) intervention strategies for malaria epidemic in Karonga District, Malawi. Abst Appl Anal 2014(594256):1–20

    Google Scholar 

  • Mwamtobe PM, Simelane SM, Abelman S, Tchuenche JM (2017) Mathematical analysis of a lymphatic filariasis model with quarantine and treatment. BMC Public Health 17:265. https://doi.org/10.1186/s12889-017-4160-8

    Article  Google Scholar 

  • Mwamtobe PM, Simelane SM, Abelman S, Tchuenche JM (2018) Optimal control of intervention strategies in malaria-tubercolosis co-infection with relapse. Biomathematics 11(2):1850017

    Article  Google Scholar 

  • Norman RA, Chan MS, Srividya A, Pani SP, Ramaiah KD, Vanamail P, Michael E, Das PK, Bundy DAP (2000) EPIFIL: the development of an age-structured model for describing the transmission dynamics and control of lymphatic filariasis. Epidemiol Infect 124(3):529–541

    Article  Google Scholar 

  • Okosun KO, Ouifki R, Marcus N (2011) Optimal control analysis of a malaria disease transmission model that includes treatment and vaccination with waning immunity. Biosystems 106(2–3):136–145

    Article  Google Scholar 

  • Ottesen EA, Duke BOL, Behbehani K (1997) Strategies and tolls for the control/elimination of the lymphatic filariasis. Bull WHO 75(6):491–503

    Google Scholar 

  • Supriantna AK, Anggriani N (2012) Lymphatic filariasis transmission and control: a mathematical modelling approach. In: In: Alfonso JR-M, ed. Book chapter in Current Tropics in Tropical Medicine, pp 425–442, ISBN: 978-953-51-0274-8

  • Swaminathan S, Pan SP, Rengachari R, Kaliannagounder K, Pradeep DK (2008) Mathematical models for lymphatic filariasis transmission and control: challenges and prospects. BioMed Central 1(2):1–9

    Google Scholar 

  • Tasman H, Supali T, Suprianta AK, Nuraini N, Soewono E (2015) A mathematical model for long-term effect of diethylcarbamazine–albendazole mass drug administration on lymphatic filariasis. AIP Conf Proc 1651:138–146

    Article  Google Scholar 

  • Tewa JJ, Dimi JL, Bowong S (2009) Lyapunov function for dengue disease transmission model. Chaos Solitons Fract 39(2):936–941

    Article  Google Scholar 

  • van de Driessche P, Watmough J (2002) Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48

    Article  Google Scholar 

  • Wolfram Research, Inc (2012) Mathematica Version 9.0, Champaign

  • World Health Organization (2015) Lymphatic filariasis. https://www.who.int/lymphatic_filariasis/en/. Accessed May 2015

Download references

Acknowledgements

The reviewers are thanked for their careful reading of our manuscript. Their useful comments have resulted in an improved manuscript.

Author information

Authors and Affiliations

  1. Department of Mathematics and Applied Mathematics, University of Johannesburg, Auckland Park, 2006, South Africa

    S. M. Simelane

  2. Department of Applied Studies, Malawi Institute of Technology, Malawi University of Science and Technology, P. O. Box 5196, Limbe, Malawi

    P. M. Mwamtobe

  3. School of Computer Science and Applied Mathematics, University of the Witwatersrand, Johannesburg, Private Bag 3, Wits, 2050, South Africa

    S. Abelman & J. M. Tchuenche

Authors
  1. S. M. Simelane
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. M. Mwamtobe
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Abelman
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. J. M. Tchuenche
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. M. Simelane.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This document is a collaborative effort.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Simelane, S.M., Mwamtobe, P.M., Abelman, S. et al. A Mathematical Model for the Transmission Dynamics of Lymphatic Filariasis with Intervention Strategies. Acta Biotheor 68, 297–320 (2020). https://doi.org/10.1007/s10441-019-09370-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10441-019-09370-y

Keywords

Search

Navigation