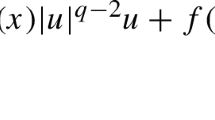Skip to main content
SpringerLink
Log in

Superlinear Elliptic Equations with Variable Exponent via Perturbation Method

  • Published:
Acta Applicandae Mathematicae Aims and scope Submit manuscript

Abstract

We are concerned with the following \(p(x)\)-Laplacian equations in \(\mathbb{R}^{N}\)

$$ -\triangle _{p(x)} u+|u|^{p(x)-2}u= f(x,u)\quad \mbox{in } \mathbb{R} ^{N}. $$

The nonlinearity is superlinear but does not satisfy the Ambrosetti-Rabinowitz type condition. Our main difficulty is that the weak limit of (PS) sequence is not always the weak solution of this problem. To overcome this difficulty, by adding potential term and using mountain pass theorem, we get the weak solution \(u_{\lambda }\) of perturbation equations. First, we prove that \(u_{\lambda }\rightharpoonup u\) as \(\lambda \rightarrow 0\). Second, by using vanishing lemma, we get that \(u\) is a nontrivial solution of the original problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Zhikov, V.V.: Averaging of functionals of the calculus of variations and elasticity theory. Math. USSR, Izv. 9, 33–66 (1987)

    MATH  Google Scholar 

  2. Ruzicka, M.: Electrorheological Fluids: Modeling and Mathematical Theory. Springer, Berlin (2000)

    MATH  Google Scholar 

  3. Chen, Y., Levine, S., Rao, M.: Variable exponent linear growth functionals in image restoration. SIAM J. Appl. Math. 66, 1383–1406 (2006)

    MathSciNet  MATH  Google Scholar 

  4. Antontsev, S.N., Shmarev, S.I.: A model porous medium equation with variable exponent of nonlinearity: existence uniqueness and localization properties of solutions. Nonlinear Anal. 60, 515–545 (2005)

    MathSciNet  MATH  Google Scholar 

  5. Antontsev, S.N., Rodrigues, J.F.: On stationary thermo-rheological viscous flows. Ann. Univ. Ferrara, Sez. 7: Sci. Mat. 52, 19–36 (2006)

    MathSciNet  MATH  Google Scholar 

  6. Zhou, Q.M., Ge, B.: The fibering map approach to a nonlocal problem involving \(p(x)\)-Laplacian. Comput. Math. Appl. 75, 632–642 (2018)

    MathSciNet  MATH  Google Scholar 

  7. Ge, B., Zhou, Q.M.: Multiple solutions for a Robin-type differential inclusion problem involving the \(p(x)\)-Laplacian. Math. Methods Appl. Sci. 40, 6229–6238 (2017)

    MathSciNet  MATH  Google Scholar 

  8. Ge, B.: Existence theorem for Dirichlet problem for differential inclusion driven by the \(p(x)\)-Laplacian. Fixed Point Theory 17, 267–274 (2016)

    MathSciNet  MATH  Google Scholar 

  9. Yucedag, Z.: Solutions of nonlinear problems involving \(p(x)\)-Laplacian operator. Adv. Nonlinear Anal. 4, 285–293 (2015)

    MathSciNet  MATH  Google Scholar 

  10. Zhou, Q.M.: On the superlinear problems involving \(p(x)\)-Laplacian-like operators without AR-condition. Nonlinear Anal., Real World Appl. 21, 161–169 (2015)

    MathSciNet  MATH  Google Scholar 

  11. Heidarkhani, S., Afrouzi, G.A., Moradi, S., Caristi, G., Ge, B.: Existence of one weak solution for \(p(x)\)-biharmonic equations with Navier boundary conditions. Z. Angew. Math. Phys. 67, 73 (2016)

    MathSciNet  MATH  Google Scholar 

  12. Cencelj, M., Radulescu, V., Repovs, D.: Double phase problems with variable growth. Nonlinear Anal. 177, 270–287 (2015)

    MathSciNet  MATH  Google Scholar 

  13. Kefi, K., Radulescu, V.: On a \(p(x)\)-biharmonic problem with singular weights. Z. Angew. Math. Phys. 68, 80 (2017)

    MathSciNet  MATH  Google Scholar 

  14. Radulescu, V.: Nonlinear elliptic equations with variable exponent: old and new. Nonlinear Anal. 121, 336–369 (2015)

    MathSciNet  MATH  Google Scholar 

  15. Gasinski, L., Papageorgiou, N.S.: A pair of positive solutions for the Dirichlet \(p(z)\)-Laplacian with concave and convex nonlinearities. J. Glob. Optim. 56, 1347–1360 (2013)

    MathSciNet  MATH  Google Scholar 

  16. Liu, J.J., Pucci, P., Wu, H.T., Zhang, Q.H.: Existence and blow-up rate of large solutions of \(p(x)\)-Laplacian equations with gradient terms. J. Math. Anal. Appl. 457, 944–977 (2018)

    MathSciNet  MATH  Google Scholar 

  17. Zhang, Q.H., Radulescu, V.: Double phase anisotropic variational problems and combined effects of reaction and absorption terms. J. Math. Pures Appl. 118, 159–203 (2018)

    MathSciNet  MATH  Google Scholar 

  18. Shi, X.Y., Radulescu, V., Repovs, D., Zhang, Q.H.: Multiple solutions of double phase variational problems with variable exponent. Adv. Calc. Var. https://doi.org/10.1515/acv-2018-0003

  19. Fan, X.L., Han, X.Y.: Existence and multiplicity of solutions for \(p(x)\)-Laplacian equations in \(\mathbb{R}^{N}\). Nonlinear Anal. 59, 173–188 (2004)

    MathSciNet  MATH  Google Scholar 

  20. Alves, C.O., Liu, S.: On superlinear \(p(x)\)-Laplacian equations in \(\mathbb{R}^{N}\). Nonlinear Anal. 73, 2566–2579 (2010)

    MathSciNet  MATH  Google Scholar 

  21. Ge, B., Zhou, Q.M., Xue, X.P.: Infinitely many solutions for a differential inclusion problem in \(\mathbb{R}^{N}\) involving \(p(x)\)-Laplacian and oscillatory terms. Z. Angew. Math. Phys. 63, 691–711 (2012)

    MathSciNet  MATH  Google Scholar 

  22. Ge, B., Liu, L.L.: Infinitely many solutions for differential inclusion problems in \(\mathbb{R}^{N}\) involving the \(p(x)\)-Laplacian. Z. Angew. Math. Phys. 67, 8 (2016)

    MATH  Google Scholar 

  23. Pucci, P., Zhang, Q.H.: Existence of entire solutions for a class of variable exponent elliptic equations. J. Differ. Equ. 257, 1529–1566 (2014)

    MathSciNet  MATH  Google Scholar 

  24. Fiscella, A., Pucci, P., Saldi, S.: Existence of entire solutions for Schrödinger-Hardy systems involving two fractional operators. Nonlinear Anal. 158, 109–131 (2017)

    MathSciNet  MATH  Google Scholar 

  25. Saintier, N., Silva, A.: Local existence conditions for an equations involving the \(p(x)\)-Laplacian with critical exponent in \(\mathbb{R} ^{N}\). Nonlinear Differ. Equ. Appl. 24, 19 (2017)

    MATH  Google Scholar 

  26. Alves, C.O., Ferreira, M.C.: Nonlinear perturbations of a \(p(x)\)-Laplacian equation with critical growth in \(\mathbb{R}^{N}\). Math. Nachr. 287, 849–868 (2014)

    MathSciNet  MATH  Google Scholar 

  27. Alves, C.O., Ferreira, M.C.: Multi-bump solutions for a class of quasilinear problems involving variable exponents. Ann. Mat. 194, 1563–1593 (2015)

    MathSciNet  MATH  Google Scholar 

  28. Alves, C.O., Ferreira, M.C.: Existence of solutions for a class of \(p(x)\)-Laplacian equations involving a concave-convex nonlinearity with critical growth in \(\mathbb{R}^{N}\). Topol. Methods Nonlinear Anal. 45, 399–422 (2015)

    MathSciNet  MATH  Google Scholar 

  29. Cammaroto, F., Vilasi, L.: On a perturbed \(p(x)\)-Laplacian problem in bounded and unbounded domains. J. Math. Anal. Appl. 402, 71–83 (2013)

    MathSciNet  MATH  Google Scholar 

  30. Dai, G.W.: Infinitely many solutions for a \(p(x)\)-Laplacian equation in \(\mathbb{R}^{N}\). Nonlinear Anal. 71, 1133–1139 (2009)

    MathSciNet  MATH  Google Scholar 

  31. Ge, B., Zhou, Q.M.: Existence and multiplicity of solutions for \(p(x)\)-Laplacian equations in \(\mathbb{R}^{N}\). Electron. J. Differ. Equ. 133, 1 (2014)

    Google Scholar 

  32. Fan, X.L., Han, X.Y.: Existence and multiplicity of solutions for \(p(x)\)-Laplacian equations in \(\mathbb{R}^{N}\). Nonlinear Anal. 59, 173–188 (2004)

    MathSciNet  MATH  Google Scholar 

  33. Fu, Y.Q., Zhang, X.: A multiplicity results for \(p(x)\)-Laplacian problem in \(\mathbb{R}^{N}\). Nonlinear Anal. 70, 2261–2269 (2009)

    MathSciNet  MATH  Google Scholar 

  34. Anello, G.: On the multiplicity of critical points for parameterized functionals on reflexive Banach spaces. Preprint (2012)

  35. Liu, X.Q., Liu, J.Q., Wang, Z.Q.: Quasilinear elliptic equations via perturbation method. Proc. Am. Math. Soc. 141, 253–263 (2013)

    MathSciNet  MATH  Google Scholar 

  36. Jeanjean, L.: On the existence of bounded Palais-Smale sequences and application to a Landesman-Lazer type problem set on \(\mathbb{R}^{N}\). Proc. R. Soc. Edinb. 129, 787–809 (1999)

    MATH  Google Scholar 

  37. Tang, X.H.: Infinitely many solutions for semilinear Schrodinger equations with sign-changing potential and nonlinearity. J. Math. Anal. Appl. 401, 407–415 (2013)

    MathSciNet  MATH  Google Scholar 

  38. Edmunds, D., Rakosnik, J.: Sobolev embedding with variable exponent. Stud. Math. 143, 267–293 (2000)

    MathSciNet  MATH  Google Scholar 

  39. Fan, X.L., Zhao, D.: On the spaces \(L^{p(x)}(\varOmega )\) and \(W^{m,p(x)}(\varOmega )\). J. Math. Anal. Appl. 263, 424–446 (2001)

    MathSciNet  Google Scholar 

  40. Fan, X.L., Han, X.: Existence and multiplicity of solutions for \(p(x)\)-Laplacian equations in \(\mathbb{R}^{N}\). Nonlinear Anal. 59, 173–188 (2004)

    MathSciNet  MATH  Google Scholar 

  41. Fan, X.L., Zhao, Y.Z., Zhao, D.: Compact imbedding theorems with symmetry of Strauss-Lions type for the space \(W^{1,p(x)}(\varOmega )\). J. Math. Anal. Appl. 255, 333–348 (2001)

    MathSciNet  MATH  Google Scholar 

  42. Lions, P.L.: The concentration-compactness principle in the calculus of variations, the locally compact case. Ann. Inst. Henri Poincaré, Anal. Non Linéaire 1, 109–145 (1984)

    MathSciNet  MATH  Google Scholar 

  43. Ambrosetti, A., Rabinowitz, P.: Dual variational methods in critical points theory and applications. J. Funct. Anal. 14, 349–381 (1973)

    MathSciNet  MATH  Google Scholar 

  44. Chabrowski, J., Fu, Y.: Existence of solutions for \(p(x)\)-Laplacian problems on a bounded domain. J. Math. Anal. Appl. 306, 604–618 (2005)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Harbin Engineering University, Harbin, 150001, P.R. China

    Bin Ge & De-Jing Lv

Authors
  1. Bin Ge
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. De-Jing Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bin Ge.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work is supported by the National Natural Science Foundation of China (No. U1706227, 11201095), the Fundamental Research Funds for the Central Universities (2019), the Postdoctoral research startup foundation of Heilongjiang (No. LBH-Q14044), the Science Research Funds for Overseas Returned Chinese Scholars of Heilongjiang Province (No. LC201502).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ge, B., Lv, DJ. Superlinear Elliptic Equations with Variable Exponent via Perturbation Method. Acta Appl Math 166, 85–109 (2020). https://doi.org/10.1007/s10440-019-00256-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10440-019-00256-2

Keywords

Mathematics Subject Classification

Search

Navigation