Abstract
Bicycling is the leading cause of sports-related traumatic brain injury. Most of the current bike helmets are made of expanded polystyrene (EPS) foam and ultimately designed to prevent blunt trauma, e.g., skull fracture. However, these helmets have limited effectiveness in preventing brain injuries. With the availability of high-rate micro-electrical-mechanical systems sensors and high energy density batteries, a new class of helmets, i.e., expandable helmets, can sense an impending collision and expand to protect the head. By allowing softer liner medium and larger helmet sizes, this novel approach in helmet design provides the opportunity to achieve much lower acceleration levels during collision and may reduce the risk of brain injury. In this study, we first develop theoretical frameworks to investigate impact dynamics of current EPS helmets and airbag helmets—as a form of expandable helmet design. We compared our theoretical models with anthropomorphic test dummy drop test experiments. Peak accelerations obtained from these experiments with airbag helmets achieve up to an 8-fold reduction in the risk of concussion compared to standard EPS helmets. Furthermore, we construct an optimization framework for airbag helmets to minimize concussion and severe head injury risks at different impact velocities, while avoiding excessive deformation and bottoming-out. An optimized airbag helmet with 0.12 m thickness at 72 ± 8 kPa reduces the head injury criterion (HIC) value to 190 ± 25 at 6.2 m/s head impact velocity compared to a HIC of 1300 with a standard EPS helmet. Based on a correlation with previously reported HIC values in the literature, this airbag helmet design substantially reduces the risks of severe head injury up to 9 m/s.






Similar content being viewed by others
References
Bambach, M. R., R. Mitchell, R. H. Grzebieta, and J. Olivier. The effectiveness of helmets in bicycle collisions with motor vehicles: A case–control study. Accid. Anal. Prev. 53:78–88, 2013.
Bourdet, N., C. Deck, R. P. Carreira, and R. Willinger. Head impact conditions in the case of cyclist falls. Proc. Inst. Mech. Eng. Part P 226:282–289, 2012.
Camacho, D. L., R. W. Nightingale, and B. S. Myers. The influence of surface padding properties on head and neck injury risk. J. Biomech. Eng. 123:432–439, 2001.
Camarillo, D., P. Shull, and J. Mattson. An instrumented mouthguard for measuring linear and angular head impact kinematics in American football. Ann. Biomed. Eng. 41:1939–1949, 2013.
Cheng, Z., W. Pilkey, J. Crandall, C. Bass, and K. Darvish. Limiting Performance of Helmets for the Prevention of Head Injury. Shock Vib. 6:299–320, 1999.
Cripton, P. A., D. M. Dressler, C. A. Stuart, C. R. Dennison, and D. Richards. Bicycle helmets are highly effective at preventing head injury during head impact: Head-form accelerations and injury criteria for helmeted and unhelmeted impacts. Accid. Anal. Prev. 70:1–7, 2014.
Croop, B., H. Lobo, and N. DatapointLabs. Selecting material models for the simulation of foams in ls-dyna. Proc. 7th Eur. LS-DYNA conference, Dynamore Gmbh, Salzburg, 2009.
Curnow, W. J. The efficacy of bicycle helmets against brain injury. Accid. Anal. Prev. 35:287–292, 2003.
de Geus, B., G. Vandenbulcke, L. Int Panis, I. Thomas, B. Degraeuwe, E. Cumps, J. Aertsens, R. Torfs, and R. Meeusen. A prospective cohort study on minor accidents involving commuter cyclists in Belgium. Accid. Anal. Prev. 45:683–93, 2012.
De Vries, D. Characterization of polymeric foams. Eindhoven University of Technology , 2009.
Do, S. and O. D. Weck. A personal airbag system for the Orion Crew Exploration Vehicle. Acta Astronaut. 81:239–255, 2012.
Eilert-Petersson, E. and L. Schelp. An epidemiological study of bicycle-related injuries. Accid. Anal. Prev. 29:363–372, 1997.
Esgar, J. B. and W. C. Morgan. Analytical study of soft landings on gas-filled bags. NASA , 1960.
Faul, M., L. Xu, M. M. Wald, and V. Coronado. Traumatic brain injury in the united states. Atlanta, GA: Centers for Disease Control and Prevention, National Center for Injury Prevention and Control , 2010.
Federal Motor Vehicle Safety Standards (FMVSS). 571.202a. Section 571, Standard 202a-Head restraints.
Finnoff, J. T., E. R. Laskowski, K. L. Altman, and N. N. Diehl. Barriers to bicycle helmet use. Pediatrics 108:e4, 2001.
Folksam. Bicycle Helmet Test. Technical report, 2015.
Funk, J. R., S. Rowson, R. W. Daniel, and S. M. Duma. Validation of concussion risk curves for collegiate football players derived from hits data. Ann. Biomed. Eng. 40:79–89, 2012.
Hansen, K., N. Dau, F. Feist, C. Deck, R. Willinger, S. M. Madey, and M. Bottlang. Angular impact mitigation system for bicycle helmets to reduce head acceleration and risk of traumatic brain injury. Accid. Anal. Prev. 59:109–117, 2013.
Healy, D. G. Head injuries in sport. ABC of Sports and Exercise Medicine p. 10, 2015.
Hernandez, F., L. C. Wu, M. C. Yip, K. Laksari, A. R. Hoffman, J. R. Lopez, G. A. Grant, S. Kleiven, and D. B. Camarillo. Six degree-of-freedom measurements of human mild traumatic brain injury. Ann. Biomed. Eng. pp. 1–17, 2014.
Hertz, E. A note on the head injury criterion (hic) as a predictor of the risk of skull fracture. Ann. Adv. Automot. Med. 37:303–312, 1993.
Howland, J., J. Sargent, M. Weitzman, T. Mangione, R. Ebert, M. Mauceri, and M. Bond. Barriers to bicycle helmet use among children: results of focus groups with fourth, fifth, and sixth graders. Am. J. Dis. Child. 143:741–744, 1989.
Juhra, C., B. Wieskötter, K. Chu, L. Trost, U. Weiss, M. Messerschmidt, A. Malczyk, M. Heckwolf, and M. Raschke. Bicycle accidents–do we only see the tip of the iceberg?: A prospective multi-centre study in a large german city combining medical and police data. Injury 43:2026–2034, 2012.
Kleiven, S. Why most traumatic brain injuries are not caused by linear acceleration but skull fractures are. Front. Bioeng. Biotechnol. 1, 2013.
Kurt, M., J. Sganga, and D. B. Camarillo. Hybrid Helmet,U.S. Provisional Patent Application. 62/141,675 , 2015.
Laksari, K., L. C. Wu, M. Kurt, C. Kuo, and D. C. Camarillo. Resonance of human brain under head acceleration. J. R. Soc. Interface 12:20150331, 2015.
Lamb, L. and T. Hoshizaki. Deformation mechanisms and impact attenuation characteristics of thin-walled collapsible air chambers used in head protection. Proc. Inst. Mech. Eng. Part H 223:1021–1031, 2009.
Maimaris, C., C. Summer, C. Browning, and C. Palmer. Injury patterns in cyclists attending an accident and emergency department: a comparison of helmet wearers and non-wearers. BMJ 308:1537–1540, 1994.
Marieb, E. N. and K. Hoehn. Human Anatomy & Physiology, Pearson Education,2007 .
Mertz, H. J., P. Prasad, and A. L. Irwin. Injury risk curves for children and adults in frontal and rear collisions. Technical report, SAE Technical Paper, 1997.
Mills, N. and A. Gilchrist. Finite-element analysis of bicycle helmet oblique impacts. Int. J. Impact Eng. 35:1087–1101, 2008.
Mills, N. J. and A. Gilchrist. Bicycle helmet design. Proc. Inst. Mech. Eng. Part L 220:167–180, 2006.
Moss, W. C. and M. J. King. Impact response of US Army and National Football League helmet pad systems. Technical report, 2011.
Moss, W. C., M. J. King, and E. G. Blackman. Towards reducing impact-induced brain injury: lessons from a computational study of army and football helmet pads. Comput. Methods Biomech. Biomed. Eng. 17:1173–1184, 2014.
Nagurka, M. and S. Huang. A mass-spring-damper model of a bouncing ball. Am. Control Conf. , Vol. 1, pp. 499–504, IEEE, 2004.
Newman, J. A. Biomechanics of head trauma: head protection, pp. 303–323, Springer,2002.
Ogden, R. Large deformation isotropic elasticity-on the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A 326:565–584, 1972.
Ozturk, U. E. and G. Anlas. Finite element analysis of expanded polystyrene foam under multiple compressive loading and unloading. Mater. Des. 32:773–780, 2011.
Paquette, S., C. Gordon, and B. Bradtmiller. Anthropometric survey (ansur) ii pilot study: methods and summary statistics. Technical report, DTIC Document, 2009.
Pellman, E. J., D. C. Viano, A. M. Tucker, I. R. Casson, and J. F. Waeckerle. Concussion in professional football: reconstruction of game impacts and injuries. Neurosurgery 53:799–814, 2003.
Ramon, O. and J. Miltz. Prediction of dynamic properties of plastic foams from constant–strain rate measurements. J. Appl. Polym. Sci. 40:1683–1692, 1990.
Thompson, R. S., F. P. Rivara, and D. C. Thompson. A case-control study of the effectiveness of bicycle safety helmets. N. Engl. J . Med. 320:1361–1367, 1989.
United States Consumer Product Safety Commision (CPSC). Safety Standard for Bicycle Helmets: Final Rule. Technical report, 1998.
United States Consumer Product Safety Commision (CPSC). Head Injury-Related Deaths to Children Under 15 Years Old, Calendar Years, 1991–2000. Technical report, 2003.
Yoganandan, N., F. A. Pintar, J. Zhang, and J. L. Baisden. Physical properties of the human head: mass, center of gravity and moment of inertia. J. Biomech. 42:1177–1192, 2009.
Zhang, J., N. Kikuchi, V. Li, A. Yee, and G. Nusholtz. Constitutive modeling of polymeric foam material subjected to dynamic crash loading. Int. J. Impact Eng. 21:369–386, 1998.
Zhang, L., K. H. Yang, and A. I. King. A Proposed Injury Threshold for Mild Traumatic Brain Injury. J. Biomech. Eng. 126:226–236, 2004.
Acknowledgments
The study was supported by the National Institutes of Health (NIH) National Institute of Biomedical Imaging and Bioengineering (NIBIB) 3R21EB01761101S1, Thrasher Research Fund, David and Lucile Packard Foundation 38454, Child Health Research Institute Transdisciplinary Initiatives Program, and NIH UL1 TR000093 for biostatistics consultation. Dr. Kurt is the recipient of the Thrasher Research Fund Early Career Award. A provisional patent application has been filed for a helmet design using the optimization strategy described in this paper and will be assigned to Stanford University.26 Royalties gained from any intellectual property granted for this work will be shared among the inventors, the department, and the school, according to Stanfords technology licensing policies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Associate Editor Stefan M. Duma oversaw the review of this article.
Appendix
Appendix
Helmet Impact Dynamics Modeling
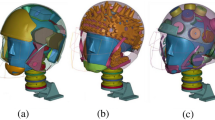
The geometry we assume for the helmets is hemispherical shells, as shown in Fig. 7. In making the analysis, the following general assumptions are made for helmet dynamics:
-
(1)
The head and the helmet are coupled rigidly.
-
(2)
The head & helmet system is only moving in the vertical direction.
-
(3)
The normal vector of the contact area is always in the impact direction.
Airbag Impact Dynamics Modeling
In modeling the airbag impact dynamics, the following assumptons are made:
-
(1)
Air behaves like an ideal gas at the given conditions.
-
(2)
The airbag is flexible but inelastic.
-
(3)
Friction and the bending resistance of the airbag fabric are neglected.
-
(4)
The mass of the air is negligible.
The most general form of the equations of motion for a hemispherical airbag helmet is as follows:
where x represents the instanteous distance between the center of gravity (CoG) of the head and the ground, m is the total system mass, P(x) and A(x) are instantenous pressure and contact area values of the airbag and \(P_{atm}\) is atmospheric pressure. The physical constraint to the system depicted in (1) is
where \(d_{head}\) is the vertical distance of the CoG of the head to the helmet and \(d_{helmet}\) is the thickness of the helmet.
We assume a hemispherical geometry for the airbag helmet. We assume that the helmet would completely flatten out if it reached to the deformation limit. This indeed can not happen for Fig. 7 since the deformation is limited up to the skull. By using simple geometric relations, the contact area of the airbag helmet can be formulated as follows:
Note that this contact area can be adjusted with a scaling factor when the actual contact between the surface and the helmet is limited, especially in the case of complex geometries.
The initial volume of the airbag helmet is
Using (3) and (4), we find the instantenous volume of the airbag as a function of x
By using the assumption of ideal gas, we can find the instantenous pressure of the airbag helmet during the impact by simply equating P(x) V(x) with \(P_i V_i\)(initial conditions)
EPS Helmet Impact Dynamics Modeling
To model the impact dynamics of EPS helmets, we assume the same hemispherical shell geometry. The contact area of the EPS helmet is assumed to be of the form given in (3). The equation of motion for the EPS helmet is as follows:
where x represents the instantaneous distance between the center of gravity (CoG) of the head and the ground, m is the total system mass, \({\sigma _{EPS}}(\frac{x}{{{d_{helmet}}}})\) is the loading/unloading stress-strain curve depicted in Fig. 2a and A(x) is the instantenous contact area between the EPS helmet and the ground. The effective damping coefficient \(c_{EPS}\) was calculated by using relations for a bouncing elastic body on a rigid surface:36
where m is the total system mass, \(\Delta T\) represents the contact duration and \(\varepsilon \) corresponds to coefficient of restitution. In order to find \(c_{EPS}\), we need to solve for the coefficient of restitution, which is an implicit function of \(\Delta T\) as follows
where n is the number of bounces that the elastic body experiences and \(h_{0}\) is the height from which the head is dropped. We assume n to be 2 and \(\Delta T \) to be 10 ms based on our experimental observations.
Summary of Helmet Dynamics Parameters
We give an overview of the values of mass, helmet size and other critical parameters used for modeling helmet dynamics (Table 1).
Ogden Material Modeling
We use Ogden rubber material model that is widely used for modeling foams.38 Assuming a zero lateral stress and zero Poisson’s ratio, we can formulate the material stress as follows
where \(\lambda \) is defined as the stretch ratio (i.e., the ratio between the final helmet thickness to the initial helmet thickness) and α, β and μ are material constants.
We use the first order approximation of (10) to model polymeric foams. The equation reduces to the following form
For EPS20, the Ogden material parameters are given below in the table for the first-order approximation Table 2.
For ideal foam optimization in Fig. 5a, the limits we used for the above parameters are as follows
These limits lead to a semi-constrained optimization and give the opportunity to minimize peak accelerations at varying helmet sizes, as shown in Fig. 5a.
ATD Rfor Different Impact Orientations
Below, we represent the parietal and vertex experimental results for ATD tests, which were previously depicted in Fig. 3b and Table 3.
Hövding Geometry
Since Hövding is a relatively new product, its geometry is not well-known. Therefore, we show top, side and front views of Hövding in an inflated state in Fig. 8.
Rights and permissions
About this article
Cite this article
Kurt, M., Laksari, K., Kuo, C. et al. Modeling and Optimization of Airbag Helmets for Preventing Head Injuries in Bicycling. Ann Biomed Eng 45, 1148–1160 (2017). https://doi.org/10.1007/s10439-016-1732-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10439-016-1732-1