Skip to main content
SpringerLink
Log in

Snap-through of an elastica under bilateral displacement control at a material point

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

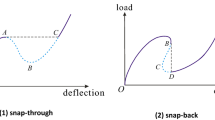
Snap-through phenomenon widely occurs for elastic systems, where the systems lose stability at critical points. Here snap-through of an elastica under bilateral displacement control at a material point is studied, by regarding the whole elastica as two components, i.e., pinned-clamped elasticas. Specifically, stiffness−curvature curves of two pinned-clamped elasticas are firstly efficiently located based on the second-order mode, which are used to determine the shapes of two components. Similar transformations are used to assemble two components together to form the whole elastica, which reveals four kinds of shapes. One advantage of this way compared with other methods such as the shooting method is that multiple coexisting solutions can be located accurately. On the load−deflection curves, four branches correspond to four kinds of shapes and first two branches are symmetrical to the last two branches relative to the original point. For the bilateral displacement control, the critical points can only appear at saddle-node bifurcations, which is different to that for the unilateral displacement control. Specifically, one critical point is found on the first branch and two critical points are found on the secondary branch. In addition, the snap-through among different branches can be well explained with these critical points.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Holmes, D.P., Crosby, A.J.: Snapping surfaces. Adv. Mater. 19, 3589–3593 (2007)

    Article  Google Scholar 

  2. Forterre, Y., Skotheim, J.M., Dumais, J., et al.: How the venus flytrap snaps. Nature 433, 421–425 (2005)

    Article  Google Scholar 

  3. Forterre, Y.: Slow, fast and furious: understanding the physics of plant movements. J. Exp. Bot. 64, 4745–4760 (2013)

    Article  Google Scholar 

  4. Bowen, C.R., Kim, H.A., Weaver, P.M., et al.: Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ. Sci. 7, 25–44 (2014)

    Article  Google Scholar 

  5. Scarselli, G., Nicassio, F., Pinto, F., et al.: A novel bistable energy harvesting concept. Smart Mater. Struct. 25, 055001 (2016)

    Article  Google Scholar 

  6. Shan, S., Kang, S.H., Raney, J.R., et al.: Multistable architected materials for trapping elastic strain energy. Adv. Mater. 27, 4296–4301 (2015)

    Article  Google Scholar 

  7. Chen, T., Mueller, J., Shea, K.: Integrated design and simulation of tunable, multi-state structures fabricated monolithically with multi-material 3D printing. Sci. Rep. 7, 45671 (2017)

    Article  Google Scholar 

  8. Haghpanah, B., Salari-Sharif, L., Pourrajab, P., et al.: Multistable shape-reconfigurable architected materials. Adv. Mater. 28, 7915–7920 (2016)

    Article  Google Scholar 

  9. Li, H., Liang, X.Y., Song, W.B.: Buckling-controlled two-way shape memory effect in a ring-shaped bilayer. Acta Mech. Sin. 35, 1217–1225 (2019)

    Article  Google Scholar 

  10. Hu, N., Burgueno, R.: Buckling-induced smart applications: recent advances and trends. Smart Mater. Struct. 24, 063001 (2015)

    Article  Google Scholar 

  11. Kochmann, D.M., Bertoldi, K.: Exploiting microstructural instabilities in solids and structures: from metamaterials to structural transitions. Appl. Mech. Rev. 69, 050801 (2017)

    Article  Google Scholar 

  12. Zhang, X.W., Yang, J.L.: Inverse problem of elastica of a variable-arc-length beam subjected to a concentrated load. Acta Mech. Sin. 21, 444–450 (2005)

    Article  MathSciNet  Google Scholar 

  13. Seide, P.: Large deflections of a simply supported beam subjected to moment at one end. ASME J. Appl. Mech. 51, 519–525 (1984)

    Article  Google Scholar 

  14. Phungpaingam, B., Chucheepsakul, S.: Postbuckling of elastic beam subjected to a concentrated moment within the span length of beam. Acta Mech. Sin. 23, 287–296 (2007)

    Article  Google Scholar 

  15. Harvey, P.S., Virgin, L.N.: Coexisting equilibria and stability of a shallow arch: unilateral displacement control experiments and theory. Int. J. Solids Struct. 54, 1–11 (2015)

    Article  Google Scholar 

  16. Gomez, M., Moulton, D.E., Vella, D.: Critical slowing down in purely elastic snap-through instabilities. Nat. Phys. 13, 142–145 (2016)

    Article  Google Scholar 

  17. Deng, H., Cheng, L., Liang, X., et al.: Topology optimization for energy dissipation design of lattice structures through snap-through behavior. Comput. Methods Appl. Mech. Eng. 358, 112641 (2020)

    Article  MathSciNet  Google Scholar 

  18. Plaut, R.H., Virgin, L.N.: Vibration and snap-through of bent elastica strips subjected to end rotations. ASME J. Appl. Mech. 76, 041011 (2009)

    Article  Google Scholar 

  19. Chen, J.S., Hung, S.Y.: Snapping of an elastica under various loading mechanisms. Eur. J. Mech. A 30, 525–531 (2011)

    Article  Google Scholar 

  20. Chen, J.S., Ro, W.C.: Deformations and stability of an elastica subjected to an off-axis point constraint. ASME J. Appl. Mech. 77, 031006 (2010)

    Article  Google Scholar 

  21. Chen, J.S., Wu, H.H.: Deformation and stability of an elastica under a point force and constrained by a flat surface. Int. J. Mech. Sci. 53, 42–50 (2011)

    Article  Google Scholar 

  22. Domokos, G., Holmes, P., Royce, B.: Constrained euler buckling. J. Nonlinear. Sci. 7, 281–314 (1997)

    Article  MathSciNet  Google Scholar 

  23. Wang, C.M., Lam, K.Y., He, X.Q., et al.: Large deflections of an end supported beam subjected to a point load. Int. J. Non-Linear Mech. 32, 63–72 (1997)

    Article  Google Scholar 

  24. Plaut, R.H.: Snap-through of arches and buckled beams under unilateral displacement control. Int. J. Solids Struct. 63, 109–113 (2015)

    Article  Google Scholar 

  25. Hartono, W.: Discussion: elastica of simple variable-arc-length beam subjected to end moment. ASCE J. Eng. Mech. 123, 92–95 (1997)

    Article  Google Scholar 

  26. Cao, D., Gao, Y., Hu, W.: Modeling and power performance improvement of a piezoelectric energy harvester for low-frequency vibration environments. Acta Mech. Sin. 35, 894–911 (2019)

    Article  MathSciNet  Google Scholar 

  27. Yu, L., Tang, L., Yang, T.: Experimental investigation of a passive self-tuning resonator based on a beam-slider structure. Acta Mech. Sin. 35, 1079–1092 (2019)

    Article  Google Scholar 

  28. Fang, F., Xia, G., Wang, J.: Nonlinear dynamic analysis of cantilevered piezoelectric energy harvesters under simultaneous parametric and external excitations. Acta Mech. Sin. 34, 561–577 (2018)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants 91648101 and 11972290) and the Innovation Foundation for Doctor Dissertation of Northwestern Polytechnical University (Grant CX201811), as well as the Fundamental Research Funds for the Central Universities (Grant 3102018zy012).

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Northwestern Polytechnical University, Xi’an, 710072, China

    Q. Wang, H. L. Zou & Z. C. Deng

Authors
  1. Q. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. L. Zou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Z. C. Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Z. C. Deng.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Q., Zou, H.L. & Deng, Z.C. Snap-through of an elastica under bilateral displacement control at a material point. Acta Mech. Sin. 36, 727–734 (2020). https://doi.org/10.1007/s10409-020-00937-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-020-00937-4

Keywords

Search

Navigation